Complete Solutions to Example of chapter CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| SL ARORA | Example |
| Number Of Questions | 96 |
| Academic Year | 2023-24 |
`10^(20)` electrons, each having a charge of `1.6xx10^(-19) C, pass from a point A towards another point B in 0.1 s. What is the current in ampere ? What is its direction ?
View SolutionShow that one ampere is equivalent to flow of `6.25xx10^(-18)` elementary electrons per second ? Charge on electron `=1.6 xx 10^(-19)C`.
View SolutionHow many electrons pass through a lamp in one minute, if the current is 300 mA ?
View SolutionHow many electrons per second flow through a filament of a 120 V and 60 W electric bulb ?
View SolutionIn Bohr model of hydrogen atom , the electron revolves around the nucleus in a circular orbit of radius `5.1 xx 10^(-11)m` at a frequency of `6.8 xx 10^(15)` revolutions per second. Find the equivalent current at may point on the orbit of the electron
View SolutionIn Bohr model of hydrogen atom, the electron revolves around the nucleus in a circular orbit of radius `5.0xx10^(-11)` m with a speed `2.2 xx10^(6) ms^(-1)`. Find the equivalnet current. (Electronic charege = `1.6 xx 10^(-19)`coulomb)
View SolutionAn electron beam has an aperture of `1.0 mm^(2)`. A total of `6xx10^(16)` electrons flow through any perpendicular cross-section per second. Calculate (i) the current (ii) the current density in the electron beam.
View SolutionThe earth's surface has a negative surface charge density of `10^(-9) Cm^(-2)` . The potential difference of 400 kV between the top of the atmosphere and the surface results (due to low conductivity of the lower atmosphere) in a current of only 1800 A over the entire globe. If there were no mechanism of sustaining atmosphereic electric field , how much time (roughly) would be required to neutralise the earth's surface ? (This never happens in practice because there is a mechanism to replenish electric charges namely the continual thunder storms and lightning in different parts of the globe). Radius of the earth `= 6.37 xx 10^(6) m`.
View SolutionThe amount of charge passed in time t through a cross-section of a wire is
`Q(t)=At^(2)+Bt+C.`
(a)Write the dimensional formulae for A,B and C.
(b) If the numerical values of A,B,and C are 5,3 and 1 respectively in SI units,find the value of the current at t=5 s.
View SolutionIn a discharge tube, the number of hydrogen ions (i.e., protons) drifting across a cross-section per second is `1.0xx10^(18)`, while the number of electrons drifting in the opposite direction across another cross-section is `2.7xx10^(18)` per second. If the supply voltage is 230 V, what is the effective resistance of the tube ?
View SolutionThe current flowing through a conductor is 2 mA at 50 V and 3 mA at 60 v. Is it an ohmic or non-ohmic conductor ?
View SolutionA uniform wire is cut into 10 segments increasing in length in equal steps, the resitance of the shortest segment is R and the resistances of the other segments increase in steps of `8 Omega`. If the resistance of the longest segment is 2R, find the value of R and hence find the resistance of the original wire.
View SolutionA current of 2 mA is passed through a colour coded carbon resistor with first, second and third rings of yellow, green and orange colours. What is the voltage drop across the resistor ?
View SolutionAn are lamp operates at 80 V, 10 A. Suggest a method to use it with a 240 V d.c. source. Calculate the value of the electric component required for this purpose.
View SolutionCalculate the resistivity of a material of a wire 10 m long, 0.4 mm in diameter and having a resistance of `2.0 Omega`.
View SolutionThe external diameter of a 5 metre long hollow tube is 10 cm and the thickness of its wall is 5 mm. If the specific resistance of copper be `1.7xx10^(5)` ohm-metre, then determine its resistance.
View SolutionCalculate the electrical conductivity of the material of a conductor of length 3 m, area of cross-section `0.02 mm^(2)` having a resistance of `2 Omega`.
View SolutionWhat length of a copper wire of cross-sectional area `0.01 mm^(2)` would be required to obtain a resistance of `1k Omega`? Resistivity of copper `=1.7xx10^(-8) Omega m`.
View SolutionA wire has a length of 2.0 m and a resistance of `5.0 Omega`. Find the electric field existing inside the wire if it carries a current of 10 A.
View SolutionA copper wire of radius 0.1 mm and resistance `1 k Omega` is connected across a power supply of 20 V. (i) How many electrons are transferred per second between the supply and the wire at one end ? (ii) Write down the current density in the wire.
View SolutionFind the resistivity of eureka wire 1.1 m long and 0.2 mm in diameter. Resistivity of eureka `=49xx10^(-8) Omega`m. What is the current flowing through this wire when a potential difference of 2 V is applied across it ?
View SolutionA wire of resistance `10 Omega` is drawn out so that its length is thrice its original length. Calculate its new resistance (resistivity and density of the material remain uncharged).
`" "` Or
A wire of resistance `10 Omega` is drawn out so that its length is increased by twice its original length. Calculate its new resistance.
View SolutionA wire has a resistance of `16 Omega`. It is melted and drawn into a wire of half its length. Calculate the resistance of the new wire. What is the percentage change in its resistance ?
View SolutionTwo wires of the same material having lengths in the ratio `1 : 2` and diameters in the ratio `2 : 3` are connected in series with an accumulator. Compute the ratio of P.D. across the two wires.
View SolutionTwo wires A and B equal mass and of the same metal are taken. The diameter of the wire A is half the diameter of wire B. If the resistance of wire A is `24 Omega`, calculatate the resistance of wire B.
View SolutionA piece of silver ahs a resistance of `1 Omega`. What will be the resistance of a constantan wire of one-third length and one-half diameter, if the specific resistance of constantan is 30 times that of silver ?
View SolutionTwo wires of equal length, one of aluminium and the other of copper have the same resistance. Which of the two wires is lighter ? Hence explain why aluminium wires are prefered for overhead power cables ? Given `rho Al=2.63xx10^(-8) Omega m rho Cu=0.72xx10^(-8) Omega m` , relative density of Al=2.7 and that of Cu =8.9.
View SolutionTwo wires A and B are of same metal, have the same area of cross-section and have their lengths in the ratio `2 : 1`. What will be the ratio of currents flowing through them respectively when the same potential difference is applied across the length of each of them ?
View SolutionOn applying the same potential difference between the ends of wires of iron and copper of the same length, the same current flows in them. Compare their radii. Specific resistances of iron and copper are respectively `1.0xx10^(-7)` and `1.6xx10^(-8) Omega m`. Can their current-densities be made equal by taking appropriate radii ?
View SolutionA wire of resistance `4 Omega` is used to wind a coil of radius 7 cm. The wire has a diameter of 1.4 mm and the specific resistance of its material is `2xx10^(-7) Omega m`. Find the number of turns in the coil.
View SolutionA current of 5 ampere is passing through a metallic wire of cross-sectional area `4xx10^(-6) m^(2)`. If the density of the charge-carriers in the wire is `5xx10^(26) m^(-3)`, find the drift speed of the electrons.
View SolutionA copper wire has a resistance of `10 Omega ` and an area of cross-section `1 mm^(2)`. A poetential difference of 10 V exists across the wire. Calculate the drift speed of electrons if the number of electrons per cubic metre in copper is `8xx10^(28)` electrons.
View SolutionThe number density of conduction electrons in a copper conductor is `8.5xx10^(28) m^(-3)`. How long does an electron take to drift from one end of a wire 3.0 m long to its other end ? The area of cross-section of the wire is `2.0xx10^(-6) m^(2)` and it is carrying a current of 3.0 A.
View SolutionCalculate the average drift speed of conduction electrons in a copper wire of cross-sectional area `1.0xx10^(-7)m^(2)`, carrying a current of 1.5 A. Assume that each copper atom contributes roughly one conduction electron. The density of copper is `9.0xx10^(3) kg m^(-3)` and its atomic mass is 63.5. Take Avogadro's number `=6.0xx10^(23)`.
View SolutionThe resistivity of copper at room temperatrue is `1.7xx10^(-8) Omega m`. If the free electron density of copper is `8.4xx10^(28) m^(-3)`, find the relaxation time for the free electrons of copper. Given `m_(e)=9.11xx10^(-31) kg ` and `e=1.6xx10^(-19) C`.
View SolutionAn aluminium wire of diameter 0.24 cm is connected in series to a copper wire of diameter 0.16 cm. The wires carry an electric current of 10 ampere. Find (i) current-density in the aluminium wire (ii) drift velocity of electrons in the copper wire. Given : Number of electrons per cubic metre volume of copper `=8.4xx10^(28)`.
View SolutionAssuming that there is one free electron per atom in copper, determine the number of free electrons in `1 "metre"^(3)` volume of copper. Density of copper is `8.9xx10^(3) kgm^(-3)` and atomic weight 63.5. (Avogadro's number, `N=6.02xx10^(26)` per kg-atom).
View SolutionA current of 1.0 ampere is flowing through a copper wire of length 0.1 metre and cross-section `1.0xx10^(-6) m^(2)`. (i) If the specific resistance of copper be `1.7xx10^(-8) Omega m`, calculate the potential difference across the ends of the wire. (ii) Determine current density in the wire. (iii) If there be one free electron per atom in copper, then determine the drift velocity of electrons. Given : density of copper `=8.9xx10^(3) kg m^(-3)`, atomic weight`=63.5, N=6.02xx10^(26)` per kg-atom.
View SolutionA wire has a resistance of `2.1 Omega` at 300 K and a resistance of `2.7 Omega` at 373 K. Determine the temperature coefficent of resistance of the material.
View SolutionAt room temperature `(27^(@)C)`, the resistance of a heating element is `100 Omega`. What is the temperature of the element if the resistance is found to be `117 Omega`, given that temperature coefficient of the resistor material is `1.70xx10^(-4) .^(@)C^(-1)`.
View Solution(i) At what temperature would the resistance of a copper conductor be double its resistance at `0^(@)C` ?
(ii) Does this temperature hold for all copper conductors regardles of shape and size ? Given `alpha` for Cu`=3.9xx10^(-3) .^(@)C^(-1)`.
View SolutionA heating element using nichrome connected to a 230 V supply draws an initial current of 3.2 A which settles after a few seconds to a steady value of 2.8 A. What is the steady temperature of the heating element if the room temperature is `27^(@)C` ? Temperature coefficient of resistance of nichrome averaged over the temperature range involved is `1.70xx10^(-4) C^(-1)`.
View SolutionResistance of tungsten wire at `150^(@)C` is `133 Omega`. Its resistance temperature coefficient is `0.0045//^(@)C`. The resistance of this wire at `500^(@)C` will be
View SolutionThe rsistance of a conductor at `20^(@)C` is `3.15 Omega` and at `100^(@)C` is `3.75 Omega`. Determine the temperature coefficient of resistance of the conductor. What will be the resistance of the conductor at `0^(@)C` ?
View SolutionA standard coil marked `2 Omega` is found to have a resistance of `2.118 Omega " at " 30^(@)C`. Calculate the temperature at which the marking is correct. The temperature coefficient of the resistance of the material of the coil is `0.0042 .^(@)C^(-1)`.
View SolutionA poetential difference of 200 V is applied to a coil at a temperature of `15^(@)C` and the current is 10 A. What will be the mean temperature of the coil when the current hass fallen to 5 A, the applied voltage being same as before ? Given `alpha=(1)/(234).^(@)C^(-1) " at " 0^(@)C`.
View SolutionThe resistances of an iron wire and a copper wire at `20^(@)C`are `3.9(Omega)`and `4.1(Omega)`respectively. At what temperature will the resistances be equal?Temperature coefficient of resistivity for iron is `5.0xx10^(-3)K^(-1)`and for copper it is `4.0xx10^(-3)k^(-1).`Neglect any thermal expansion.
View SolutionThe current through a conductor is 1 ampere when the temperature is `0^(@)C` and 0.7 ampere when the temperature is `100^(@)C`. What would be current when the temperature of the conductor is `1200^(@)C` ?
View SolutionA carbon filament has a resistance of `100 Omega " at " 0^(@)C`. What must be the resistance of a copper filament placed in series with carbon so that the combination has the same resistance at all temperatures ? Temperature coefficient of resistance of carbon `=-0.0007 .^(@)C^(-1)` and that of copper is `0.004^(@)C^(-1)`.
View SolutionA metal wire of diameter 2 mm and length 100 m has a resistance of `0.5475 Omega " at " 20^(@)C` and `0.805 Omega " at " 150^(@)C`. Find (i) the temperature of coefficient of resistance (ii) resistance at `0^(@)C` (iii) resistivities at `0^(@)` and `20^(@)C`.
View SolutionGiven the resistance of `1 Omega, 2 Omega, 3 Omega`, how will you combine them to get an e3quivalent resistance of :
`(11)/(3) Omega " " (ii) (11)/(5) Omega " " (iii) 6 Omega " " (6)/(11) Omega` ?
View SolutionGiven n resistors each of resistane R, how will you combine them to get the (i) maximum, (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
View SolutionTwo square metal plates A and B are of same thickness and material. The side of B is twice that of A. These are connected in series, as shown in Fi. 4.3. Find the ratio `R_(A)//R_(B)` of the resistance of the two plates.
View SolutionThree conductors of conductances `G_(1), G_(2) " and " G_(3)` are connected in series. Find their equivalent conductance.
View SolutionA set of n identical resistors, each of resistance `R Omega`, when connected in series have an effective resistance `X Omega` and when the resistors are connected in parallel, their effective resistance is `Y Omega`. Find the relation between R, X and Y.
View SolutionA parallel combination of three resistors takes a current of 7.5 A from a 30 V supply. If the two resistors are `10 Omega " and " 12Omega`, find the third one.
View SolutionA wire of resistance 4 R is bent in the form of a circle [Fig 4.4]. What is the effective resistance between the ends of the diameter ?

View SolutionThe resistance of two conductors in series is `40 Omega` and their resistance becomes `7.5 Omega`, when coneected in parallel. Find the resistance of the individual conductors.
View SolutionA wire of uniform cross-section and length `l` has a resistance of `16 Omega ` is cut into four equal parts. Each part is stretched uniform to length `l` and all the four stretched parts are connected in parallel calcuate the total resistance of the combination so formed. Assume that stretching of wire does not cause any change in the density of its material
View SolutionA copper rod of length 20 cm and cross-sectional area `2 mm^(2)` is joined with a similar aluminium rod as shown in Fig. 4.6. Find the resistance of the combination between the ends. Resistivity of copper `=1.7xx10^(-8) Omega `m and resistivity of aluminium `=2.6xx10^(-8) Omega`m.

View SolutionFind the value of current I in the circuit
View SolutionA letter A consists of a uniform wire of resistance 1 ohm per cm. The sides of the letter are each 20 cm long and the cross-piece in the middle is 10 cm long while the apex angle is `60^(@)`. Find the resistance of the letter between the two ends of the legs.
View SolutionDetermine the voltage drop across the resistor `R_(1)` in the circuit given below with `E=60 V, R_(1)=18 Omega, R_(2)=10 Omega`.
View SolutionDetermine the equivalent resistance of the following net-works :

View Solution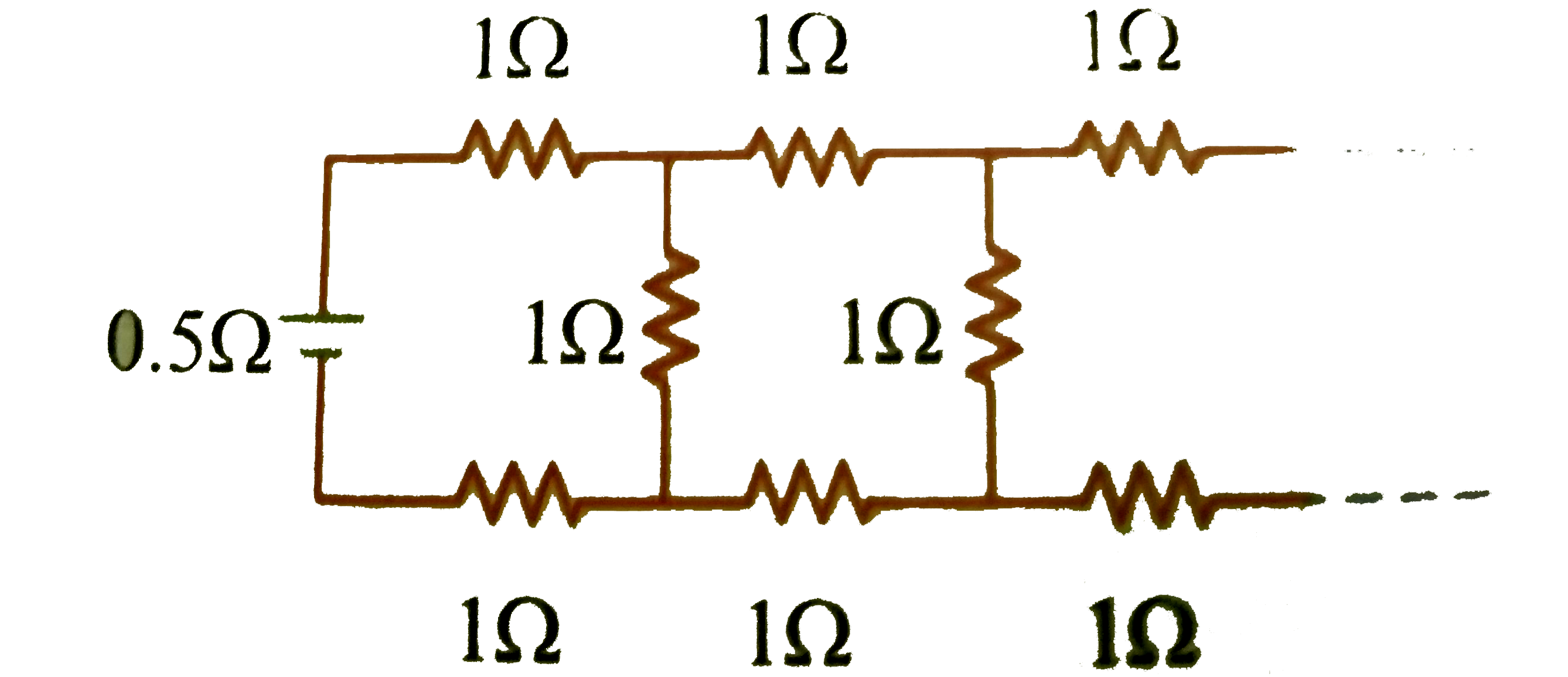
Determine the current drawn from a `12V` supply with internal resistance `0.5Omega`. By the infinite network shown in fig. Each resistor has `1Omega` resistance.
View SolutionFind the effective resistance between points A and B for the network
View SolutionFind the effective resistance of the network shown in Fig.4.15 between the points A and B when (i) the switch S is open (ii) switch S is closed.
View SolutionFind the equivalent resistance between the points A and B of the network of resistors shown in Fig. 4.16.
View SolutionFind the effective resistance between points A and B of the network of resistors
View SolutionIn the circuit shown in Fig. 4.19. `R_(1)=100 Omega, R_(2)=R_(3)=50 Omega, R_(4)=75 Omega` and E=4.75 V. Work out the equivalent resistance of the circuit and the current in each resistor.
View SolutionIn the circuit shown in Fig.4.20 both the ammeter and the cell have negligible resistance. Three external resistors are identical. When the switch S is opened, the ammeter reads 0.6 A. What will the ammeter read when the switch S is closed ?
View SolutionFor driving a current of 3 A for 5 minutes is an electric circuit, 900 J of work is to be done. Find the emf of the source in the circuit.
View SolutionA voltmeter of resistance `998 Omega` is connected across a cell of emf 2 V and internal resistance `2 Omega`. Find the p.d. across the voltmeter, that across the terminals of the cell and percentage error in the reading of the voltmeter.
View SolutionA secondary cell after long use has an emf of 1.9 V and a large internal resistance of `380 Omega`. What maximum current can be drawn from the cell ? Could the cell drive the starting motor of a car ?
View SolutionA battery of emf 10 v and internal resistane `3 Omega` is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistane of the resistors ? What is the terminal voltage of the battery when the circuit is closed ?
View SolutionIn the circuit shown in Fig. 4.25, the voltmeter reads 1.5 V, when the key is open. When the key is closed, the voltmeter reads 1.35 V and ammeter reads 1.5 A. Find the emf and the internal resistance of the cell.
View SolutionA battery of emf 3 volt and internal resistance r is connected in series with a resistor of `55 Omega` through an ammeter of resistance `1 Omega`. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View SolutionThe reading on a high resistance voltmeter when a cell is connected across it is 2.2 V. When the terminals of the cell are also connected to a resistance of `5 Omega`, the voltmeter reading drops to 1.8 V. Find the internal resistance of the cell.
View SolutionThe emf of a battery is 6 V and its internal resistance is `0.6 Omega`. A wire of resistance `2.4 Omega` is connected to the two ends of the battery, calculate (a) current in the circuit and (b) the potential difference between the two terminals of the battery in closed circuit.
View SolutionA battery supplies a current of 0.9 A through a `2 Omega` resistor and a current of 0.3 A through a `7 Omega` resistor. Calculate the emf and internal resistance of the battery.
View SolutionA battery of emf 2.0 volts and internal resistance `0.10(Omega)`is being charged with a current of 5.0A. What is the potential difference between the terminals of the battery?
View SolutionA battery of emf 12.0 V and internal resistance `0.5 Omega` is to be charged by a battery charger which supplies 110 V d.c. How much resistance must be connected in series with the battery to limit the charging current to 5.0 A ? What will be the p.d. across the terminals of the battery during charging ?
View Solution(a)A car has a fresh storage battery of emf `12 V` and internal resistance `5.0 xx 10^(-2) Omega`. If the starter motor draws a current of `90A`, what is the terminal voltage of the battery when the starter is on?
(b) After long use, the internal resistance of the storage battery increase to `500 Omega`. What maximum current can be drawn from the battery? Assume the emf of the battery to remain unchanged.
(c) If the discharged battery is charged by an external emf source, is the terminal voltage of the battery during charging greater or less than its emf `12 V`?
View SolutionSix lead-acid type of secondary cells each of emf `2.0` V and internal resistance `0.015Omega` are jouned in series to provide a supply to a resistance of `8.5Omega`. What are the current drawn from the supply and its terminal voltage ?
(b) A secondary cells after long use has an emf of `1-9` V and a large internal resistance of `380 Omega`. What maximum current can be drawn from the cell ? Could the cell drive the starting motor of a car ?
View SolutionThree cells of emf 2.0 v, 1.8 V and 1.5 V are connected in series. Their internal resistances are `0.05 Omega, 0.7 Omega " and " 1 Omega` respectively. If the battery is connected to an external resistor of `4 Omega` via a very resistance ammeter, what would be the reading in the ammeter ?
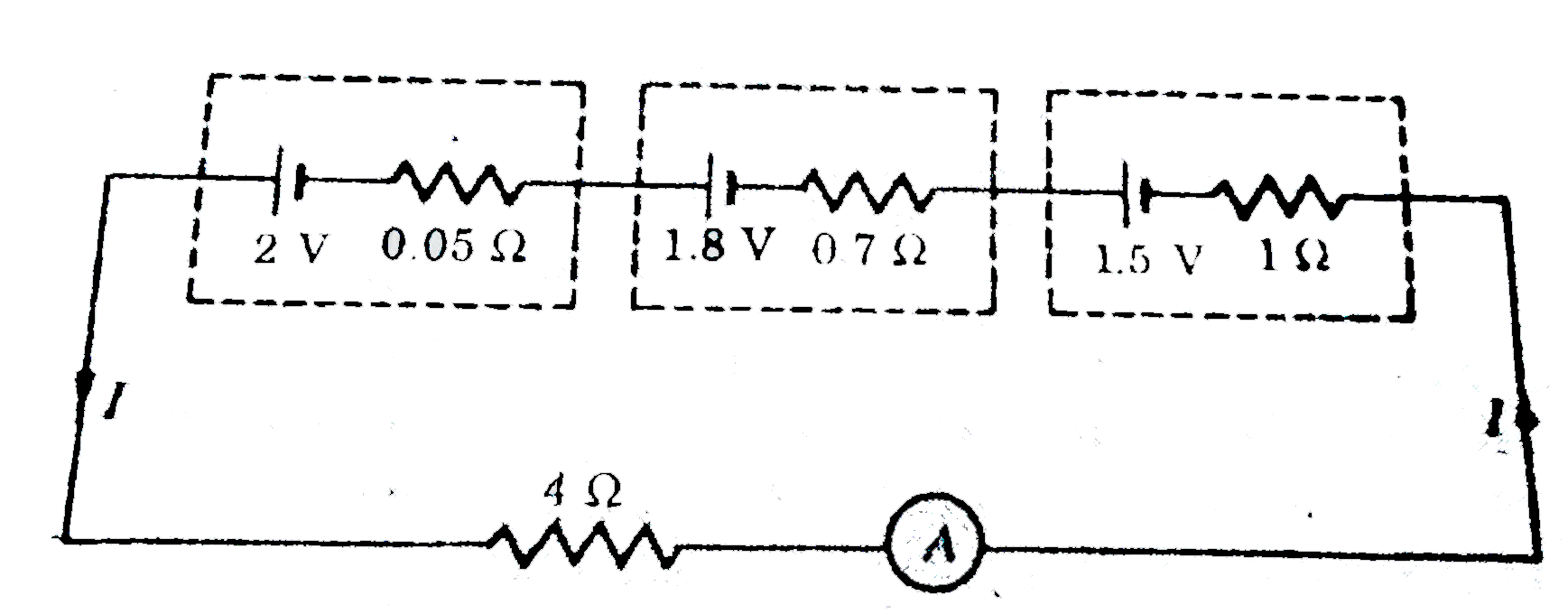
View SolutionA cell of emf `1.1 V` and internal resistance `0.5 Omega` is connected to a wire of resistance `0.5 Omega`. Another cell of the same emf is connected in series bur the current in the wire remain the same .Find the internal resistance of second cell
View SolutionTwo identical cells of emf 1.5 V each joined in paralllel provide supply to an external circuit consisting of two resistances of `17 Omega` each joined in parallel. A very high resistance voltmeter reads the terminal voltage of cells to be 1.4 V. Calculate the internal resistance of each cell.
View SolutionTwo cells `E_(1) " and " E_(2)` of emfs 4 V and 8 V having internal resistances `0.5 Omega " and " 1.0 Omega` respectively are connected in opposition to each other. This combination is connected in series with resistances of `4.5 Omega " and " 3.0 Omega`. Another resistance is connected in parallel across the `3 Omega` resistor.
(a) Draw the circuit diagram
(b) Calculate the total current flowing through the circuit.
View SolutionIn the circuit diagram given in Fig. 4.31, the cells `E_(1) " and " E_(2)` have emf's 4 V and 8 V and internal resistances `0.5 Omega " and " 10 Omega ` respectively. Calculate the current in each resistance .
View SolutionIn Fig. 4.32 `epsilon_(1) " and " epsilon_(2)` are respectively 2.0 V and 4.0 V the resistances `r_(1),r_(2)` and R are respectively `1.0 Omega, 2.0 Omega " and " 5.0 Omega`. Calculate the current in the circuit. Also calculate (i) potential difference between the points b and a, (ii) potential difference between a and c.

View SolutionA network of resistances is connected to a 16 V battery with internal resistance of `1 Omega`, as shown in Fig. 4.33.

(a) Compute epuivalent resistance of the network,
(b) obtain the current In in each resistor, and
(c ) obtain the voltage drops `V_(AB), V_(BC) " and " V_(CD)`.
View SolutionA galvanometer together with an unkonwn resistance in series is connected across two identical cells, each of emf 1.5 V. When the cells are connected inseries, the galvanometer records a current of 1 A and when the cells are connected in parallel, the current =0.6 A. What is the internal resistance of each cell ?
View SolutionA cell of emf 1.5 V and internal resistance `0.5 Omega` is connected to a (non-linear) conductor whose V-I graph is shown in Fig. 4.36 (a). Obtain graphically the current drawn from the cell and its terminal voltage.
View SolutionThirty six cells each of emf 1.5 V and internal resistance `0.5 Omega` are used to send current through an external resistor of resistance `2 Omega`. What is the best mode of grouping them and the current through the external resistor
View SolutionThree cells each of emf 1.5 V, after being connected in series with each other, are connected to the ends of a resistance. The current obtained is 1 A. When the cells are connected in parallel across the ends of the same resistance, the current is found to be 0.36 A. Find the external resistance and the internal resistance of each cell.
View SolutionThe ends of a resistance are connected to 19 cells in series, each of resistance `0.1 Omega`. The current is found to be 2 A. The number of cells is reduced to 15 and an extra resistance of `9.5 Omega` is connected in series to the given resistance. The current becomes one-half. Find the given resistance and emf of each cell.
View Solution
Example questions and complete solutions for chapter CURRENT ELECTRICITY of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 12