Complete Solutions to Based on Intensity Distribution in interference pattern of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| SL ARORA | Based on Intensity Distribution in interference pattern |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
The two slits in Young's experiment have widths in a rations `100 :1` . Find the ratio of light intensity at the maxima and minima in the interference pattern .
View SolutionThe ratio of intensity at maxima and minima is `25:16` . What will be the ratio of the width of the two slits in Young's double slit experiment ?
View SolutionTwo coherent sources whose intensity ratio `81:1` produce interference fringes . Calculate the ratio of intensity of maxima and minima in the fringe system .
View SolutionTwo slits in Young's interference experiment have widths in the ratio `1:16` . Deduce the ratio of intensity at maxima and minima .
View SolutionIn a Young's double slit experiment , the intensity of light at a point on the screen where the path difference is `lambda` is k units. Find the intensity at a point where the path difference is (a) `(lambda)/(4)` (b) `(lambda)/(3)` and (c) `(lambda)/(2)`
View SolutionTwo coherent monochromatic light beam of intensities I and 4I are supposed. What will be the maximum and minimum possible intensities.
View Solutionthe width of the one of the two sites in a Young's double slit experiment is double of the other slit. Assuming that the amplitude of the loight coming from a slit is propotional to the slit width, find the ratio of the maximum to the minimum intensity in the interference pattern.
View SolutionTwo light waves superposing at the midpoint of the screen are coming from coherent sources of light of phase difference `3 pi` radian. Their amplitudes are 1 cm. What will be the resultant amplitude at the given point.
View SolutionMonochromatic light of wavelength 600 nm is used in a Young's double slit experiment. One of the slits is covered by a transperent sheet of thickness `1.8xx10^(-5)`m made of a material refrective index 1.6. How many fringes will shift due to the introduction of the sheet ?
View SolutionFind the thickness of a plate which will produce a change in opticle path equal to half the wavelength `lambda` of the light passing through it normally. The refractive index of the plate is `mu`.
View SolutionIn Fresnel's Biprism experiment, on inserting a thin plate of glass in the path of one of the interfering beames, it is found that the central bright fringe shifts into the position perviously occupied by the 6th bright fringe. If ther wavelength of the light used is `6xx10^(-5)`cm and the refractive index of glass plate is 1.5 for the wavelength, calculate thethickness of the plate.
View SolutionA transparent paper (`mu`=1.45) of thickness 0.023 mm is pasted on one of the sdlits of a Young's double slit experiment which uses monochromatic light of wavelength 620 nm. How many fringes will cross the centre if the paper is removed ?
View SolutionA glass plate of `1.2xx10^(-6)`m thickness is placed in the path of one of the interfering beams in a biprism arrangement using monochromatic light of wavelength 6000 Å. If the central bands shifts by a distance equal to the width of the bands, find the refractive index of glass
View SolutionA soap film of `5xx10^(-15)`cm thick is viewed at an angle of `35^(@)` to the normal. Find the wavelength of light in the visible spectrum which will be absent from reflected light `(mu=1.3)`. Given wavelength range of the visible spectrum is 3900 Å to 7800 Å.
View SolutionA thin film of thickness `4xx10^(-5)` cm and `mu`=1.5 is iluminated by white light incident normal to its surface. What wavelength in the visible range be intensified in the reflected beam ?
View SolutionIn a thin film between two points A and B, eight fringes are observed with light of wavelength 5461 Å. How many fringes will be observed between the same two points A and B if the wavelength of the light used is 6500 Å.
View SolutionWith a thin air film between two points, 6 fringes appear when light of wavelength 5890 Å is used. Calculate the difference in the thickness of the film between the two points.
View SolutionWhite light is incident normally on a plane parallel thin film of µ=1.5. Find the minimum thickness of the film for which light of `lamda`=4000 Å is absent from the reflected light
View SolutionWhite light is incident on a soap film at an angle of `sin^(-1(4)/(5))` and the reflected light on examination by the spectroscope shows dark bands. The consecutive dark bands corresponds to wavelength 6100 Å and 6000 Å. If the refractive index of the film is 4/3, calculate its thickness.
View SolutionA soap film of refractive index 4/3 and thickness `1.5xx10^(-4)`cm is illuminated by white light incident at angle `45^(@)`. The reflected light is examined by a spectroscope in which a dark band corresponding to the wavelength `5xx10^(-5)` cm is found. Find the order of the interference band
View SolutionA parallel beam of sodium light of wavelength 5896 Å is incident at angle `30^(@)`. Find the minimum thickness of the glass plate for which the transmitted beam appears to be dark.
View SolutionA soap bubble of µ=4/3 is illuminated by white light incident at an angle of `30^(@)`. The transmittedlight is examined by a spectroscope and bright band is found for a wavelength of 6000 Å. Find the thickness of the film.
View SolutionMicrowaves of frequency 24,000 MHz are incident normally on a rectengular on a rectangular slit of width 5 cm. Calculate the angular spread of the central maximum of the diffraction pattern of the slit.
View SolutionA slit 4.0 cm wide is irradiated with microwaves od wavelengths 2.0 cm. Find the angular spread of the central maximum, assuming incidence normal to the plane of the slit.
View SolutionA screen is placed 2 m away from a single narrow slit which is illuminated by the light of wavelength `6xx10^(-7)`m. If the first minimum lies 4 mm on either side of the central maximum, find the width of the slit.
View SolutionThe light of wavelength 600 nm is incident normally on a slit of width 3 mm. Calculate the linear width of central maximum on a screen kept m awy from the slit.
View SolutionA slit of width 'd' is illuminuted by red light of wavelength 6500 Å. For what value of 'd' will (i) the fiirst minimum fall at an angle of defraction of `30^(@)` and (ii) the first maximum fall at an angle of diffraction of `30^(@)`.
View Solutiona 0.02 m wide slit is illumijnated at normal incidence by light of wavelength 6000 Å (i) Find the width of the central maximum band on the screen placed 1 m awayb from the slit. (ii) What should br the fringe width if the appratus Is impressed in water whose refractive index is 4/3?
View SolutionA parallel beam of light of wave length `6xx10^(-7)`m falls normally on a straight slit of width 0.2 mm. Find the totalk angular width of the central diffraction maximum and also its linear width as observed on a screen placed 2 m away.
View SolutionA Franhoffer diffraction pattern due to a single slit of width 0.2 mm is being obtained on a screen placed at a distance of 2 m from the slit. The first minima lie at 5mm in either side of the centre maximum on the screen. Find the wavelength of the light used .
View SolutionA parralel beam of monochromatic light of wavelength 5000 Å is incident normally in a narrow slit of width 0.25 mm. The diffraction pattern is observed on a screen placed at a focal lens of a convex lens placed closed to the slit between slit and screen. Find the angular seperatiion between the first secondary maxima on either side of the central maximum.
View SolutionA beam of light of wavelength 590 nm is focused by a convex lens of diameter 10 cm at a distance of 20 cm from it. Find the diameter of the disc image formed.
View SolutionA laser beam has a wavelength of `6xx10^(-7)`m and aperture of `6xx10^(-2)`m. The beam is sent towards the moon which is at a distance of `4xx10^(8)`m from the earth. Calculate (i) angular spread of the beam and (ii) the arel spread when it reaches the moon.
View SolutionA laser beam has a power of 100 mW. It has an aperture of `5xx10^(-3)`m and emits a wavelength 6943 Å. The beam is focused with a lens of focal length 0.1 m. Calculate the areal spread and intensity of the image.
View SolutionThe width of an aperture is 4 mm and wavelength is 5000 Å. Calculate the distance upto which ray optics is valid.
View SolutionFor what distance is ray optics a good approximation when the aperature is 3 mm wide and the wavelength 500 nm.
View SolutionTwo tower are built on the hill 50 Km apart and then joining them passes 30 m above a hill halfway in between. What is the longest wavelength of radiowaves which can be sent between the toers without serious diffraction effects ?
View SolutionA diffraction has 5000 lines per cm. What is its grating element ?
View SolutionA parallel beam of monochromatic light is incident normally on a plane transmision grating having 5000 lines per cm and the second order spectral ,ine is found to be diffracted through `30^(@)`. Calculate the wavelength of light used.
View SolutionSodium light of wavelength 5890 Å is incident normally on a diffraction grating of 5000 rulings per cm. Find the angle of diffraction for the second order.
View SolutionThe angle of diffraction of the second order maximum of wavelength `5xx10^(-5)` cm is `30^(@)` in the case of a plane transmission grating. How many lines are there in 1 cm of the grating surface.
View SolutionHow many orders will be visible if the wavelength of the incident radiation is 5000 Å and the number of lines on the grating is 101319 per metre.
View SolutionIn a grating experiment red line of wavelength `7000xx10^(-10)`m in the third order coincides with violet line in the fifth order. What is the wavelength of the voilet line?
View SolutionA parallel beam of white light is incident normally on a diffraction grating having 6000 lines per cm. Calculate the angular separation of red and viotet lights to be `7 xx 10^(-7)` m and `4 xx 10^(-4)` m respectively.
View SolutionA plane tansmission grating 6000 lines per cm is used to obtain a spectrum of light from a sodium lamp in the second order.Find the angular separation between two sodium line s whose wavelengths are `5890 Å` and `5896 Å` ,respectively.
View SolutionIf yellow light of `5890 Å` is incident on a grating that has 850 lines per mm. what will be the angle between both the first order images?
View SolutionLight froma galaxy, having wavelength of 6000 `Å` , if found to be shifted towards red by 50 `Å` . Calculate the velocity of recession fo the galaxy.
View SolutionThe spectral line of `lambda=5000 Å` in the light coming from a distant star is observed at 5200 `Å` . Determine the recession velocity of the star.
View SolutionThe spectral line in the spectrum of light from a star is found to be shifted by 0.032% from its normal position towards the red end of the spectrum . Compute the velocity of the star.
View SolutionAn astronaut approaching the moon sends a radio signal of frequency `5 xx 10^(3)` MHz towards moon to find the speed of his rocket . The frequency of waves reflected back from the moon to find the speed of his rocket . The frequency .Calculate the velocity of the rocket relative to the moon.
View SolutionA star is moving away from an observer with a speed of `500 kms^(-1)` .Calculate the Doppler shift if the wavelength of light emitted by the star is 6000`Å`.
View SolutionA star is moving towards the earth with a speed of `9.0 xx10^(6) ms^(-1)` . If the wavelength of a particular spectral line emitted by it si 6000 `Å` , then find the apparent wavelength.
View SolutionUnplarised light falls on two polarising sheets placed one on the top of the other what must be the angle between the characteristic directions of the sheets if the intensity of the transmitted light is (a) one-third of the maximum intensity of the transmitted beam (b) one third of the intensity of the incident beam.
View SolutionTwo nicols are so oriented that the maximum amount of light is transmitted .To what fraction of its maximum value is the intensity of the transimitted light reduced when the analyser is rotated through (i)` 45^(@) (ii)90^(@) (iii)180^(@)`
View SolutionWhen a polariser and analyser have their axes inclined to one another at `30^(@)` , the amount of light transmitted is 5 SI units. What is the maximum intensity of light transmitted and at what angle between the two?
View SolutionThe intensity of a light- beam is 10 `Wm^(-2)` and it is plane-polarised in vertical direction. It passes through a polaroid whose transmission axis is inclined at angle of `30^(@)` with the vertical. The transmitteed light- beam passes through a second polaroid whose transmission-axis is inclined at an angle of `90^(@)` with the vertical. (i) What will be the intesity of light emerging from the second polaroid? (ii) If the first polaroid is removed, then?
View SolutionFour polaroids are so placed that the transmission-axis of each is inclined at an angle of `30^(@)` from the axis of the previous polaroid in the same direction. If unpolarised light-beam of intensity `I_(0)` falls on the first, polaroid, then what will be the intensity of the light emerging from the last polaroid?
View SolutionFind the Brewstar angle for air-water surface for yellow light. Refractive index of water for yellow light =1.33
View SolutionA ray of light strikes a glass plate at an angle of incidence `57 ^(@)` . If the reflected and refracted rays are perpendicular to each other, what is the refractive index of glass.
View SolutionIn Fig. 16.13, at what angle `theta` above the horizon should the sun be situated so that its light reflected from the surface of still water of the pond be totally polarised? Given: refractive index of water `mu=1.327 " and " tan 53^(@)=1.327`.
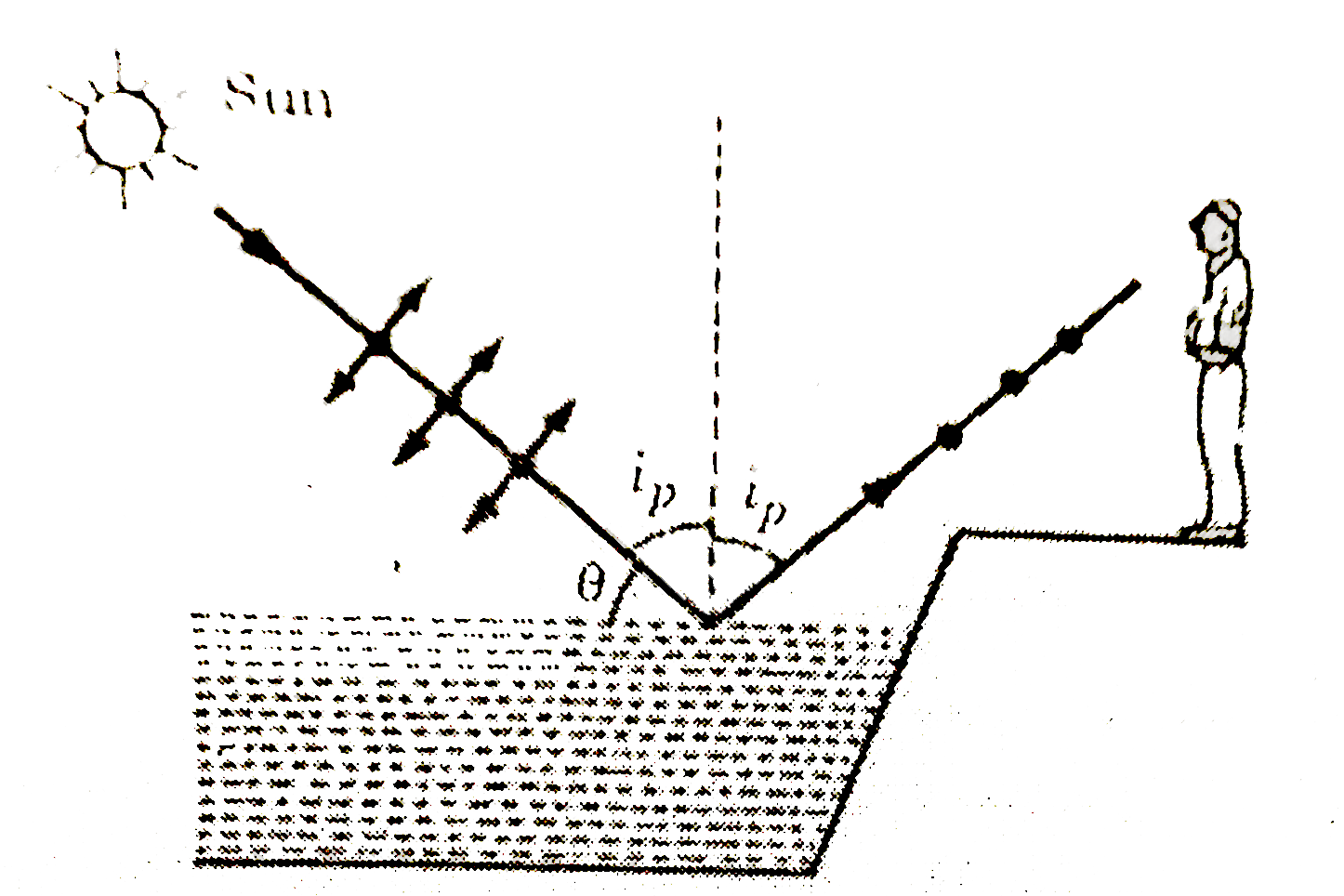
View SolutionWhen sunlight is incident on water at an angle of `53^(@)`, the reflected light is found to be completely plane-polarised. Determine (i) angle of refraction of light and (ii) refractive index of water.
View SolutionThe polarising angle for a medium is `60^(@)`. Determine (i) the refraction index of the medium and (ii) the refracting angle.
View SolutionA ray of light is incident on a transparent plate of a material of refractive index `sqrt(3)` at the polarising angle. Find the angle of refraction.
View SolutionA ray of light is incident on a glass plate of refractive index 1.54. If the reflected ray is completely plane polarised, find (i) angle of incidence (ii) angle of refraction and (iii) crictical angle. Given `tan 57^(@)=1.54` and `sin 40.5^(@)`=0.6493.
View SolutionYellow light is incident on a smooth surface of a block of dense flint glass for which the refractive index is 1.6640. Find the polarising angle and the angle of refraction.
View SolutionA beam of light travelling in water falls on a glass plate immersed in water. When the incident angle is `51^(@)`, the reflected beam of light is found to be completely plane polarised. Determine the refractive index of glass. Given refractive idex of water =4/3.
View SolutionThe critical angle of a for a medium is `45^(@)`. What is its polarising angle.
View SolutionThe critical angle for a certain wavelength of light is glass is `40^(@)`. Calculate the polarising angle and the angle of refraction in glass corresponding to it.
View SolutionA clear crystal has a critical angle of `24.4^(@)` for green light. What is the polaring angle of incidence ?
View SolutionCalculate the thickness of a quarter-wave plate of quartx for sodium light. Given `mu_(0)=1.54425 and mu_(E)=1.55336`.
View SolutionPlane polarised light is inciden on a piece of quartz cut parallel to the axis Find the least thickness for which the O and E-rays suffer a phase change of `pi//2`. Given `mu=1.5442 and mu_(E)=1.5533 and lambda=5xx10^(-7)m`.
View SolutionPlane polarised light is inciden on a piece of quartz cut parallel to the axis Find the least thickness for which the O and E-rays suffer a phase change of `pi//2`. Given `mu=1.5442 and mu_(E)=1.5533 and lambda=5xx10^(-7)m`.
View SolutionA quartz plate is a half wve plate for light whose wave length. Is `lambda`. Assuming that the variations is the indices of refraction with wavelength can be neglected, how would this behave with repsect to light of wavelengt `lamda=2lamda`.
View SolutionCalculate the specific rotation of sugar solution from the following data:
length of the polaimeter tueb=0.21
concentration of sugar solution =`80kgm^(-3)`
angle of rotation =`10^(@)`
View SolutionCalculate the amount of sugar dissolved in `10^(-3)m^(3)` of water so as to produce ratation of plane of polarisation of `12^(@)`. Given the specific rotation of sugar solution is`0.01 rad m^(-1) kg^(-1) m^(3)` and length of polarimeter tube is 0.21m
View SolutionA 22cm long tube containing 88cc of sugar produces an optical rotation of `9.9^(@)` when placed in a polarimeter. If the amount of sugar in the solution is 6g, calculation the specific rotation.
View SolutionA 0.12kg of impure sugar is dissolved in water and solution is mad eupto `8xx10^(-4)m^(3)`. A length of 20cm of this solution causes a rotation of `15^(@)`. If the specific rotation of sugar is `60xx10^(@) deg//decimetre kg `m^(-3)`, what is the purity of sugar?
View SolutionA solution of camphor in alcohol in a tube 20cm long is found to effect a rotation of the plane of viberation of light passing is of `33^(@)`. What must be the indentify of camphor in `g//cm^(2)` in solution? The specific rotation of camphor is `+54^(@)`.
View SolutionA plate of crystal quartz is cut with its faces perpendicular to the optic axis. It is found that this plane exactly annuls the rotation of the plane of polarisation of sodium light produced by a 30 cm length of a `18^(@)` solution of lactose. Calculate the thickness of the quartz plate. Given 's' for lactose =`5253^(@), 1 mm of quartx rotats the plane of polarisation of sodium light by `21.71^(@)`.
View SolutionA polarimeter tube of length 0.21m contains sugar solution of specific rotation 0.01 rad `m^(-1)kg^(-1)m^(3)` concentration. If the produced is `36^(@)`, calculate the concentration of the solution. The solution is the tube is poured into a clean beaker and equal amount of water id added to it. The tube is then filled with the diluted solution. Calculate the angle of rotation produced.
View Solution
Based on Intensity Distribution in interference pattern questions and complete solutions for chapter WAVE OPTICS of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 12