Complete Solutions to Problems from competitive examination of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| SL ARORA | Problems from competitive examination |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
Two sources of intensity I and 4 are used in an interference experiment. Find the intensity at point where the waves from two sources superimpose with a phase difference (i) zero (ii) `pi//2` and (iii) `pi`.
View SolutionA narrow monochromatic beam of light of intensity I is incident on a glass plate. Another identical glass plate is kept close to the first one and parallel to it. Each plate reflects 25% of the incident light and transmits the remaining. Calculate the ratio of minimum and maximum intensity in the interference pattern fromed by two beams obtained after reflection from each plate.
View SolutionIn a ratio slit experiment with monochromatic light, fringses are obtained on a screen placed at some distance from the slits. If the screen is moved `5xx10^(-2)m` towards the slits, the change in fringe width is `3xx10^(-5)`. If the distance. Between the slits is `10^(-3)m`, calculate the wavelength of the light used.
View SolutionIn a Yong's double-slit experiment, the separration between slits is `2xx10^(-3)`m whereas the distance of screen from the slits is 2.5m. A light of wavelength in the range of 2000-8000Å is allowed to fall on the slits. Find the wavelength length in the visisble region that will be present on the screen at `10^(-3)`m, from the central maximum. Also find the wavelength that will that will be present at that point of screen in the infrarred as awil as in the ultraviolet region.
View SolutionIn Young's double-slit experiment the angular width of a fringe formed on a distant screen is `1^(@)`. The wavelength of light used is `6000 Å`. What is the spacing between the slits?
View SolutionA double slit arrangement produces interference fringes for sodium light `(lambda = 5890 Å)` that are `0.40^(@)` apart. What is the angular fringe separation if the entire arrangement is immersed in water?
View SolutionThe interference fringes for sodium light `(lambda = 5890 Å)` in a double slit experiment have an angular width of `0.2^(@)`. For what wavelength will width be `10%` greater.
View SolutionA two slit Young's interference is done with monochromatic light of wavelength 6000Å. The slites ar e2mm apart and fringes are observed on a screen placed 10cm away fromm the slits and it is found that the interference pattern shifts by 5mm, when a transparent plate of thickness 0.5mm is introduced in the path of one of slits. What is the refractive index of the transparent plate?
View SolutionA double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit and the screen 1 mm. The slits are illuminated by a parallel beam of light whose wavelength in air is `6300 Å`
a. calculate the fringe width.
b. One of the slits of the apparatus is covered by a thin glass sheet of refractive index 1.53. Find the smallest thickness of the sheet to bring athe adjacent minima on the axis.
View SolutionIn a Young's experimenttje upper slit is covered by a thin glass plate of refractive index. 1.4 while the lower slit is covered with another glass plate, having the same thickness as the first one but having refravtive index 1.7. Interference pattern is observed using light of wavelength 5400Å. It is found that the point P on the sreen where the central where the central maximum (n=0) fell before the glass plates were inserted now has 3/4 the original intensity. It is further observed that what used to be the fifth maximum earlie, lies shown the point P while the sixth minimum lies above P. Calculate the thickness of glass plate. (Absorption of light by a glass may be neglected).
View SolutionIn a Young's interference experimental arrangement, the incident yellow light is composed of twpo wavelength 5890Å. The distance between of the two slits is `10^(-3)m` and screen is placed 1m away. Upto what order can frings be seen on the screen and how far from the centre of the screen does this occur?
View SolutionIn young,s double slit experience monochromatic light, the frings pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 microns is introduced in the path of one of the interfering waves. The mica sheet is then sheet is then removed and the distance between the slits and the screen is doubled. It is found that now the distance between succesive maximum (or minimum) is the same as the observed fringe-shift upon the introduction o fthe mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
View SolutionMonochromatic light of `lamba=5000Å` is incident on two slits separately by a distance of `5xx10^(-4)m`. The interference patteren is seen on a screen placed at a distance of 1m form the slits. A thing glass plate of thicknes `1.5xx10^(-6)m` and refractive index `mu=1.5` is placed between one of the slits and the screen. Find the intensity at the centre of the screen if the density there is `I_(0)` in the absence of the plate. Also find the lateral shift of the central maximum. '
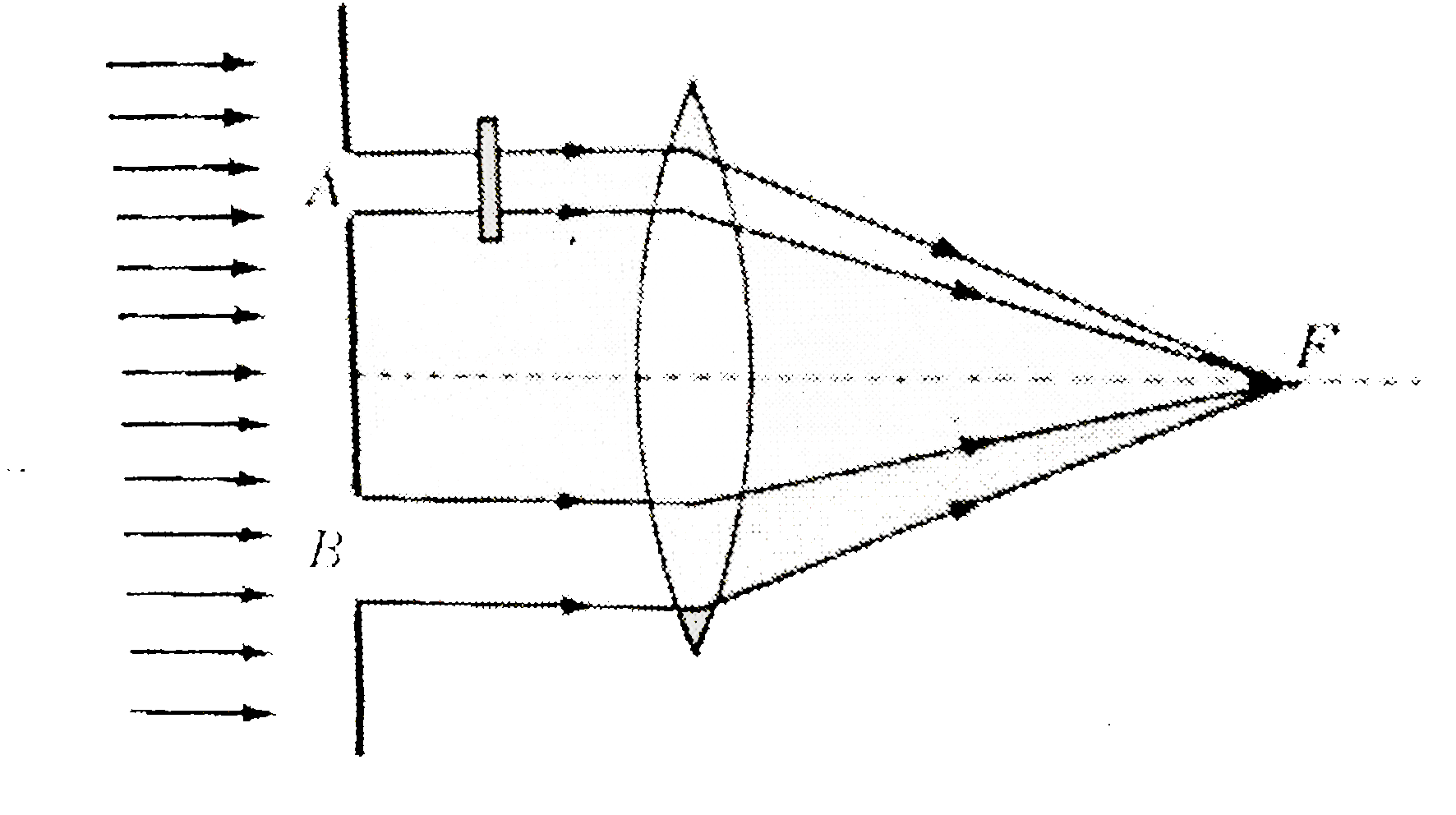
View SolutionIn a modified Young's double slit experiment a monochromatic uniform and parallel beam of light of wave length 6000Å and intensity `(10/pi)Wm^(-2)` is incident normally on two circular apertures A and B of radii 20009Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture. A. Calculate the power (in watt) received at the focal spot F of the lens. The lens is symmertrically placed with respect to the apertures. Assume that 10% of the power received by each aperture goes in the originally direction and is brought to the focal spot.
View SolutionIn figure S is a monochromatic point source emitting light of wavelength `lambda=500 nm`. A thin lens of circular shape and focal length `0.10 m` is cut into two identical halves `L_(1)` and `L_(2)` by a plane passing through a doameter. The two halves are placed symmetrically about the central axis `SO` with a gap of `0.5 mm`. The distance along the axis from `A` to `L_(1)` and `L_(2)` is `0.15 m`, while that from `L_(1)` and `L_(2)` to `O` is `1.30 m`. The screen at `O` is normal to `SO`.
(a) If the `3^(rd)` intensity maximum occurs at point `P` on screen, find distance `OP`.
(b) If the gap between `L_(1)` and `L_(2)` is reduced from its original value of `0.5 mm`, will the distance `OP` increases, devreases or remain the same?

View SolutionWhite light is used to illuminate the two slits in a Young's double slit experiment. The separation between the slits is b and theh screen is at a distance `d (gt gtb)` from the slits At a point on the screen directly in front of one of the slits, certain wavelengths are missing some of these missing wavelengths are
View SolutionAngular width of central maximum in the Fraunhoffer diffraction pattern of a slit is measured. The slit is illuminated by light of wavelength `6000Å`. When the slit is illuminated by light of another wavelength, the angular width decreases by `30%`. Calculate the wavelength of this light. The same decrease in the angular width of central maximum is obtained when the original apparatus is immersed in a liquid. Find the refractive index of the liquid.
View SolutionThe limits of the visible spectrum are 4000Å to 7000Å. Show that the violet of the thrid order visible spectrum overlaps the red of the second order spectrum produced by a plane diffraction grating having 15,000 lines per inch, when visible light is incident normally on the granting.
View SolutionThe wavelength of light coming from a distant galaxy is found to be `0.5%` more than that coming from a source on earth. Calculate the velocity of galaxy.
View SolutionAn astronaut is approaching the moon. He sends a ratio signal of frequency `5 xx 10^(9) Hz` and find that the frequency shift in echo received is `10^(3) Hz`. Find his speed of approach.
View SolutionTwo polaroids are placed at `90^(@)` to eachother. What happens when `(N - 1)` more polaroids are inserted between them ? Their axes are equally spaced. How does the transmitted intensity behave for large `N` ?
View SolutionUnpolarized light of intensity 32 `Wm^(-3)` passes through three polarizers such that the transmission axis of the last polarizer is crossed with the first. If the intensity of the emerging light is `3 Wm^(-2)`, what is the angle between the transmission axces of the first two polarizers ? At what angle will the transmitted intensity be maximum ?
View SolutionA beam of plane polarised falls normally on a polariser (cross section area `3xx10^(-4),^(2))` Find the energy of light pssing through the polariser per revolution and the intensisty of the emergent beam if the flux of energy of the incident ray is `10^(-3)W`.
View Solution
Problems from competitive examination questions and complete solutions for chapter WAVE OPTICS of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 12