Complete Solutions to Example of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| SL ARORA | Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The velocity of light in vacuum is `3xx10^(8)ms^(-1)`. What is the velcoity of light in glass if the index of refraction of glass if `1.5`?
View SolutionMonochromatic light of wvalength `589 nm` is incident from air on a water surface. What are the wavelength, frequency and speed of (a) reflected and (b) refracted light ? `mu` of water is 1.33`.
View SolutionThe wavelength of light coming from a sodium source is 589 nm. What will be its wavelength in water? Refractive index of water 1.33.`
View SolutionThe refractive index of diamond is `2.47` and that of glass is `1.51`. How much faster does light travel in glass than in diamond ?
View SolutionCalculate the time which light will take to travel normally through a glass plate of thickness `1 mm`. Refractive index of glass is `1.5`.
View SolutionWhite light is a mixture of light of wavelengths between 400 nm and 700 nm. If this light goes through water `(mu = `1.33)` what are the limits of the wavelength there ?
View SolutionThe optical path of a monochromatic light is the same if it goes through 2.00 cm of glass or 2.25 cm of water. If the refractive index of water is 1.33, what is the refractive index of glass?
View SolutionFor the same angle of incidence, the angles of refraction in media `P, Q and R` are `35^(@) ,25^(@), 15^(@)` resp. In which medium will the velocity of light be minimum ?
View SolutionIf `epsi_(0)` and `mu_(0)` are respectively, the electric permittivity and the magnetic permeability of free space, `epsi` and `mu` the corresponding quantities in a medium, the refractive index of the medium is
View SolutionA glass slab of thickness `4 cm` contains the same number of waves as `5 cm` of water, when both are traversed by the same monochromatic light. If the refractive index of water is `4//3,` then refractive index of glass is
View SolutionRefractive index of air is `1.0003.` The correct thickness of air column which will have one more wavelength of yellow light `(6000 Å)` than in the same thickness in vacuum is
View SolutionTwo slits are made one millimeter apart and the screen is placed one metre away. When blue-green light of wavelength 500 nm is used, the fringe separation is
View SolutionIn Young's double slit experiment the slits are separated by 0.24 mm. The screen is 2 m away from the slits . The fringe width is 0.3 cm. Calculate the wavelength of the light used in the experiment.
View SolutionIn Young's double slit experiment, while using a source of light of wavelength 4500 `Å` , the fringe width obtained is 0.4 cm. If the distance between the slits and the screen is reduced to half , calculate the new fringe width.
View SolutionIn Young's double slit experiment , the light has a frequency of `6 xx 10^(14) Hz` and the distance between the centres of adjacent fringes is `0.75 mm`. If the screen is `1.5m` away, what is the distance between the slits ?
View SolutionIn Young's double slit experiment the fringe width obtained is 0.6cm , when light of wavelength 4800 `Å` is used. If the disatance between the screen and the slit is reduced to half, what should be the wavelength of light used to obtain fringes 0.0045 m wide ?
View SolutionIn Young's double slip experiment ,the width of fringes obtained from a source of light of wavelength 5000 `Å` is 3.6mm Calculate the frings width if the apparatus is immersed in a liquid of refractive index 1.2.
View SolutionThe two slits in Young's double slit experiment are separated by a distance of 0.03 mm. An interference pattern is produced on a screen 1.5 m away. The 4th bright fringe is at a distance of 1 cm from the central maximum. Calculate the wavelength of light used.
View SolutionTwo slits `0,125 mm` apart are illuminated by light of wavelength `4500 Å`. The screen is `1m` away, from the plane of the slits. Find the separation between the 2nd bright fringe on both sides of the central maximum.
View SolutionIn Young's double slit experiment, the slits are `0.2 mm` apart and the screen is `1.5 m` away. It is observed that the distance between the central bright fringe and fourth dark fringe is `1.8 cm`. Calculate wavelength of light used.
View SolutionA double slit is illuminated by light of wave length 6000 Å. The slit are 0.1 cm apart and the screen is placed one metre away. Calculate.
(i). The angular position of the `10^(th)` maximum in radian and
(ii). Separation of the two adjacent minimal.
View SolutionIn Young's double slit experiment the slits are 0.5 mm apart and interference is observed on a screen placed at a distance of 100 cm from the slits. It is found that the `9^(th)` bright fringe is at a distance of 8.835 mm from the second dark fringe from the centre of the fringe pattern. Find the wavelength of light used.
View SolutionIn a Young's double experiment , the slits are 1.5 mm apart. When the slits are illuminated by a nonochromatic light source and the screen is kept 1 m apart from the slits ,width of 10 fringes is measured as 3.93 mm . Calculated the wavelength of light used. What will be the width of 10 fringes when the distance between the slits and the screen is increased by 0.5 m . The source of light used remains the same.
View SolutionTwo sources `S_(1)` and `S_(2)` emiting light of wavelenght 600 nm placed a distance `1.0 xx 10^(-2)` cm apart.
A detector can be moved on line `S_(1) P` which is perpendicular to `S_(1) S_(2)`
(a) What would be the minimum and maximum path difference at the detector as it moves along line `S_(1) P` ?
(b) Locate the psoition of the farthest minima detected
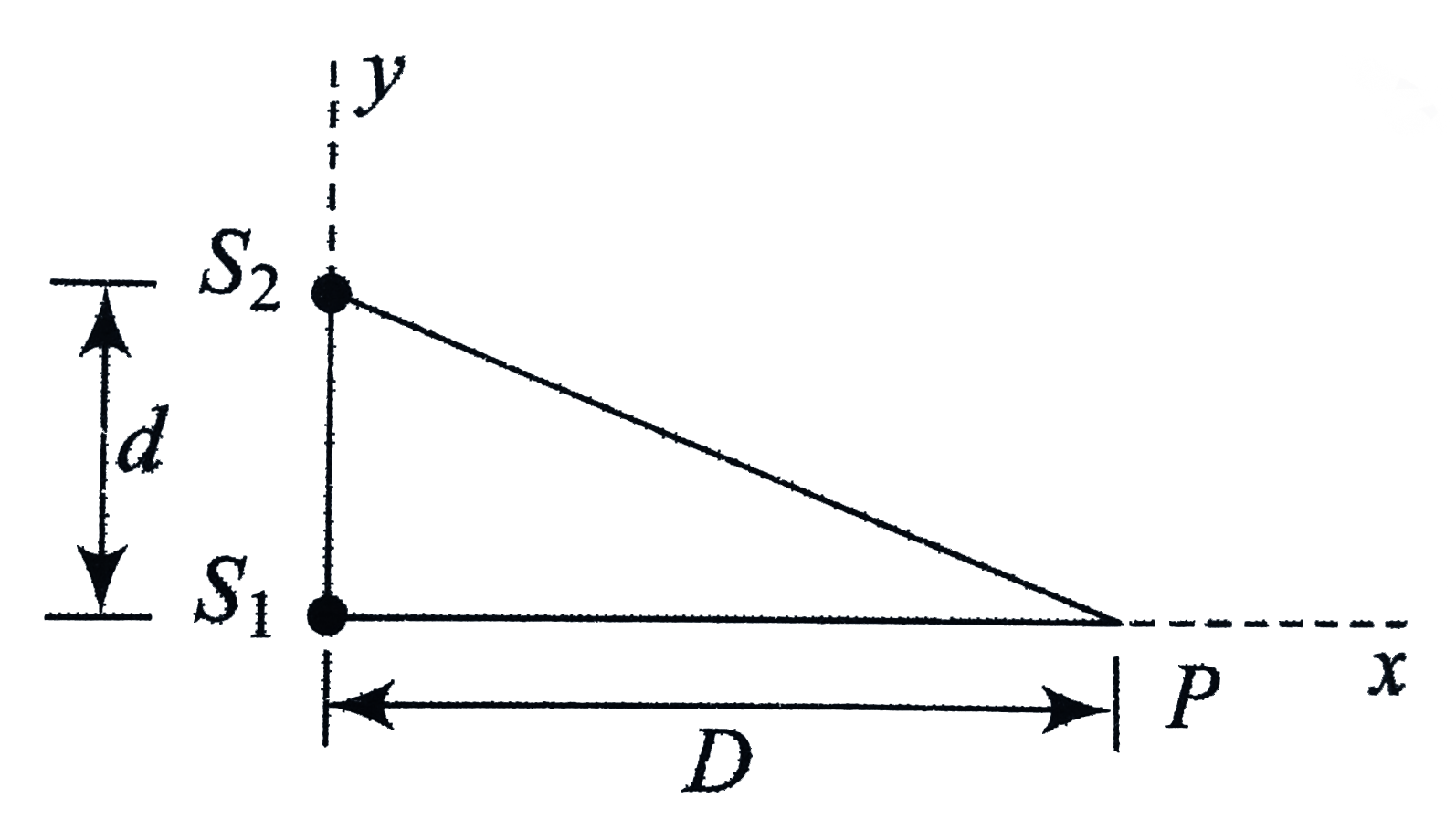 .
.
View SolutionIn Lloyd's single mirror interference experiment, the source slit is at a distance of 2 mm from the plane mirror . The screen is kept at a distance of 1.5m from the source . If light of wavelength 5890 `Å` is used, calculate the fringe width.
View SolutionIn Lloyd's interference experiment, 10 fringes occupy a space of 1.5 mm. The distance between the source and the screen is 1.25 m. If light of wavelength 6000 `Å` is used, find the distance of the source from the plane minor.
View SolutionIn Lloyd's experiment , the slit and its image have a separation of 4.32 mm and the obsevations made at a plane 2.0 m away fringes of separation 0.26 mm. Find the wavelength of light used.
View SolutionIn Lloyd's interference experiment, the path difference between direct and reflected beams of light for the 10th bright fringe was observed to be 0.63 mm. Find the wavelength of light used.
View SolutionIn a Fresnel's biprism experiment, sodium light of wavelength `5832 Å` is used. Calculated the fringe width, given the distance between the screen and the biprism =120 cm and the distance the two sources=0.04 cm.
View SolutionIn a biprism experiment , the slit is illuminated with light of wavelength `4800 Å` . The distance the slit and birprism is 20cm and that between biprism and eyepiece is 80cm . If two virtual source are 0.3 cm apart, determine the distance between the 5th bright band on one side of the central bright band and the 5th dark bank on the other side.
View SolutionIn a biprism experiment, the distance between 4th an 13th bright fringes is measured when light of wavelength `6 xx 10^(-7)` m is used. On replaceing the source by another of different wavelength without disturbing the adjustment of the apparatus , it is found that the distance between 5th and 15th bright fringes is the same as measured before, what is the wavelength of light used?
View SolutionIn a biprism experiment , fringe width is measured as 0.4 mm . When the eyepiece is moved away from the biprism through 30 cm, the fringe width increase by 50% if the two virtual soruces are 0.6 mm apart, find the wavelength of light used.
View SolutionIn a biprism experiment , the distance between the coherent source is 0.5 mm and that between the slit and the eyepiece is 1.2 m, the slit is illuminated by red light of wavelength `6500 Å` . If the red light is repluced by a green light of movelength`6550 Å` , it is found that the nth red band coincides with (n+1)th green bright band. Calculate the distance of these from the central bright band.
View SolutionInterference fringers are produced by a Fresnel's biprism in the focal plane of reading microscope which is 100 cm from the slit. A lens interposed between the biprism and the microscope gives two images of the slit in two positions.If the images of the slits are 4.05 mm apart in one case, 2.90 mmin the other and the wavelength of light used is 5893 Å, find the distance between two consecutive bands.
View SolutionTwo slits in Young's double slit experiment have widths in the ratio 81:1. What is the the ratio of amplitudes of light waves coming from them ?
View SolutionWhat is the ratio of slit widths when amplitudes of light waves from them have ratio `1 : sqrt(2)` ?
View SolutionThe phase difference between two waves reaching a point is `pi//2`. What is the resultant amplitude, if the individual amplitudes are `3mm and 4mm` ?
View SolutionConsider interference between waves form two sources of intensities `I&4I`.Find intensities at point where the phase difference is `pi`
View SolutionIn Young's double slit experiment, if `I_(0)` is intensity of light from each sources, what is the intensity at a point on screen where two waves arrive having a phase diff. of `60^(@)` and `120^(@)`.
View SolutionFind the ratio of intensities at the two points `X and Y` on a screen in Young's double slit experiment, where waves from the two source `S_(1) and S_(2)` have path difference of zero, and `lambda//4` respectively.
View SolutionTwo coherent sources whose intensity ratio is 81:1 produce interference fringes. Calculate the ratio of intensity of maxima and minima in the fringe systen.
View SolutionThe ratio of intensity at maxima and minima in the interference pattern is 25:9. What will be the widths of the two slits in Young's interference experiment ?
View SolutionTwo coherent sources of light of intensity ratio `beta` interfere. Prove that the interference pattern,`(I_(max)-I_(min))/(I_(max)+I_(min))=(2sqrtbeta)/(1+beta)`.
View SolutionThe ratio of the intensity at the centre of a bright fringe to the intensity at a point one-quarter of the distance between two fringe from the centre is
View SolutionFringes are produced with monochromatic light of wave-length `5.45xx10^(-5)` cm. A thin glass plate of refractive index 1.5 is then placed normally in the path of one of the interference beams and the central bright band of the fringe system is found to move into the position previously occupied by the third bright band from the system. Find the thickness of the glass plate.
View SolutionWhen a thin sheet of a transparent material of thinkness `7.2xx10^(-4)`cm is introduced in the path one of the interfering beams, the central fringe shift to a position occupied by the sixth bright fringe. If `lambda=6xx10^(-5)` cm, find the refractive index of the sheet.
View SolutionInterference fringes were produced by Young's double slit method, the wavelength of light used being 6000Å. The separation between the two slits is 2 mm.The distance between the slits and screen is 10 cm. When a transparent plate of thickness 0.5 mm is placed over one of the slits. the fringe pattern is displaced by 5 min. Find the refractive index of the material of the plate.
View SolutionA soap film is illuminated by while light incient at an angle of `30^(@)`. The reflected light is examined by a spectroscope in which a dark band corresponding to wavelength 6000Å is found . Calculate the minimum thickness of the film. Given refractive index of film`=(4)/(3)`
View SolutionWhite light reflected at perpendicular incidence from a soap film has, in the visible specturm, an interference amximum at 6000Å and a minimum at 4500Å with no minimum in between. If `mu=4//3` for film, what is the film thickness ?
View SolutionA soap film of `mu=(4)/(3)` is illuminated by white light incident at an angle of `45^(@)`. The transmitted light is examined by spectrospe and bright fringe is found to be for wavelength of 6000Å. Find the minimum thickness of the film.
View SolutionWhite light is incident on a soap film of `mu=4//3` at an angle of `30^(@)`. On examining the transmitted light with a spectrometer a dark band of wavelength `5.5xx10^(-7)` m is found. Find the minimum thickness of the film.
View SolutionA slit 4.0 cm wide is irradiated with microwaves of 2.0 cm. Find the angular spread of central maximum assuming incidence normal to the plane of the slit.
View SolutionA slit of width is illuminated by white light. For red light `(lambda=6500Å)`, the first minima is obtained at `theta=30^@`. Then the value of will be
View SolutionA screen is placed `2m` away from the single narrow slit. Calculate the slit width if the first minimum lies `5 mm` on either side of the central maximum. Incident plane waves have a wavelength of `5000 Å`.
View SolutionLight of wavelength 5500 Å falls on a slit on a slit of width 0.13 cm at normal incidence. Calculate the width of the central maximum on a screen kept 2.5 m away from slit.
View SolutionDetermine the angular spread between central maximum and first order maximum of the diffraction pattern due to a single slit of width `0.25 mm`, when light of wavelength `5890 Å` is incident on it normally ?
View SolutionRed light of wavelength `6500 Å` from a distant source falls on a slit `0.50 mm` wide. Calculate the distance between first two dark bands on each side of central bright band in the diffraction pattern observed on a screen placed `1.8 m` from the slit.
View SolutionParallel light of wavelength 5000 Å falls normally on a single slit. The central maximum spreads out to `30^(@)` on either side of the incident light.Find the width of the slit.For what width of the slit the central maximum would spread out to `90^(@)` from the direction of the incident light ?
View SolutionA slit of width 0.025 mis placed in front of a lens of focal length 50 cm. The slit is illuminated with light of wavelength 5900 Å. Calculate the distance between the centre and first dark band of diffraction pattern obtained on a screen placed at the focal plane of the lens.
View SolutionTwo spectral lines of sodium `D_(1)` and `D_(2)` have wavelengths of approximately 5890 Å and 5896 Å. A sodium lamp sends incident plane wave onto a slit of width 2 micrometre. A screen is located 2 m from the slit. Find the spacing between the first maxima of two sodium lines as measured on the screen.
View SolutionWhat should be the width of each slit to obtain `10` maxima of the double slit interference pattern within the central maximum of single slit diffraction pattern ? (NCERT Solved example)
View SolutionA laser operates at a frequency of `3xx10^(14)` Hz and has an aperture of `10^(-2)` m. What will be the angular spread ?
View SolutionA laser beam has a wavelength of `7 xx 10^(-7) m` and aperure `10^(-2)m`. The beam is sent to moon at a distance of `4 xx 10^(5) km` from earth. Find the angular spread and areal spread of the beam on reaching the moon.
View SolutionEstimate the distance for which ray optics is good approximation for an aperture of `4 mm` and wavelength `400 nm`.
View SolutionFor what distance is ray optics a good approximation when the aperture is `3 mm` wide and wavelength is `500 nm` ? (NCERT Solved Example)
View SolutionLight of wavelength `5000Å` is diffrated by an aperture of width `2mm`. For what distance by the diffracted beam does the spreading due to diffraction become greater than the width of the aperture ?
View SolutionLight of wavelength `600 nm` is incident on an aperture of size `2 mm`. Calculate the distance light can travel before its spread is more than the size of aperture.
View SolutionTwo towers on top of two hills are `40 km` apart. The line joining them passes `50 m` above a hill halfway between the towers. What is the longest wavelength of radio waves, which can be sent between the towers without appreciable diffraction effects ?
View SolutionA diffracting grating 1 cm wide has 1200 lines and is used in second order. What is the diffraction angle for light of wavelength 550 nm?
View SolutionA diffraction garating has 5,000 rulings per centimetre. What is the second order diffraction angle for violent light (`lamda` = 500 nm).
View SolutionA planetransmissiongratinghaveing 8000 lines per cm is hevingused at normal incidence. Find the longest wavelength which canbe obscraved in the first order.
View SolutionA diffraction grating having 600 lines per mm is illuminated normally by light of wovelength 600 `Å`What is the heghest order of diffraction image that can be seen ?
View SolutionA plane transmissio grating when illuminated with normal light produces a second order diffraction at `30^(@)` for wavelength `lamda`=500 `Å.` Calculate the number of lines per cm on the grating.
View SolutionAparallel beam of sodium lignt falls normally of a plane grating having 4240 lines per cm. A second order line is obseved at `30^(@)` to the normal. Find the wavelength. What is the highest order that can be observed with this grating? Will this line appear to be of the same colour in each order ?
View SolutionA. diffraction grating has 800 lines per mm and is illuminated normally by parallel monochromatic light of wavelengths 560 nm and 590 nm. Calculate the difference in the angular positions of the first order spectra of the two lights on th same suide of the normal.
View SolutionA diffraction grating used at normal incidence gives a line ` lamda_(1)=600Å` in a certain order supermposed on another line ` lamda_(2)=450Å` of the next higher order. If the angle of diffraction is `30^(@)` how many lines are there in 1 cm of the grating.
View SolutionThe `6563 Å H_(2)` line emitted by hydrogen in a star is found to be red shifted by `15 Å`. Estimate the speed with which the star is receding from earth.
View SolutionThe spectral line for a given element in the light received from a distant star is shifted towards longer wavelength side by `0.025%`. Calculate the velocity of star in the line of sight.
View SolutionEarth is moving towards a fixed star with a velocity of `30 kms^(-1)`. An observer on earth observes a shift of `0.58 Å` in wavelength of light coming from star. What is the actual wavelength of light emitted by star ?
View SolutionA plane electromagnetic wave of frequency `w_(0)` falls normally on the surface of a mirror approaching with a relativisitic velocity v. Then frequency of the reflected wave will be (given `beta=(v)/(c )`):
View SolutionThe red shift of radiation froma distance nebula consits of light known to hace a wavelength of 434 nm. In the laboratory, this wavelength appears to be 6562 `Å.` What is the speed of the nebulal in the line of sight relative to the earth ? Is it approching or receding ?
View SolutionGiven `v'=(1-v//c)vandv'=((1-v//c)v)/sqrt(1-v_(2)//c_(2))` For what value v/c, these question differ by 10%
View SolutionAn e.m. beam has an intensity of 20 `Ww^(-2)` and is linearly poorised in the vertical direction. Find the intensity of the transmitted beam by a polaroid when its plan of transmission makes an angle of `60^(@)` with the vertical.
View SolutionTwo polarising sheets are placed with their planes parallel, so that light intensity transmitted is max. Through what angle must either sheet be turned so that light intensity drops to half the maximum value ?
View SolutionTwo nicols are so oriented that the maximum amount of light is transmitted. To what fraction of its maximum value is the intensity of transmitted light reduced when the analyser is rotated through (i) `30^(@)` (ii) `60^(@)` ?
View SolutionTwo polaroids are placed at `90^(@)` to each other and the transmitted intensity is zero. What happens when one more polarid is placed between these two bisecting two bisecting the angle between them?
View SolutionAs polaroid examines two adjacent plane polarised beam A and B whose planes of polarisation are mutually perpendicular. In the first position of the analyser, beam B shows zero intensity. From this position a rotation `30^(@)` shows that thebeams have same intensity. The ratio of intensity of the two beam `I_(Z) & I_(B)`
View SolutionTwo 'crossed' polaroids A and B are placed in the path of a light-beam. In between these, a third polaroid is C is placed whose polarisation axis makes an angel `theta` with a polarisation axis of the polaroid A. If the intensity of light emerging from the poloaroid a is `I_(o)` then show that the intensity of light emerging from polaroid B will be `1/4I_(o) sin^(2)theta.`
View SolutionWhat is Brewster angle for air to glass transtion ? (`mu` of glass is `1.5`)
View SolutionYellow light is incident on the smooth surface of a block of dense flint glass for which the refractive index is 1.6640. Find he polarising angle. Also find the angle of refraction.
View SolutionA ray of light in incident on a glass plate at an angle of `60^@`. What is the refractive index of glass if the reflected and refracted rays are perpendicular to each other?
View SolutionAt what angle of incidence will the light reflected from water `(mu=1.3)` be completely polarised?
View SolutionShow that when a ray of light is incident on the surface of a transparent medilum at the polarising angle, the reflected and transmitted rays are perpendicular to each other.
View SolutionFor given medium, the polarising angle is `60^(@)`. What will be the critical angle for this medium ?
View SolutionThe velocity of light in air is `3xx10^(8)ms^(-1)` and that in water is `2.2xx10^(8)ms^(-1).` Find the polrising an gle of incidence.
View SolutionThe refractive index of water is 4/3 and that of glass 3/2. A beam of light travelling in wter enters glass. For what angle of incidence the refected light will be completely plane-polarised? (than `48^(@)22` = 1.125)
View SolutionCalculate the thickness of (i) a quarter wave plate (ii) a half-wave plate, given that `mu_(e)`=1.533 `mu_(o)`=1.544 `lamda=5000 Å.`
View SolutionA beam of linearly polarised is change into circularly palarised light by passing it through a slice of cryslal 0.003 cm thick. Calculate the difference n the refractive index of the two rays in the crystal assuming this to be minimum thickness that wil produce the effect and that the wavelength is `6xx10^(-5)` cm.
View SolutionCalculate the specific rotation if the plane of polarization is turned through `13.2^(@)` traversing a length of 20 cm of 10% sugar solution.
View SolutionA certain length of 50% solution produces an optical rotation of `20^(@).` How much length of 10% solution of the same substance will produce a rotation of `30^(@)`
View Solution
Example questions and complete solutions for chapter WAVE OPTICS of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 12