Complete Solutions to JEE Main And Advanced of chapter MOVING CHARGES AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOVING CHARGES AND MAGNETISM |
| SUNIL BATRA | JEE Main And Advanced |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
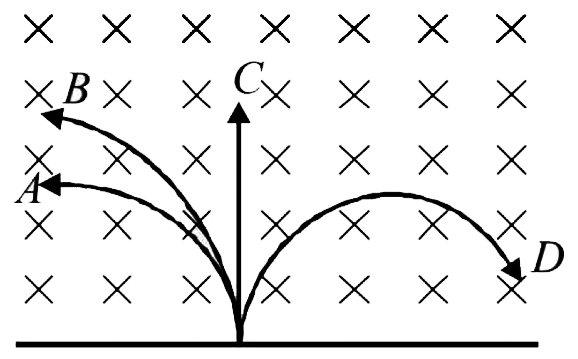
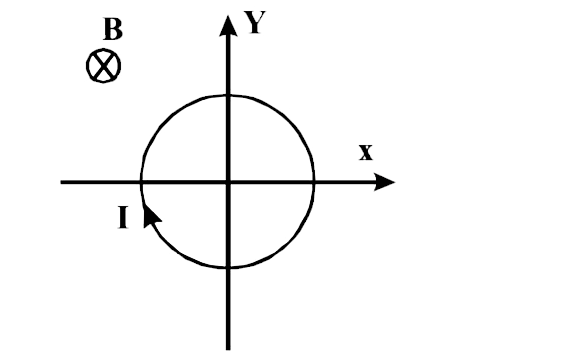
A neutron, a proton , and an electron and an alpha particle enter a region of constant magnetic field with equal velocities . The magnetic field is along the inward normal to the plane of the paper . The tracks of the particles are labelled in fig. the electron follows track .... and the alpha particle follows track.....
View SolutionA wire of length `L metre ` , carrying a current `I `ampere is bent in the form of a circle . The magnitude of its magnetic moment is …………. ` MKS units ` .
View SolutionIn a hydrogen atom , the electron moves in an orbit of radius ` 0.5 A` making `10^( 16 ) revolutions per second . The magnetic moment associtated with the orbital motion of the electron is ……
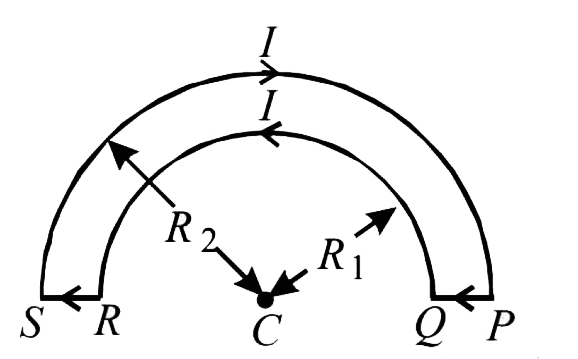
View SolutionThe wire loop `PQRSP` formed by joining two semicircular wires of radii ` R_(1)` and `R_(2)` carries a current `I` as shown . The magnitude of the magnetic induction at the center `C` is ………..
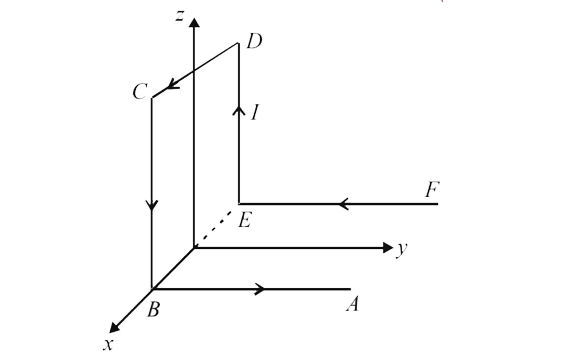
View SolutionA wire `ABCDEF` ( with each side of length `L`) bent as shown in figure and carrying a current `I` is placed in a uniform magnetic induction `B` parallel to the positive ` y- direction `. The force experienced by the wire is ……….. In the ………. direction .
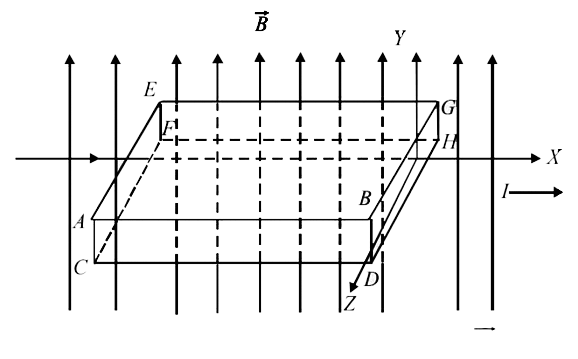
View SolutionA metallic block carrying current `I` is subjected to a uniform magnetic induction `vec(B) as shown in Figure . The moving charges experience a force ` vec(F) given by ….. Which results in the lowering of the potential of the face ……. Assume the speed of the carries to be `v` .
View SolutionNo net force acts on a rectangular coil carrying a steady current when suspended freely in a uniform magnetic field.
View SolutionThere is no change in the energy of a charged particle moving in a magnetic field although a magnetic force is acting on it .
View SolutionA charged particle enters a region of uniform magnetic field at an angle of ` 85@` to the magnetic line of force . The path of the particle is a circle .
View SolutionAn electron and a proton are moving with the same kinetic energy along the same direction . When they pass through a uniform magnetic field perpendicular to the direction of their motion , they describe circular paths of the same radius.
View SolutionA conducting circular loop of radiius `r` carries a constant current `i`. It is placed in a uniform magnetic field `vec(B)_(0)` such that `vec(B)_(0)` is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionA battery is connected between two points `A and B` on the circumference of a uniform conducting ring of radius `r` and resistance `R` . One of the arcs `AB` of the ring subtends an angle `theta` at the centre . The value of the magnetic induction at the centre due to the current in the ring is
View SolutionA proton , a deutron and `alpha )`- particle having the same kinetic energy are moving in circular trajectories in a constant magnetic field . If ` r_(p), r_(d) , and r_(alpha)` denote respectively the radii of the trajectories of these particles , then
View SolutionA circular loop of radius `R` , carrying `I`, lies in `x- y` plane with its origin . The total magnetic flux through ` x-y` plane is
View SolutionA charged particle is released from rest in a region of steady and uniform electric and magnetic fields which are parallel to each other . The particle will remove in a
View SolutionA particle of the charged `q` and `mass m` moves in a circular orbit of radius `r ` with angular speed ` omega` . The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionTwo long parallel wires are at a distance ` 2d` apart. They carry steady equal currents flowing out of the plane of the paper , as shown. The variation of the magnetic field `B` along the line `XX` is given by
View SolutionAn infinitely long conductor ` PQR` is bent to form a light angle as shown in Figure . A current `I` flows through `PQR` . The magnetic field due to this current at the point `M` is `H_(1)`. Now , another infinitely long straight conductor `QS` is connected at `Q` so that current is `(I)/(2)` in `QR` as well as in `QS` , the current in `PQ` remaining unchanged . The magnetic field at `M` is now `H_(2)`. The ratio `(H_(1))/(H_(2)` is given by
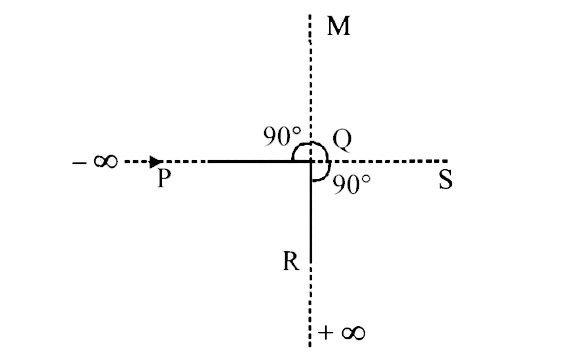
View SolutionAn ionized gas contains both positive and negative ions . If it is subjected simultaneously to an electric field along the ` +x` - direction and a magnetic field along the ` +y` - direction and the negative ions towardws `-y` - direction
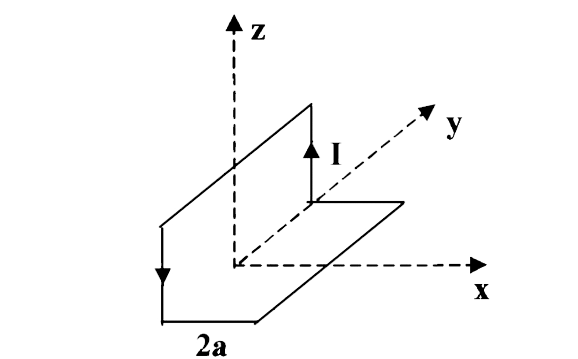
View SolutionA non - planar loop of conducting wire carrying a current `I` is placed as shown in the figure . Each of the straighrt sections of the loop is of the length ` 2a`. The magnetic field due to this loop at the point `P(a, 0 ,a)` points in the direction
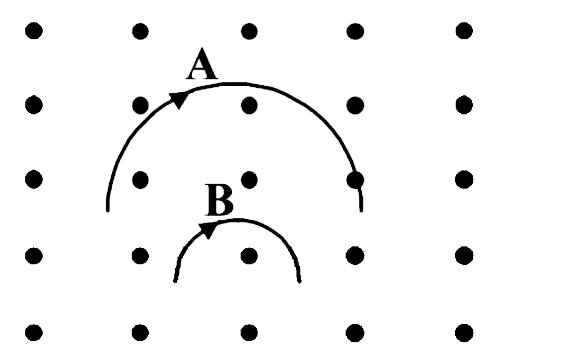
View SolutionTwo particles `A and B` of masses ` m_(A) and m_(B)` respectively and having the same charge are moving in a plane . The speeds of the particles are ` v_(A) and v_(B)` respectively and the trajectories are as shown in the figure. Then
View SolutionA coil of mass `m ` and charge ` q` moves with a constant velocity `v` along the positive `x - direction` . It enters a region containing a uniform magnetic field `B` directed along the negative ` z- direction` , extending from ` x =a to x = b`. The minimum value of `v` required so that the paRTICLE CAN JUST ENTER THE REGION `XgtB` IS
View SolutionA particle of the mass ` m ` and cgharge ` q` moves with a constant velocity `v` along the positive x- direction . It enters a region containing a uniform magnetic field `B` directed along the minimum value of `v` required so that the particle can just enter the region ` xgtb` is
View SolutionA long straight wire along the `z- axis` carries a current ` I` in the negative ` z- direction` . The magnetic vector field ` vec(B)` at a point having coordinates (x,y) in the ` Z = 0` plane is
View SolutionThe magnet field lines due to a bar magnet are correctly shown in
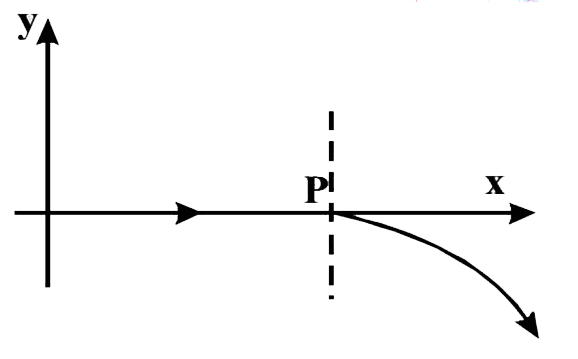
View SolutionFor a positively charged particle moving in a `x-y` plane initially along the `x-axis` , there is a sudden change in its path due to the presence of electric and//or magnetic fields beyond `p` . The curved path is shown in the ` x- y `plane and is found to be non - circular. Which one of the following combinations is possible ?
View SolutionA conducting loop carrying a current `I` is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to
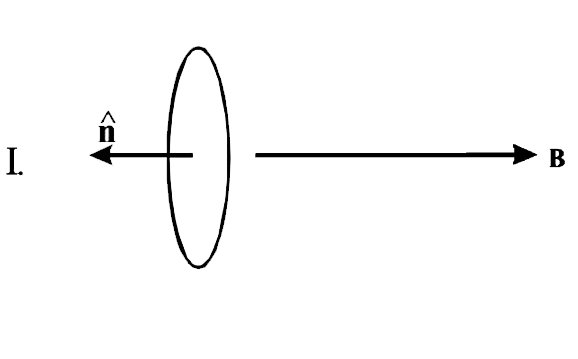
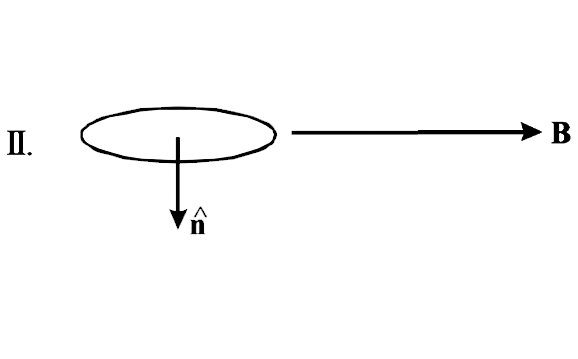
View SolutionA current carrying loop is placed in a uniform magnetic field in four different orientations , I,ii,iii & iv arrange them in the decreasing order of potential Energy`


View SolutionAn electron travelling with a spped `u` along the positive `x-axis` enters into a region of magnetic field where `B= - B_(0)hat (K) (xgt0)`. It comes out of the region with speed `v` then

View SolutionA magnetic field ` vec(B) = B_(0)hat(j)` , exists in the region `a ltxlt2a` , and `vec(B) = -B_(0) hat(j)` , in the region `2a lt xlt 3a`, where `B_(0)` is a positive constant . A positive point charge moving with a velocity `vec(v) = v_(0) hat (i)` , where `v_(0)` is a positive constant , enters the magnetic field at `x= a` . The trajectory of the charge in this region can be like

View SolutionA thin flexible wire of length `L` is connected to two adjacent fixed points carries a current `I` in the clockwise direction, as shown in the figure.When system is put in a uniform magnetic field of strength `B` going into the plane of paper, the wire takes the shape of a circle.The tension in the wire is:

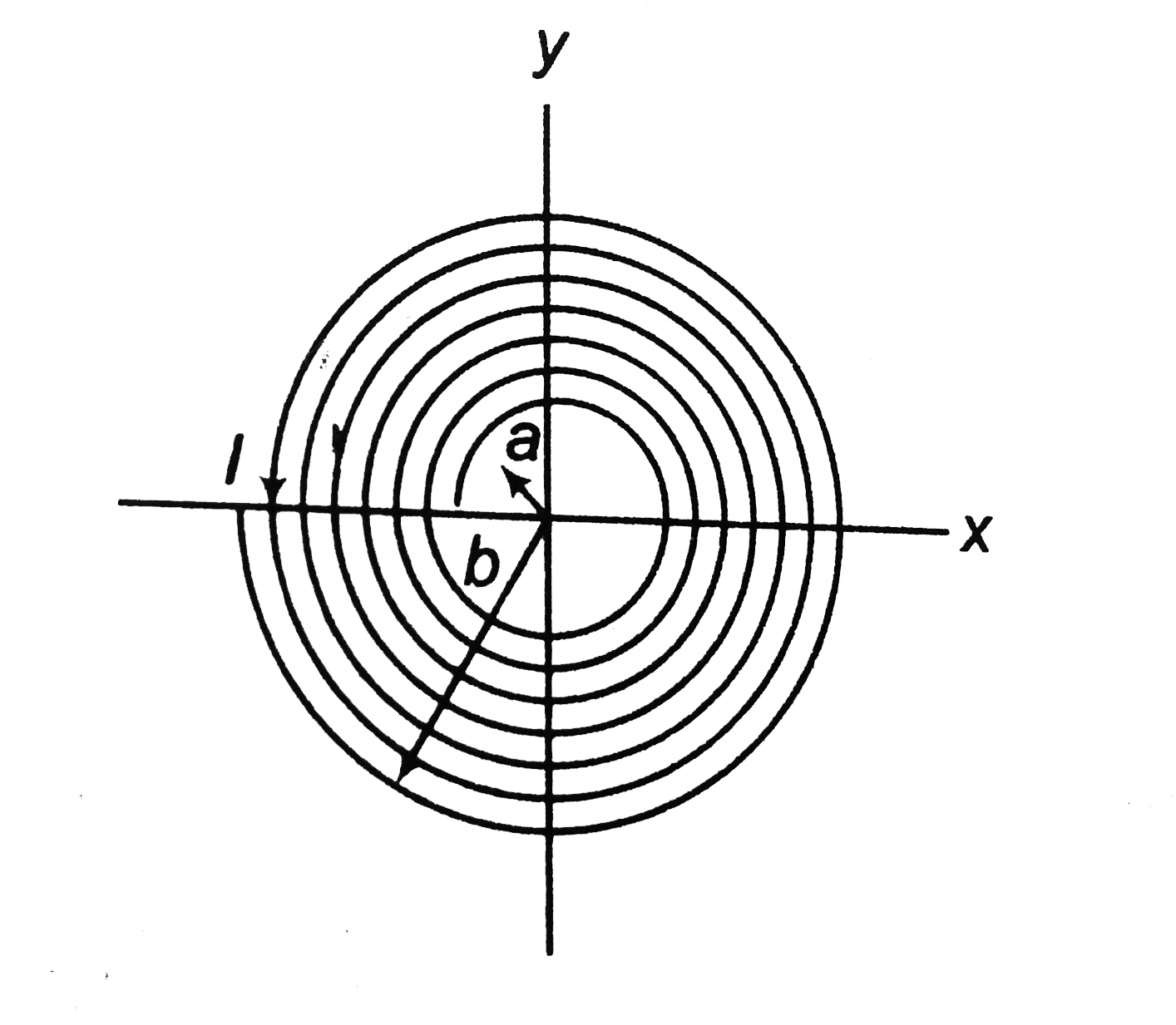
View SolutionA long insulated copper wire is closely wound as a spiral of `N` turns. The spiral has inner radius a and outer radius `b`. The spiral lies in the `xy`-plane and a steady current I flows through the wire. The`z`-component of the magetic field at the centre of the spiral is
View SolutionA loop carrying current `I` lies in the ` x-y ` plane as shown in the figure . The unit vector ` hat k` is coming out of the plane of the paper . The magnetic moment of the current loop is
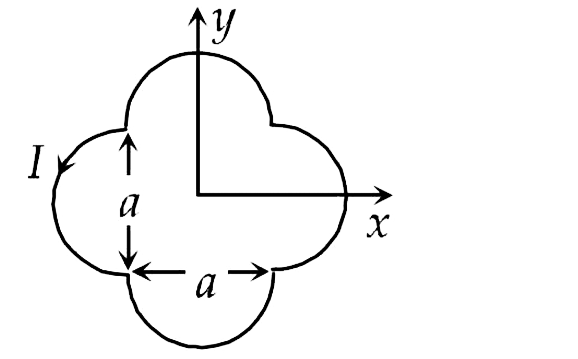
View SolutionAn infinitely long hollow conducting cylinder with inner radius `(R )/(2)` and outer radius `R` carries a uniform current ra density along its length . The magnitude of the magnetic field , ` | vec(B)|` as a function of the radial distance `r` from the axis is best represented by
View SolutionA magnetic needle is kept in a non uniform magnetic field . It experiences
View SolutionA charged paricle goes undeflected in a region containing electric and magnetic field. It is possible that
View SolutionA rectangular loop carrying a current ` i` is situated near a long straight wire such that the wire is parallel to one of the sides of the loop and is in the plane of the loop . If steady current ` I` is established in the wire as shown in the figure ,
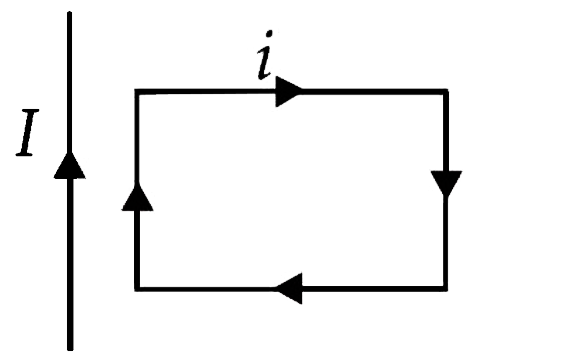
View SolutionTwo thin long parallel wires seperated by a distance 'b' are carrying a current ' I' amp each . The magnitude of the force3 per unit length exerted by one wire on the other is
View SolutionTwo particle X and Y having equal charge, after being accelerated through the same potential difference enter a region of uniform magnetic field and describe circular paths of radii `R_1 and R_2` respectively. The ratio of the mass of X to that of Y is
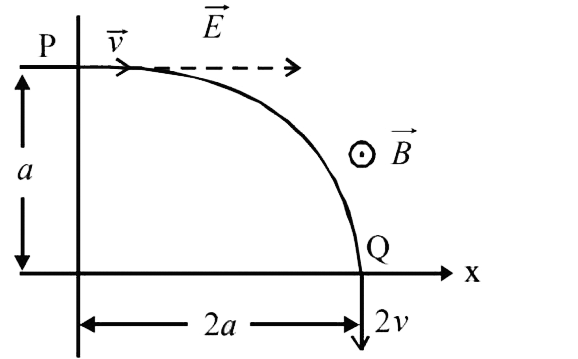
View SolutionA particle of charge ` +q` and mass `m` moving under the influence of a uniform electric field ` E hat(i)` and uniform magnetic field ` B hat(k)` follows a trajectory from ` P to Q` as shown in fig. The velocities at `P and Q` are ` v hat(i)` and ` - 2v hat(j)` . which of the following statement(s) is/are correct ?
View SolutionA microameter has a resistance of `100 omega and a full scale range of ` 50 muA`. It can be used as a voltmeter or as a higher range ammeter provides a resistance is added to it . Pick the correct range and resistance combination(s)
View SolutionA current ` I` flows along the length of an infinitely long, straight , thin - walled pipe. Then
View Solution` H^(+), He^(+) and O^(++)` all having the same kinetic energy pass through a region in which there is a uniform magnetic field perpendicular to their velocity . The masses of ` H^(+), He^(+) and O^(2+)` are `1 amu, 4 amu and 16 amu` respectively . Then
View SolutionTwo particles , each of mass ` m` and charge `q`, are attached to the two ends of a light rigid rod of length ` 2 R` . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionTwo very long, straight , parallel wires carry steady currents ` I &-I` respectively . The distance between the wires is `d`. At a certain instant of time, a point charge `q` is at a point equidistant from the wires , in the plane of the wires. Its instantaneous vel,ocity ` v` is perpendicular to this plane. The magnitude of the force due to the magnetic field acting on the charge at this instant is
View SolutionThe following field line can never respresent

View SolutionA particle of mass `m`and charge `q`, moving with velocity `v` enters Region `II` normal to the boundary as shown in the figure. Region `II` has a uniform magnetic field `B` perpendicular to the plane of the paper . The length of the region `II` is `l`. Choose the correct choice(s).

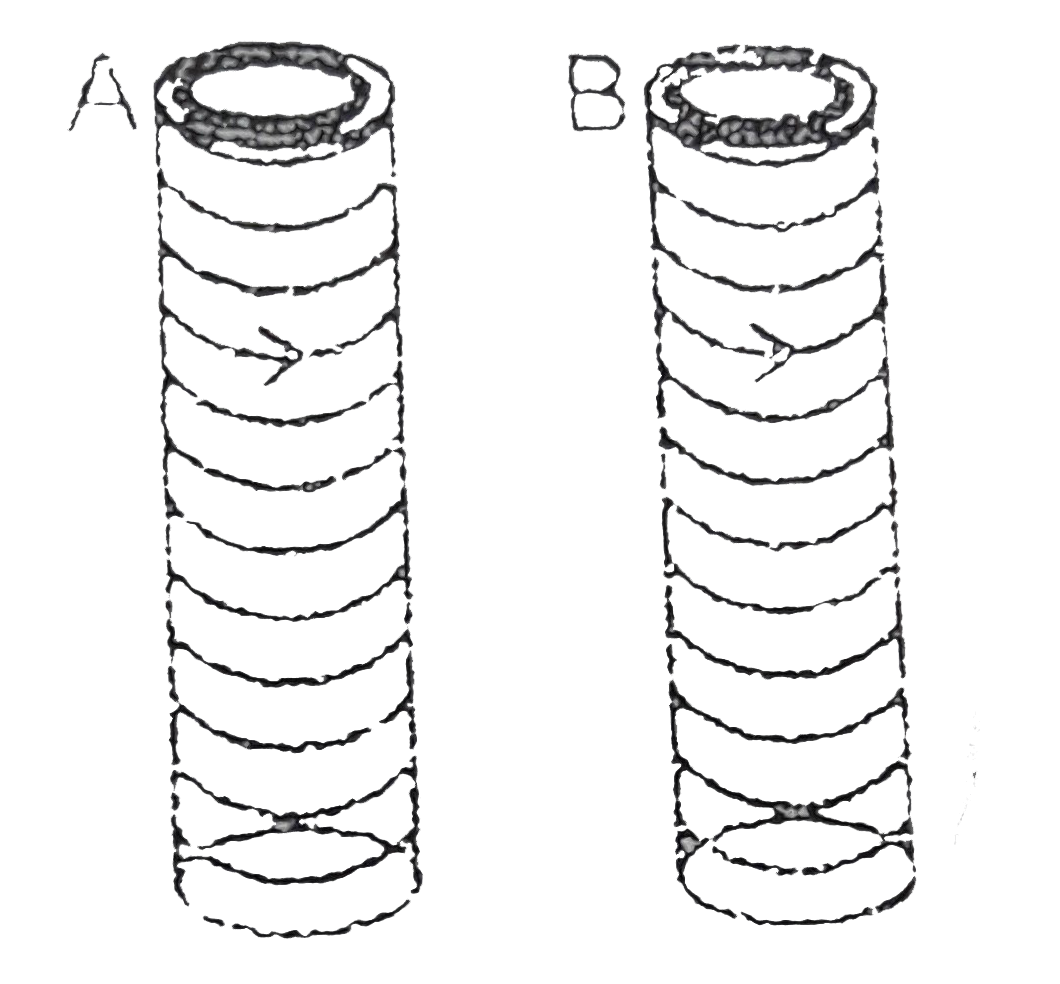
View SolutionTwo metallic rings `A` and `B` identical in shape and size but having different resistivities `rho_(A)` and `rho_(B)` are kept on top of two idential solenoids as shown in the figure.When current `I` is switched on in both the solenoids in identical manner, the rings `A` and `B` jump to heights `h_(A)` and `h_(B)` respectively with `h_(A)` gt `h_(B)`. The possible relation(s) between their resistivities and their masses `m_(A)` and `m_(B)` is (are)
View SolutionAn electron and a proton are moving on straight parallel paths with same velocity. They enter a semi infinite region of uniform magnetic field perpendicular to the velocity.
Which of the following statement(s) is /are true?
View SolutionConsider the motion of a positive point charge in a region where area simultaneous uniform electric and magnetic fields ` vec(E) = E_(0) hat(j)` and ` vec(B) = B_(0) hat(j)`. At time ` t = 0` , this charge has velocity ` vec(v)` in the ` x-y `plane , making an angle ` theta` with the ` x-axis `. Which of the following option(s) is (are) correct for time ` t gt 0`?
View SolutionA particle of mass`M` and positive charge `Q`, moving with a constant velocity ` vec(u_(1)) = 4 hat(i) ms^(-1)`, enters a region of uniform static magnetic field , normal to the ` x-y ` plane. The region of the magnetic field extends from ` x= 0` to ` x = L` for all values of `y`. After passing through this region, the particle emerges on the other side after 10 milliseconds with a velocity `vec(u_(2)) = 2 (sqrt3 hat(i) + hat(j))) ms^(-1)` . The correct statement(s) is (are)
View SolutionA steady current `I` flows along an infinitely long hollow cylindrical conductor of radius `R`. This cylinder is placed coaxially inside an infinite solenoid of radius `2 R`. The solenoid has a `n` turns per unit length and carries a steady current `I`. Consider a point `p` at a distance `r` from the common axis . The correct statement(s) is (are)
View SolutionA conductor (shown in the figure) carrying constant current `I` is kept in the `x-y` plane in a uniform magnetic field ` vec(B)`. If ` vec(F)` is the magnitude of the total magnetic force acting on the conductor, then the correct statement(s) is (are)
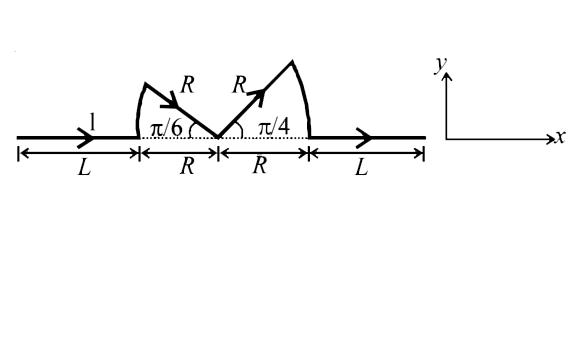
View SolutionConsider two identical galvanometers and two identical resistors with resistance `R`. If the internal resistance of the galvanometers `R_(c) lt R//2`, which of the following statement(s) about any one of the galvanometers is (are) true?
View SolutionA bar magnet with poles ` 25 cm` apart and of strength `14.4 amp - m` rests with centre on a frictionless pivot. It is held in equilibrium aat an angle of ` 60@` with respect to a uniform magnetic field of induction `0.25 Wb//m^(2)` , by applying a force `F` at right angles to its axis at a point `12 cm` from pivot. Calculate `F`. What will happen if the force `F` is removed?
View SolutionA bar magnet is placed with its north pole pointing north and its south pole pointing south. Draw a figure to show the location of neutral points .
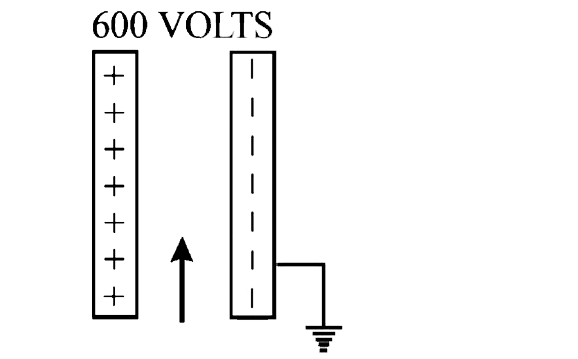
View SolutionA potential difference of `600 volts` is applied across the plates of a parallel plate consenser . The separation between the plates is `3mm`. An electron projected vertically, parallel to the plates , with a velocity of `2 xx 10^(6) m//sec` moves underflected between the plates. Find the magnitude and direction of the magnetic field in the region between the condenser plates. ( Neglect the edge effects). Charge of the electron = `-1.6xx10^(-19)` coulomb
View SolutionA particle of mass `m = 1.6 X 10^(-27)` kg and charge `q = 1.6 X 10^(-19)` C moves at a speed of `1.0 X10^7 ms^(-1)`. It enters a region of uniform magnetic field at a point E, as shown in The field has a strength of 1.0 T. (a) The magnetic field is directed into the plane of the paper. The particle leaves the region of the filed at the point F. Find the distance EF and the angle theta. (b) If the field is coming out of the paper, find the time spent by the particle in the regio the magnetic feld after entering it at `E`.

View SolutionA beam of protons with a velocity of `4 X 10 ^5 ms^(-1)` enters a uniform magnetic field of 0.3 T. The velocity makes an angle of `60^@` with the magnetic field. Find the radius of the helicla path taken by the proton beam and the pitch of the helix.
View SolutionTwo long, straight wires a and b are `2*0` m apart, perpendicular to the plane of the paper as shown in figure . The wire a carries a current of `9*6 A` directed into the plane of the figure,The magnetic field at the point P at a distance of 10/11 m from the wire b is zero.
Find (a) the magnitude and direction of the current in b,
(b) the magnitude of the magnetic field B at the point s
(c) the force per unit length on the wire b`.
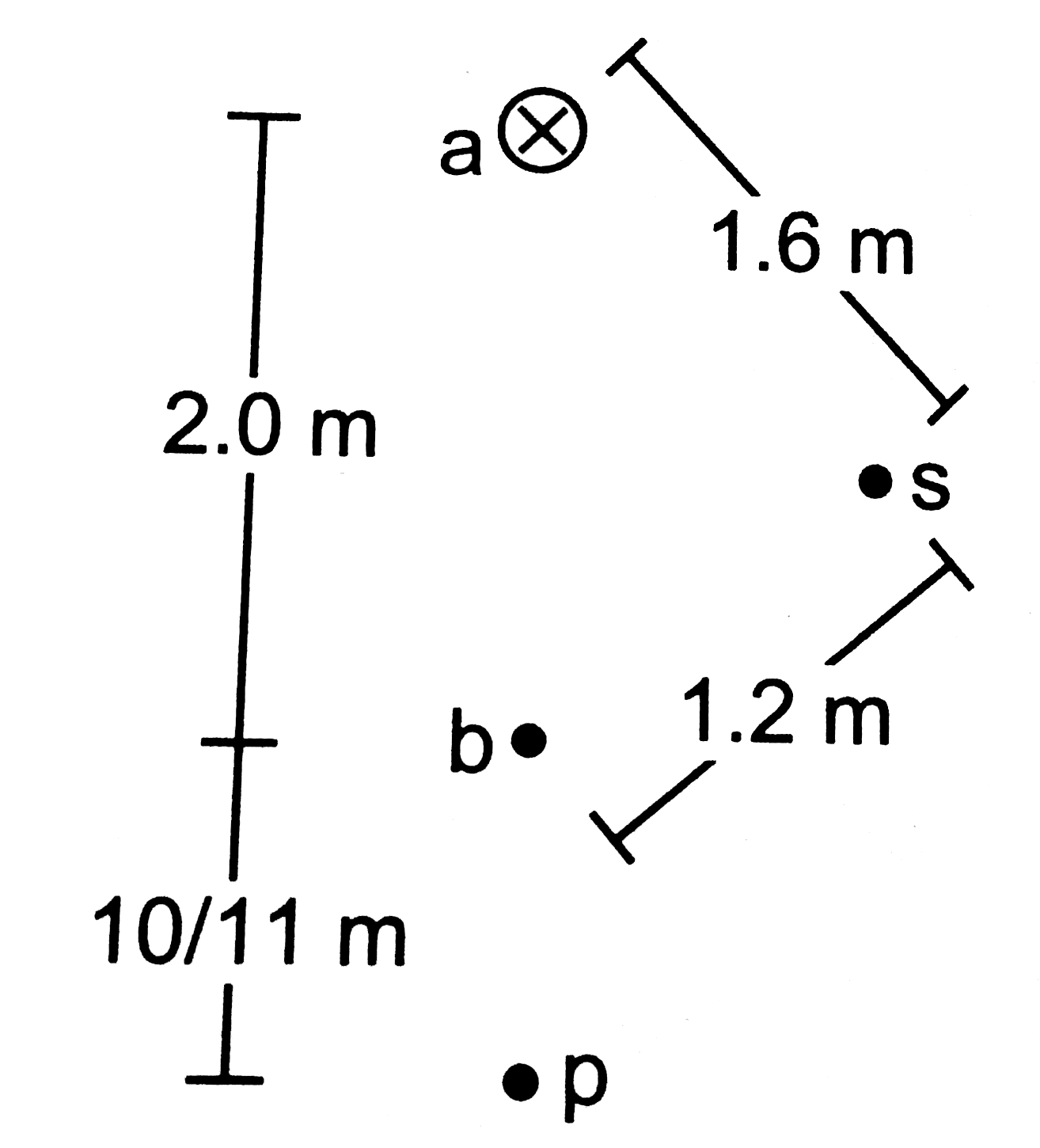
View SolutionA pair of stationary and infintely long bent wires are placed in the ` XY` planes as shown in fig. The wires carry currents of ` I = 10 amperes` each as shown . The segments `P and Q` are parallel to the ` Y-axis` such that ` OS = OR = 0.02 m`. Find the magnitude and direction of the magnetic induction at the origin `O`.
View SolutionTwo long parallel wires carrying current ` 2.5 amperes` and `I ampere` in the same direction ( directed into the plane of the paper) are held at `P and Q` respectively such that they are perpendicular to the plane of paper. The points `P and Q` are located at a distance of ` 5 metres and 2 metres` respectively from a collinear point `R` ( see figure)
(i) An electron moving with a velocity of ` 4xx10^(5) m//s ` along the positive ` x- direction ` experiences a force of magnitude `3.2xx10^(-20) N` at the point `R`. Find the value of `I`.
(ii) Find all the positions at which a third long parallel wire carrying a current of magnitude `2.5 amperes` may be placed so that the magnetic induction at `R` is zero.
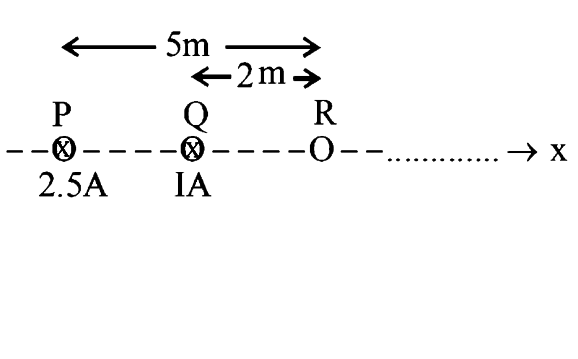
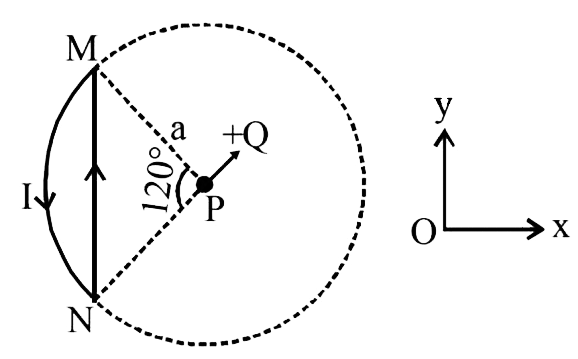
View SolutionA wire loop carrying `I` is placed in the ` x-y`plane as shown in fig.
(a) If a particle with charge ` +Q` and mass `m` is placed at the centre `P` and given a velocity ` vec(v)` along `NP`(see figure), find its instantaneous acceleration.
( b) If an external uniform magnetic induction field ` vec(B) = Bhat(i)` is applied , find the force and the torque acting on the loop due to this field.
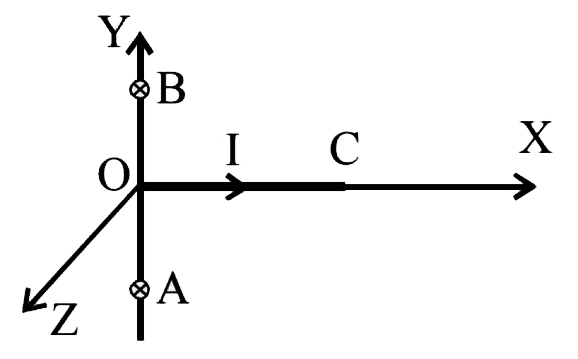
View SolutionA straight segment `OC`(of length L meter) of a circuit carrying a current `I amp` is placed along the ` x- axis` ( fig.). Two infinetely long straight wires ` A and B` , each extending from ` z = -oo to +oo`, are fixed at ` y = -ameter and y = +a meter` respectively, as shown in the figure.
If the wires ` A and B` each carry a current `I amp` into the plane of the paper, obtain the expression for the force acting on the segment ` OC`. What will be the force on `OC` if the current in the wire `B` is reversed?
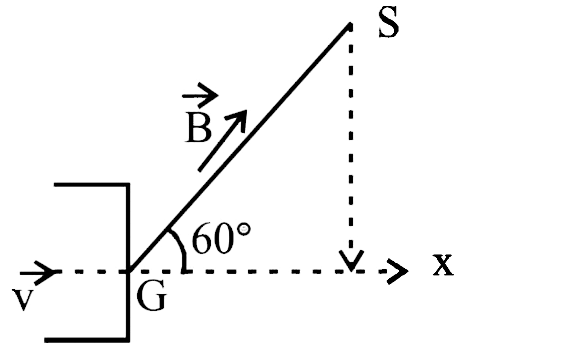
View SolutionAn electron gun ` G` emits electrons of energy `2ke V` travelling in the positive ` x- direction` . The electrons are required to hit the spot `S` where `GS = 0.1m`, and the line `GS` makes an angle of `60^(@)` with the ` x-axis` as shown in the fig. A uniform magnetic field `vec(B)` parallel to `GS` exists in the region outside the electron gun. Find the `GS` exists in the region outside the electron gun. Find the minimum value of `B` needle to make the electron hit `S`.
View SolutionA long horizontal wire `AB`, which is free to move in a vertical plane and carries a steady current of `20 A`, is in equilibrium at a height of `0.01 m` over another parallel long wire `CD` which is fixed in a horizontal plane and carries a steady current of ` 30 A`, as shown in figure. Shown that when `AB` is slightly depressed, it executes simple harmonic motion. Find the period of oscillations.

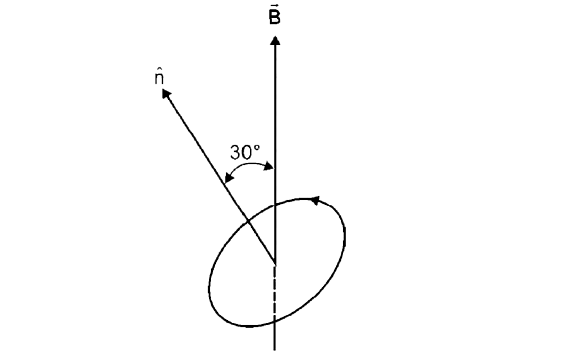
View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius `R`.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction `vec(B)` such that the plane - normal of the electron - orbit makes an angle of ` 30^(@)` with the magnetic induction . Find the torque experienced by the orbiting electron.
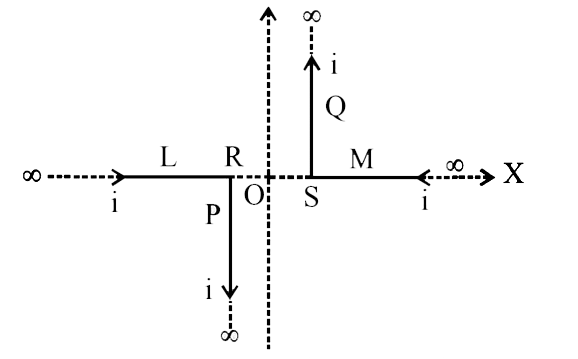
View SolutionThree infinitely long thin wires, each carrying current `i` in the same direction, are in the `x-y` plane of a gravity free space . The central wire is along the `y - axis` while the other two are along `x = +-d`.
(i) Find the locus of the points for which the magnetic field `B` is zero.
(ii) If the central wire is displaced along the ` Z- direction` by a small amount and released, show that it will excecute simple harmonic motion . If the linear density of the wires is `lambda`, find the frequency of oscillation.
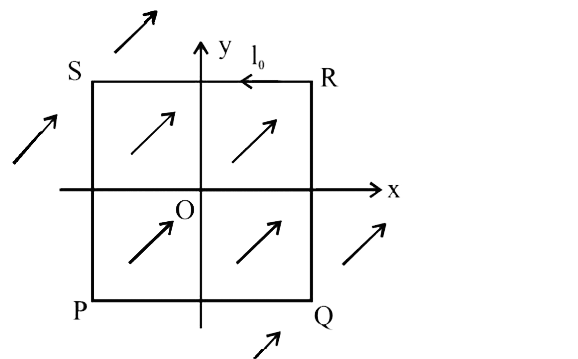
View SolutionA uniform constant magnetic field `B` is directed at an angle of `45^(@)` to the `x axis` in the ` xy`- plane . ` PQRS` is a rigid, square wire frame carrying a steady current `I_(0)`, with its centre at the origin `O`. At time ` t = 0`, the frame is at rest in the position as shown in figure , with its sides parallel to the ` x and y` axis. Each side of the frame is of mass `M` and length `L`.
(a) What is the torque `tau` about `O` acting on the frame due to the magnetic field?
(b) Find the angle by which the frame rotates under the action of this torque in a short interval of time `Deltat`, and the axis about this rotation occurs .`(Deltat)` is so short that any variation in the torque during this interval may be neglected
Given : the moment of interia of the frame about an axis through its centre perpendicular to its about an axis through its centre perpendicular to its plane is `(4)/(3) ML^(2)`.
View SolutionThe region between ` x=o and x = L` is filled with uniform, steady magnetic field `B_(0) hat(k)`. A particle of mass `m` , positive charge `q` and velocity `v_(0) hat(i)` travels along ` x-axis` and enters the region of the magnetic field. Neglect gravity throughout the question .
(a) Find the value of `L` if the particle emerges from the region of magnetic field with its final velocity at angle `30^(@)` to its initial velocity.
(b) Find the velocity of the particle and the time spent by it in the magnetic field, if the magnetic field now extends upto `2.1L`.
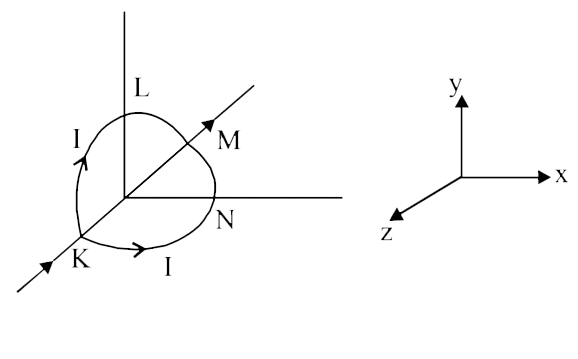
View SolutionA circular loop of radius `R` is bent along a diameter and given a shapes as shown in the figure. One of the semicircles `(KNM)` lies in the ` x-z` plane with their centres and the other one `(KLM)` in the `y-z` plane with their centres at the origin. current `I` is flowing through each of the semi circles as shown in figure.
(a) A particle of charge `q` is released at the origin with a velocity `vec(v) = -v_(0)hat(i)`. Find the instantaneous force `vec(F)` on the particle . Assume that space is gravity free.
(b) If an external uniform magnetic field `B_(0) hat(j) ` is applied , determine the force `vec(F)_(1) and vec(F)_(2)` on the semicircles `KLM and KNM` due to the field and the net force ` vec(F)` on the loop.
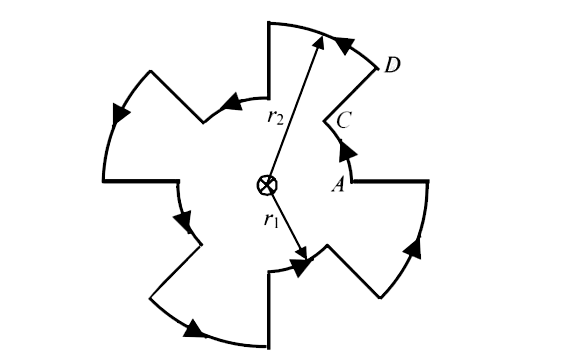
View SolutionA current of `10 A` flows around a closed path in a circuit which is in horizontal plane as shown in the figure . The circuit consists of eight alternating arcs of ` radii r_(1) = 0.08 m and r_(1) = 0.12 m`. Each arc subtends the same at he center.
(a) Find the magnetixc field produced by this circuit at the center.
(b) An infinitely long straight wire carrying a current of `10 A` is passing through the center of the above circuit vertically with the direction of the current being into the plane of the circuit . What is the force acting on the arc `AC` and the straight segment ` CD` due to the current at the center?
View SolutionA wheel of radius ` R` having charg `Q`, uniformly distributed on the rim of the wheel is free to rotate about a light5 horizontal rod. The rod is suspended by light inextensible strings and a magnetic field `B` is applied as shown in the figure. The initial tensions in the strings are `T_(0)`. If the breaking tension of the strings are `(3T_(0))/(2)`, find the maximum angular velocity `omega_(0)` with which the wheel can be rotated.
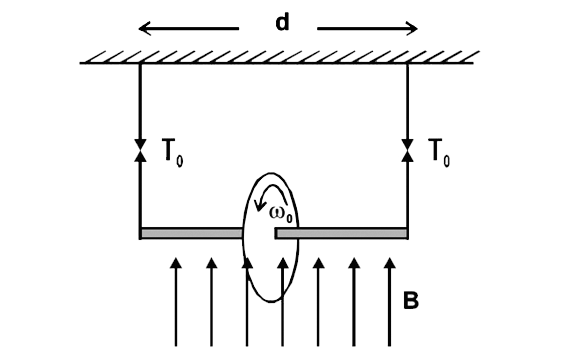
View SolutionA proton and alpha - particle are accelerated with same potential difference and they enter in the region of constant magnetic field `B` perpendicular to the velocity of particles. Find the ratio of radius of curvature of alpa - particle.
View SolutionIn a moving coil galvanometer, torque on the coil can be experessed as `tau = ki`, where `i` is current through the wire and `k` is constant . The rectangular coil of the galvanometer having number of turns `N` , area `A` and moment of interia `I` is placed in magnetic field `B`. Find
(a) `k` in terms of given parameters `N,I,A andB`
(b) the torsion constant of the spring , if a current `i_(0)` produces a deflection of `(pi)//(2)` in the coil .
(c) the maximum angle through which the coil is deflected, if charge `Q` is passed through the coil almost instaneously. ( ignore the daming in mechinal oscillations).
View SolutionAdvanced countries are making use of powerful electromagnets to move trains at very high speed. These trains are called maglev trains (abbreviated from magnetic levitation).These trains float on a guideway and do not run on steel rail tracks.
Instead of using a engine based on fossil fuels, they make use of magnetic field forces. The magnetized coils are arranged in the guide way which repels the strong magnets placed in the train's under carriage. This helps train move over the guideway, a technic called electro - dynamic suspension. When current passes in the coils of guideway , a typical magnetic field is set up between the undercarriage of train and guideway which pushes and pull the train along the guideway depending on the requirement.
The lack of friction and its aerodynamic style allows the train to more at very high speed.
(i) The levitation of the train is due to
View SolutionAdvanced countries are making use of powerful electromagnets to move trains at very high speed. These trains are called maglev trains (abbreviated from magnetic levitation).These trains float on a guideway and do not run on steel rail tracks.
Instead of using a engine based on fossil fuels, they make use of magnetic field forces. The magnetized coils are arranged in the guide way which repels the strong magnets placed in the train's under carriage. This helps train move over the guideway, a technic called electro - dynamic suspension. When current passes in the coils of guideway , a typical magnetic field is set up between the undercarriage of train and guideway which pushes and pull the train along the guideway depending on the requirement.
The lack of friction and its aerodynamic style allows the train to more at very high speed.
(2) The disadvantage of maglev trains is that
View SolutionAdvanced countries are making use of powerful electromagnets to move trains at very high speed. These trains are called maglev trains (abbreviated from magnetic levitation).These trains float on a guideway and do not run on steel rail tracks.
Instead of using a engine based on fossil fuels, they make use of magnetic field forces. The magnetized coils are arranged in the guide way which repels the strong magnets placed in the train's under carriage. This helps train move over the guideway, a technic called electro - dynamic suspension. When current passes in the coils of guideway , a typical magnetic field is set up between the undercarriage of train and guideway which pushes and pull the train along the guideway depending on the requirement.
The lack of friction and its aerodynamic style allows the train to more at very high speed.
(3) The force which makes maglev move
View SolutionThe figure shows a circular loop of radius `a` with two long parallel wires `(numbered 1 and 2)` all in the plane of the paper . The distance of each wire from the centre of the loop is `d`. The loop and the wire are carrying the same current `I`. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at `P` due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at `P`.
(s) The wires repel each other.
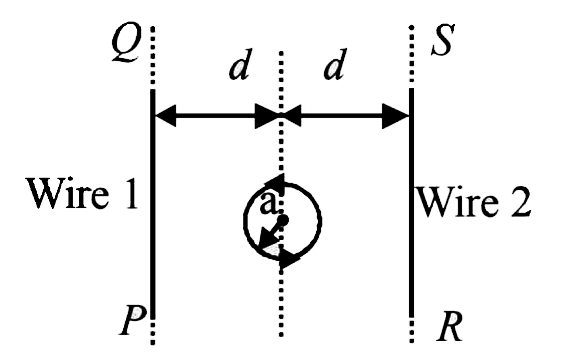
(4) When `d~~a` but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that case
View SolutionThe figure shows a circular loop of radius `a` with two long parallel wires `(numbered 1 and 2)` all in the plane of the paper . The distance of each wire from the centre of the loop is `d`. The loop and the wire are carrying the same current `I`. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at `P` due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at `P`.
(s) The wires repel each other.

(4) When `d~~a` but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that case
View SolutionIn a thin rectangular metallic strip a constant current `I` flows along the positive `x`-direction , as shown in the figure. The length , width and thickness of the strip are `l, w and d`, respectively.
A uniform magnetic field `vec(B)` is applied on the strip along the positive `y- direction` . Due to this, the charge carriers experience a net deflection along the `z- direction` . This results in accumulation of charge carriers on the surface `PQRS` ansd apperance of equal and opposite charges on the face opposite to `PQRS`. A potential difference along the `z-direction` is thus developed. Charge accumulation contiues untill the magnetic force is balanced by the electric force. The current is assumed to be uniformly distributed on the cross- section of the strip and carried by electrons.
Consider two different metallic strips `(1 and 2)` of the same material . Their lengths are the same,widths are `w_(1) and w_(2)` and thickness are `d_(1) and d_(2)` respectively. Two points `K and M` are symmetrically located on the opposite faces parallel to the ` x-y` plane ( see figure) . `V_(1) and V_(2)` are the potential differences between `K and M` in strips ` 1 and 2`, respectively . Then, for a given current `I` flowing through them in a given magnetic field strength `B`, the correct statement(s) is (are)
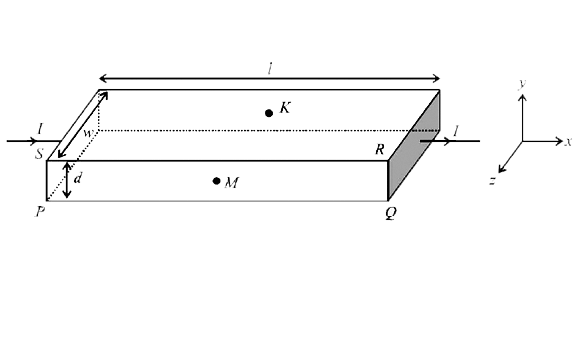
View SolutionIn a thin rectangular metallic strip a constant current `I` flows along the positive `x-`direction , as shown in the figure. The length , width and thickness of the strip are `l, w and d`, respectively.
A uniform magnetic field `vec(B)` is applied on the strip along the positive `y- direction` . Due to this, the charge carriers experience a net deflection along the `z- direction` . This results in accumulation of charge carriers on the surface `PQRS` ansd apperance of equal and opposite charges on the face opposite to `PQRS`. A potential difference along the `z-direction` is thus developed. Charge accumulation contiues untill the magnetic force is balanced by the electric force. The current is assumed to be uniformly distributed on the cross- section of the strip and carried by electrons.
Consider two different metallic strips `(1 and 2)` of same dimensions `n_(1) and n_(2)`, repectrively . Strip 1 is placed in magnetic field `B_(1)` and strip 2 is placed in magnetic field `B_(2)` , both along positive ` y- directions`. Then ` V_(1) and V_(2)` are the potential differences developed between `K and M` in strips 1 and 2 , respectively . Assuming that the current `I` is the same for both the strips, the correct option(s) is (are)
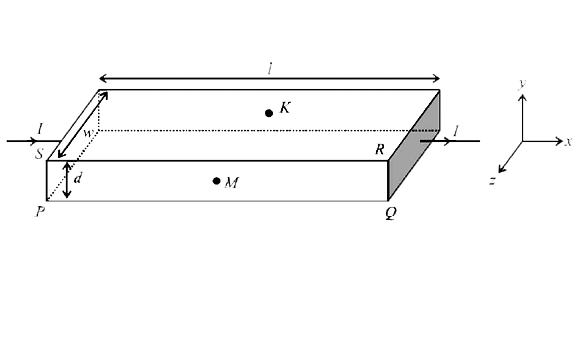
View SolutionStatement -1 : The sensitvity of a moving coil galvanometer is increased by placing a suitable magnetic material as a core inside the coil.
Statement - 2: Soft iron has a high magnetic permeability and cannot be easily magnetized or demagnetized.
View SolutionA steady current `I` goes through a wire loop `PQR` having shape of a right angle triangle with `PQ = 3x, PR = 4x and QR = 5x`. If the magnitude of the magnetic field at `P` due to this loop is `k((mu_(0)I)/(48 pi x))`, find the value of `K`.
View SolutionA long circular tube of length `10 m` and radius ` 0.3 m` carries a current `I` along its curved surface as shown . A wire - loop of resistance `0.005 ohm` and of radius `0.1 m` is placed inside the tube its axis coinciding with the axis of the tube . The current varies as `I = I_(0)cos(300 t)` where `I_(0)` is constant. If the magnetic moment of the loop is `Nmu_(0)I_(0) sin (300 t)`, then 'N' is
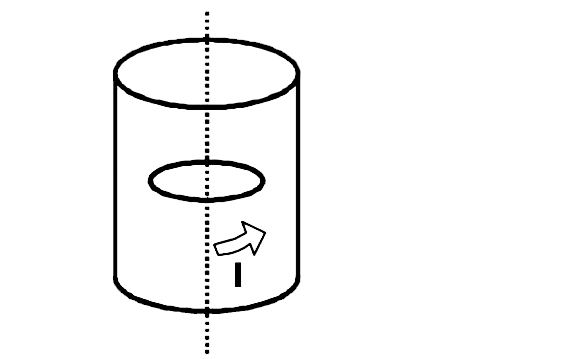
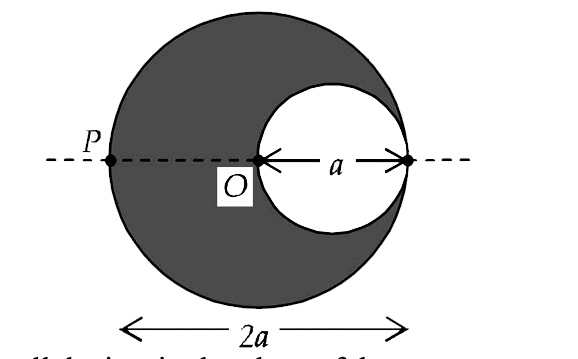
View SolutionA cylindrical cavity of diameter a exists inside a cylinder of diameter `2a` as shown in the figure. Both the cylinder and the cavity are infinitity long. A uniform current density `j` flows along the length . If the magnitude of the magnetic field at the point `P` is given by `(N)/(12) mu_(0)aJ`, then the value of `N` is
View SolutionTwo parallel wires in the plane of the paper are distance `X_(0)` apart. A point charge is moving with speed `u` between the wires in the same plane at a distance `X_(1)` from one of the wires. When the wires carry current of magnitude `I` in the same direction , the radius of curvature of the path of the point charge is `R_(1)`. In contrast, if the currents I in the two wires have directions opposite to each other, the radius of curvature of the path is `R_2`. if `(X_(0))/(X_(1)) = 3`, the value of `( R _(1))/( R_(2))` is
View SolutionIf in circular coil of radius `R`, current `I` is flowing and in another coil `B` of radius `2R` a current `2I` is flowing , then the raatio of the magnetic fields `B_(A) and B_(B)`, produced by them will be
View SolutionIf an electron and a proton having same momenta enter perpendicular to a magnetic field, then
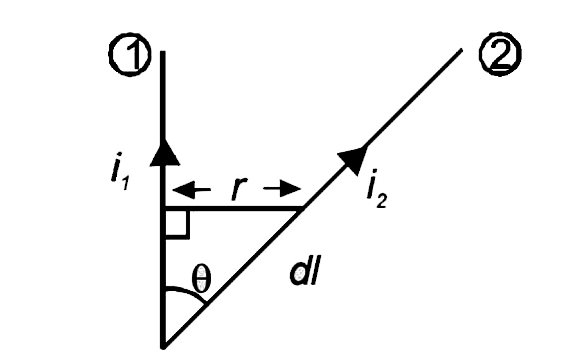
View SolutionWires `1 and 2` carrying currents `i_(1) and i_(2)` respectively are inclined at an angle `theta ` to each other. What is the force on a small element `dl` of wire `2` at a distance of `r` from wire 1 ( as shown in figure) due to the magnetic field of wire 1`?
View SolutionThe time period of a charged particle undergoing a circular motion in a uniform magnetic field is independent of its
View SolutionA particle of mass `M` and charge `Q` moving with velocity `vec(v)` describe a circular path of radius `R` when subjected to a uniform transverse magnetic field of induction `B`. The work done by the field when the particle completes one full circle is
View SolutionA particle of charge `-16xx10^(-18) coulomb` moving with velocity `10 ms^(-1)` along the ` x- axis `, and an electric field of magnitude `(10^(4))//(m)` is along the negative ` z- ais`. If the charged particle continues moving along the ` x- axis` , the magnitude of `B` is
View SolutionA thin rectangular magnet suspended freely has a period of oscillation equal to `T` . Now it is broken into two equal halves (each having half of the original length) and one piece is made to oscillate freely in the same field. If its period of made to oscillate freely in the same field. if its period of oscillation is 'T' , the ratio `(T')/(T)` is
View SolutionA magnetic needle lying parallel to a magnetic field requires `W units` of work to turn it through `60^(@)`. The torque needed to maintain the needle in this position will be
View Solutionthe magnetic lines of force inside a bar magnet
View SolutionCurie temperature is the temperature above which
View SolutionA current ` I` flows along the length of an infinitely long, straight , thin - walled pipe. Then
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is `B`. It is then bent into a circular loop of `n` turns. The magnetic field at the centre of the coil will be
View SolutionThe magnetic field due to a current carrying loop of radius ` 3 cm` at a point on the axis at a distance of `4 cm` from the centre is ` 54 muT`. What will be its value at the centre of loop ?
View Solution
JEE Main And Advanced questions and complete solutions for chapter MOVING CHARGES AND MAGNETISM of SUNIL BATRA 41 YEARS IITJEE PHYSICS (HINGLISH) of Class 12