A cylindrical cavity of diameter a exists inside a cylinder of diameter 2a as shown in the figure. Both the cylinder and the cavity are infinitity long. A uniform current density j flows along the length . If the magnitude of the magnetic field at the point P is given by N12μ0aJ, then the value of N is
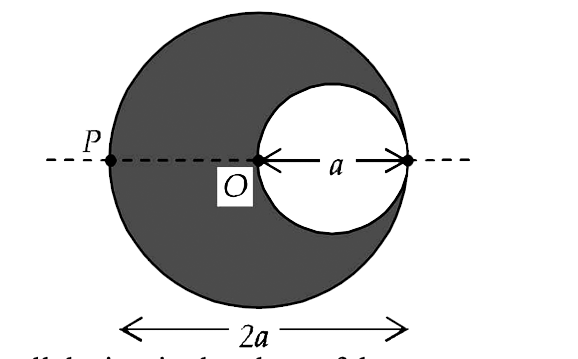
Current dwensity J=currentarea=Iπ(2a2)=I'(πa2)
rArr I=(I')=I4
Let us consider the cavity to have current I') flowing in both the directions.
the magnetic field at P due to the current flowing through the cylinder
B1=μ04π2Ia
The magnetic field at P due to the current (I') flowing in opposite direction is
B2=μ04π3I'3a/2=μ04π2(I/4)3a/2=μ04πI3a
:. The net magnetic field is
B=B1−B2=μ04πIa[2−13]=μ04πIa×53<br>∴(B = mu_(0))/( 4 pi) (J pi a^(2))/(a)xx(5)/(3) = mu_(0) ( 5 Ja)/(12)
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - MCQs(d )
1 Videos
- MODERN PHYSICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MODERN PHYSICSEXERCISE - MCQ (One Correct Answer
1 Videos
- RAY AND WAVE OPTICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - RAY AND WAVE OPTICSEXERCISE - JEE Main And Advanced
209 Videos
Similar Questions
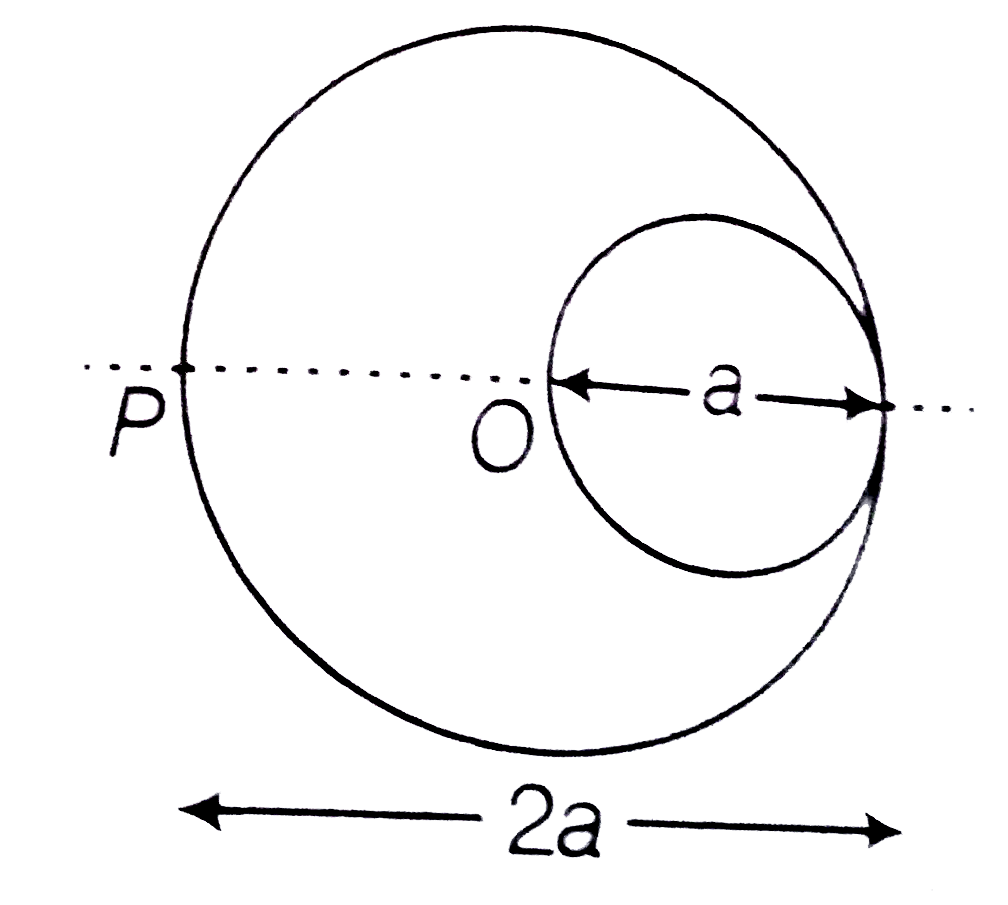
A cylinderical cavity of diameter a exists inside a cylinder of diameter 2a as shown in the figure. Both the cylinder and the cavity are infinitely long. A uniform current density J flows along the length. If the magnitude of the magnetic field at the point P is given by N12μ0aJ, then the value of N is
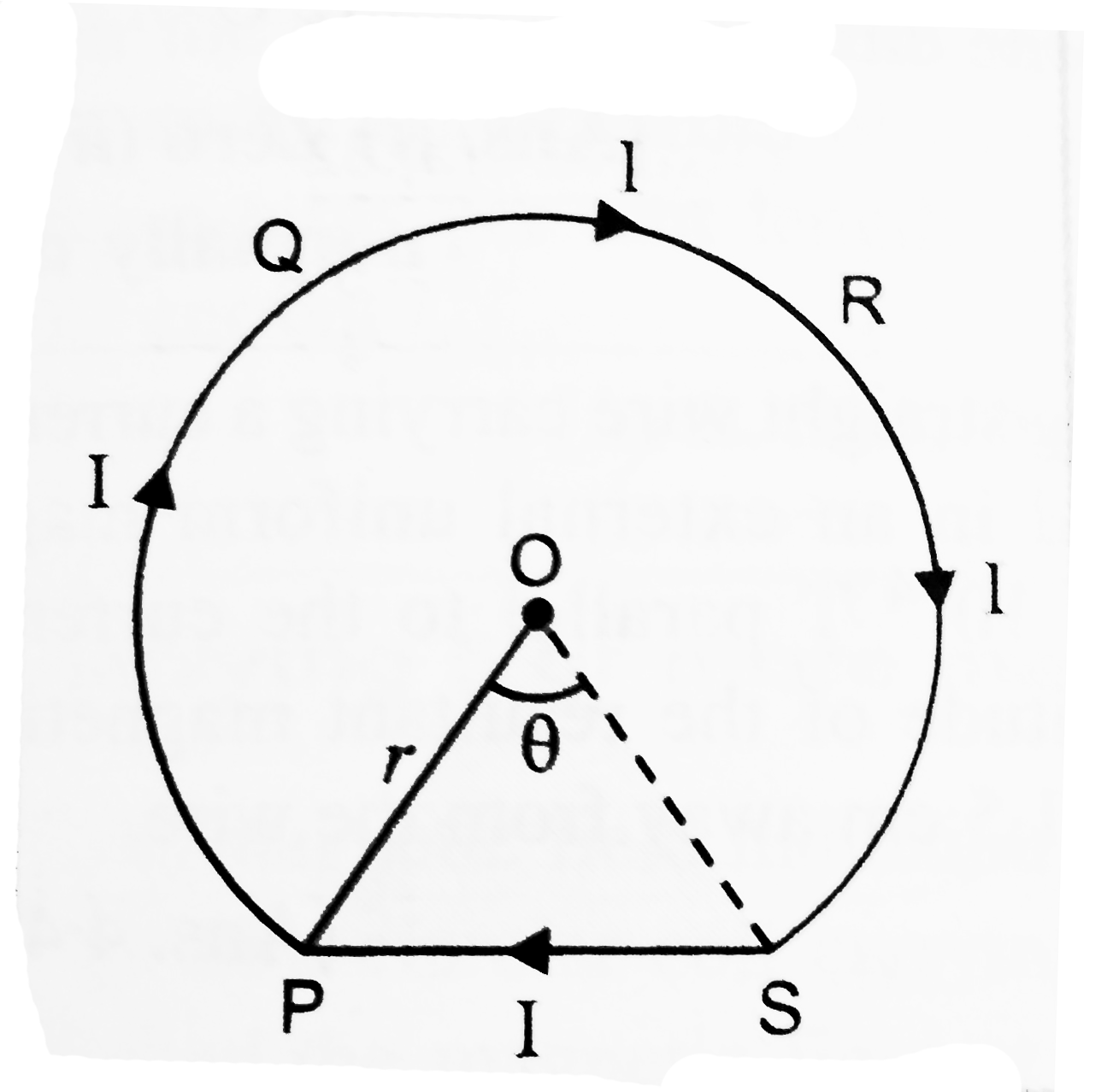
View SolutionA current I(=4A) flows along a thin wire PQRS shaped as shown in figure. The radius of the curved part of the wire is 10⋅0cm. The angle θ=90∘. Find the magnitude of the total magnetic field at the point O.
View Solution
Knowledge Check
A hollow cylinder having infinite length and carrying unifrom current per unit length λ along the circumference as shown Magnetic field inside the cylinder is
 .Aμ0λ2Bμ0λC2μ0λDnone
.Aμ0λ2Bμ0λC2μ0λDnone
An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius R2 are shown in the figure. The remaining portion has uniform volume charge density ρ. The magnitude of electrical field at the centre of the cavity is-AρR6ε0BρR4ε0CρR2ε0DρR3ε0The figure shows the cross-section of a long conducting cylinder of inner radius a and outer radius b. The cylinder carries a current whose current density J=Cr2 where C is a constant. What is the magnitude of the magnetic field B at a point r, where a<r<b?
 AB=μ0πC4πr2(r2−a2)BB=μ0πC4πr2(r4−a4)CB=μ0πC4π(r2−a2)DB=μ0πC4π(r4−a4)
AB=μ0πC4πr2(r2−a2)BB=μ0πC4πr2(r4−a4)CB=μ0πC4π(r2−a2)DB=μ0πC4π(r4−a4)
A thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
View SolutionA cylinder of radius R1 have cylinderical cavity of radius R2 as shown in the figure and have current density J (down ward). Find Magnetic field when
when point is in cavity
View SolutionTwo infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is

View SolutionAn infinitely long hollow conducting cylinder with inner radius r2 and outer radius R carries a uniform current ra density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
View SolutionAn infinitely long hollow conducting cylinder with inner radius R2 and outer radius R carries a uniform current ra density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
View Solution
