Complete Solutions to EXAMPLE of chapter நேர்மாறு முக்கோணவியல் சார்புகள் of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | நேர்மாறு முக்கோணவியல் சார்புகள் |
| SURA PUBLICATION(TAMIL) | EXAMPLE |
| Number Of Questions | 86 |
| Academic Year | 2023-24 |
`sin^-1(cosx), 0lexlepi`-ன் மதிப்பு
01:45View SolutionIf `sin^(-1)x+sin^(-1)y=(2pi)/(3)",then"cos^(-1)x+cos^(-1)y` is equal to
02:03View Solution`sin^-1frac{3}{5}-cos^-1frac{12}{13}+sec^-1frac{5}{3}-cosec^-1frac{13}{12}` என்பதன் மதிப்பு
02:01View Solution`sin^-1x=2sin^-1alpha`-க்கு ஒரு தீர்வு இருந்தால், பின்னர்
02:30View Solution`sin^(-1)(cosx)=(pi)/(2)-x` is valid for
02:40View Solution`sin^-1x+sin^-1y+sin^-1z=frac{3pi}{2}` எனில் `x^100+y^100+z^100-frac{9}{x^101+y^101+z^101}`-ன் மதிப்பு
02:31View Solutionசில `x in R`-க்கு `cot^-1x=frac{2pi}{5}` எனில் `tan^-1x`-ன் மதிப்பு
01:58View Solution`f(x)=sin^-1sqrtx-1` என வரையறுக்கப்படும் சார்பின் சார்பகம்
01:36View Solution`x=1/5` எனில், `cos(cos^-1x+2sin^-1x)`-ன் மதிப்பு
01:58View Solution`tan^-1(1/4)+tan^-1(2/9)` என்பதின் சமம்.
04:39View Solutionசார்பு `f(x)=sin^-1x(x^2-3)x` இருக்கும் இடைவெளி
02:09View Solution`cot^-1 2` மற்றும் `cot^-1 3` ஆகியன ஒரு முக்கோணத்தின் இரு கோணங்கள் எனில், மூன்றாவது கோணமானது
03:03View Solution``sin^-1[tan pi/4]-sin^-1[sqrt3/x]=pi/6`-ல் x என்பதை மூலமாக கொண்ட சமன்பாடு
02:48View Solution`sin^-1(2cos^2x-1)+cos^-1(1-2sin^2x)` =
03:10View Solution`cot^-1(sqrtcosalpha)-tan^-1(sqrtcosalpha)=u` எனில், sinu`-ன் மதிப்பு?
View Solution`|x|le1>` எனில், `2tan^-1x+sin^-1frac{2x}{1+x^2}` என்பதற்கு சமம்.
03:20View Solution`tan^-1x-cot^-1x=tan^-1(1/sqrt3)` என்ற சமன்பாட்டிற்கு
01:52View Solution`sin^-1x+cot^-1(1/2)=pi/2` எனில், x-ன் மதிப்பு
02:52View Solution`sin^-1frac{x}{5}+cosec^-1frac{5}{4}=pi/2` எனில், x-ன் மதிப்பு
04:12View Solution`|x|<1` எனில், `sin(tan^-1x)`-ன் மதிப்பு
01:56View SolutionIf `tan^(-1)((sqrt(1+x^(2))-sqrt(1-x^(2)))/(sqrt(1+x^(2))+sqrt(1-x^(2))))=alpha" then prove that "x^(2)=sin2alpha.`
06:10View SolutionShow that `sin^-1 x+cos^-1 x=pi/2`.
02:01View Solution`tan^-1 2x+tan^-1 3x=pi/4` என்ற சமன்பாட்டிற்கான தீர்வுகளின் எண்ணிக்கை
03:38View Solution`alpha=tan^-1(tanfrac{5pi}{4})` மற்றும் `beta=tan^-1(-tanfrac{2pi}{3})` எனில்,
03:34View Solution`sqrt(1+cos2x)=sqrt2sin^-1(sinx),-piltxltpi` என்ற சமன்பாட்டின் மெய் தீர்வுகளின் எண்ணிக்கை
04:18View Solution`alpha=tan^-1(frac{sqrt3x}{2y-x}), beta=tan^-1(frac{2x-y}{sqrt3y})` எனில் `alpha-beta`=
04:54View Solution`tan^-1(1/4)+tan^-1(2/11)`=
02:05View Solution`tan^-1(3)+tan^-1(x)=tan^-1(8) எனில், x=?
02:13View Solution`cos^-1(frac{cos5pi}{3})+sin^-1(frac{sin5pi}{3})`-இன் மதிப்பு
02:42View Solution`sin{2cos^(-1)((-3)/(5))}=`
02:41View Solution`4cos^-1x+sin^-1x=pi` எனில் x =
02:29View SolutionIf `tan^(-1)((x+1)/(x-1))+tan^(-1)((x-1)/(x))=tan^(-1)(-7),` then x is
04:34View Solution`cos^-1x>sin^-1x` எனில்,
03:17View Solution`int_-4^4[tan^-1(frac{x^2}{x^4+1})+tan^-1(frac{x^4+1}{x^2})]dx` இன் மதிப்பு
03:47View Solution`cot((pi)/(4)-2cot^(-1)3)`
04:24View Solution`tan^-1(cottheta)=2theta` எனில், `theta` =
01:49View Solution`cos^-1(x^2-4)` சார்பகமானது
03:24View Solution`tan(cos^-1frac{3}{5}+tan^-1frac{1}{4})` இன் மதிப்பு
View SolutionThe value of `sin(2(tan^(-1)0.75)` is ………..
02:18View SolutionIf `xgt1,"then"2tan^(-1)x+sin^(-1)((2x)/(1+x^(2)))` is……………
01:19View Solution`theta=sin^-1(sin(-60^@)) `எனில் `theta`-விற்கு சாத்தியமான ஒரு மதிப்பு
02:42View Solution`sin^-1(cosfrac{33pi}{5})` இன் மதிப்பு
View Solutionx<0, y<0 என்றவாறு xy = 1, எனில் `tan^-1(x)+tan^-1(y)`=
View Solution`sin^-1(frac{-1}{2})` -ன் முதன்மை மதிப்பு
01:43View Solution`tan^-1(tanfrac{9pi}{8})`
02:26View Solutionபொருந்தாத ஒன்றைத் தோ்ந்தெடுக்க. சைன் நேர்மாறு சார்புக்கு
02:07View Solutionபொருந்தாத ஒன்றைத் தோ்ந்தெடுக்க. கொசைன் நேர்மாறு சார்புக்கு
02:15View Solutionபொருந்தாத ஒன்றைத் தோ்ந்தெடுக்க. நேர்மாறு தொடுகோட்டுச் சார்புக்கு
02:24View Solutionபொருந்தாத ஒன்றைத் தோ்ந்தெடுக்க.
03:24View Solutionபொருந்தாத ஒன்றைத் தோ்ந்தெடுக்க.
04:01View Solutionதவறான விடையை தேர்ந்தெடுக்க.
03:15View Solutionதவறான விடையை தேர்ந்தெடுக்க.
02:34View Solutionதவறான விடையை தேர்ந்தெடுக்க.
02:48View Solutionதவறான விடையை தேர்ந்தெடுக்க.
02:43View Solutionதவறான விடையை தேர்ந்தெடுக்க.
02:41View Solutionபொருத்துக.
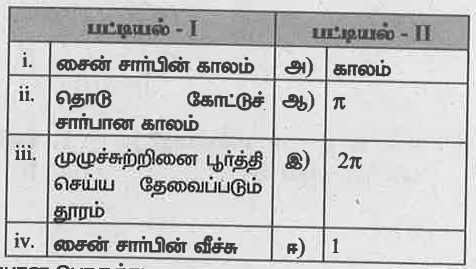 02:36View Solution
02:36View Solutionபொருத்துக.
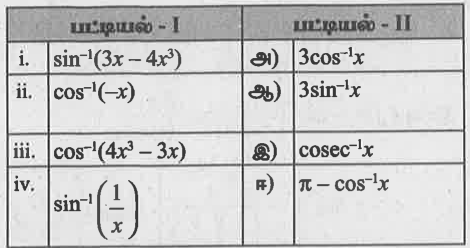 04:35View Solution
04:35View Solutionபொருத்துக.
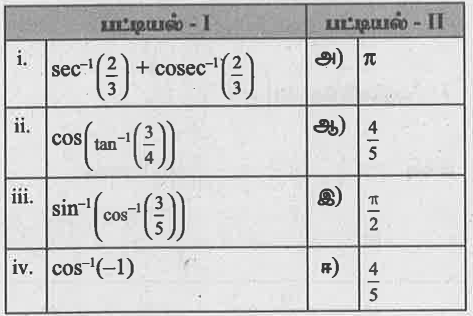 04:32View Solution
04:32View Solutionபொருத்துக.
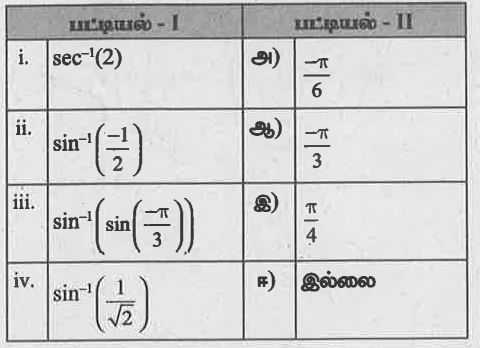 04:51View Solution
04:51View Solutionபொருத்துக.
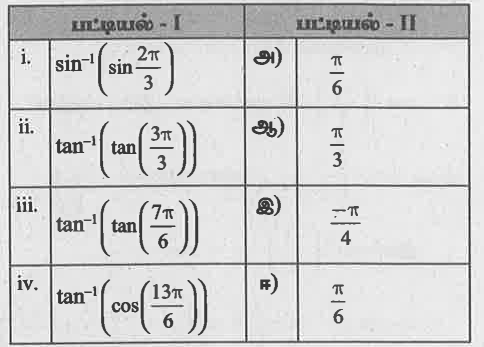 07:02View Solution
07:02View Solution`tan^-1(frac{-1}{sqrt3})` முதன்மை மதிப்பு காண்க
01:57View Solution`sin^-1(-1)`- ன் முதன்மை மதிப்பு காண்க
02:17View Solution`cos^-1(frac{-1}{2})`- ன் முதன்மை மதிப்பு காண்க
03:15View Solution`cot^-1(frac{1}{7})=theta`, எனில் `cos theta`-ன் மதிப்பு காண்க.
02:19View Solution`sin^-1(1/2)=tan^-1x` எனில், x-ன் மதிப்பு காண்க.
02:35View Solutionநிரூபிக்க : `tan^-1(1/7)+tan^-1(1/13)=tan^-1(2/9)`
03:38View Solutionமதிப்பிடுக.`sin(cos^-1(3/5))`
02:43View Solutionமதிப்பிடுக. `sin(1/2cos^-1 frac{4}{5})`
03:46View Solutionநிரூபிக்க : `2tan^-1(2/3)=tan^-1(12/5)`
02:58View Solutionமதிப்பிடுக. `sin(cos^-1(1/2))`
02:25View SolutionProve that `cos^(-1)((4)/(5))+tan^(-1)((3)/(5))=tan^(-1)((27)/(11))`
03:44View Solutionமதிப்பிடுக. `cos[sin^-1frac{3}{5}+sin^-1 frac{5}{13}]`
04:38View SolutionProve that `tan^(-1)((m)/(n))-tan^(-1)((m-n)/(m+n))=(pi)/(4).`
02:42View Solutionதீர்க்க. `tan^-1(frac{x-1}{x-2})+tan^-1(frac{x+1}{x+2})=pi/4`
07:41View SolutionSolve : `tan^(-1)((2x)/(1-x^(2)))+cot^(-1)((1-x^(2))/(2x))=(pi)/(3),xgt0`
03:02View Solution`sin(sin^-1 frac{1}{5}+cos^-1x)=1` எனில் x-ன் மதிப்பு காண்க
02:14View SolutionProve that `tan^(-1)sqrt(x)=(1)/(2)cos^(-1)((1-x)/(1+x)),x""in[0,1]`
01:44View Solutionமதிப்பிடுக : `int_-1^1log(frac{2-x}{2+x})dx`
02:39View Solutionசமன்பாட்டின் மெய் தீர்வுகள் காண்க. ``tan^-1sqrtx(x+1)+sin^-1sqrtx^2+x+1=pi/2`
03:07View SolutionSolve : `cos(tan^(-1)x)=sin(cot^(-1)""(3)/(4))`
06:05View Solutionபின்வரும் சார்புகளில் சார்பகம் காண்க. `f(x)=sin^-1(2x - 3)`
01:43View Solutionபின்வரும் சார்புகளில் சார்பகம் காண்க. `f(x)=sin^-1x+cos x`
01:54View SolutionWrite the function `f(x)=tan^(-1)sqrt((a-x)/(a+x))-altxlta` in the simplest form.
02:36View Solutionசுருக்குக. `sin^-1(frac{sinx+cosx}{sqrt2}),frac{-pi}{4}ltxltpi/4`
02:19View Solution`tan^-1(frac{sqrt(1+x^2)-sqrt(1-x^2)}{sqrt(1+x^2)+sqrt(1-x^2)})=alpha` எனில் `x^2=sin2 alpha` என நிரூபிக்க.
06:31View SolutionProve that `tan^(-1)((1-x)/(1+x))-tan^(-1)((1-y)/(1+y))=sin^(-1)((y-x)/(sqrt(1+x^(2))*sqrt(1+y^(2))))`
07:57View Solution
EXAMPLE questions and complete solutions for chapter நேர்மாறு முக்கோணவியல் சார்புகள் of SURA MATHS (TAMIL) of Class 12
