Complete Solutions to Exercise of chapter LINES AND ANGLES of Class 7 book with complete answers and questions
| Class 7 | MATHS |
| Chapter | LINES AND ANGLES |
| NCERT EXEMPLAR | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The angles between North and West and South and East are
View SolutionAngles between South and West and South and East are
View SolutionIn Fig. 5.9, PQ is a mirror, AB is the incident ray and BC is the reflected ray. If `angleABC = 46^(@)`, then `angleABP` is equal to
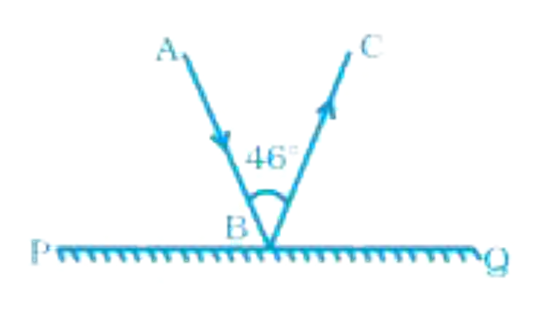
View SolutionIf the complement of an angle is `79^(@)`, then the angle will be of
View SolutionAngles which are both supplementary and vertically opposite are
View SolutionThe angle which makes a linear pair with an angle of `61^(@)` is of
View SolutionThe angles x and `90^(@) - x` are
View SolutionThe angles x – `10^(@)` and `190^(@)` – x are
View SolutionIn Fig. 5.10, the value of x is
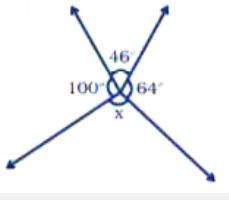
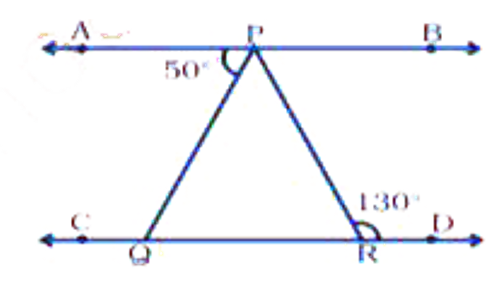
View SolutionIn Fig. 5.11 , if AB || CD , `angleAPQ = 50^(@)` and `anglePRD = 130^(@)` , then `angleQPR` is
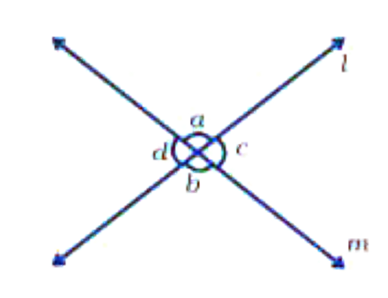
View SolutionIn Fig. 5.12, lines l and m intersect each other at a point. Which of the following is false?
View SolutionIf angle P and angle Q are supplementary and the measure of angle P is `60^(@)` , then the measure of angle Q is
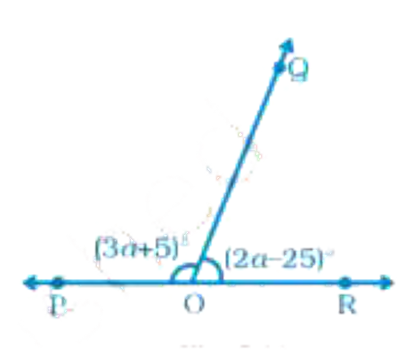
View SolutionIn Fig. , POR is a line . The value of a is
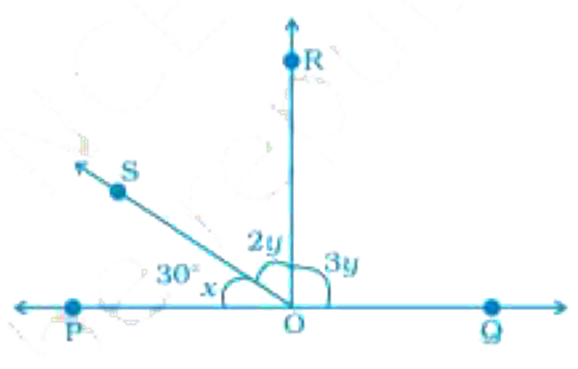
View SolutionIn Fig. 5.14 . POQ is a line . If x = `30^(@)` , then `angleQOR` is
View SolutionThe measure of an angle which is four times its supplement is
View SolutionIn Fig. 5.15, the value of y is

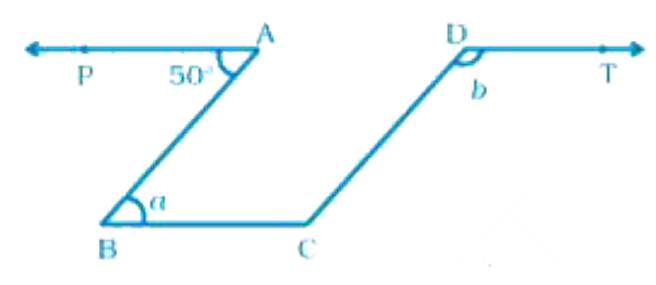
View SolutionIn Fig. 5.16, PA || BC || DT and AB || DC. Then, the values of a and b are respectively.
View SolutionThe difference of two complementary angles is `30^(@)` . Then, the angles are
View SolutionIn Fig. PQ || SR and SP || RQ. Then, angles a and b are respectively
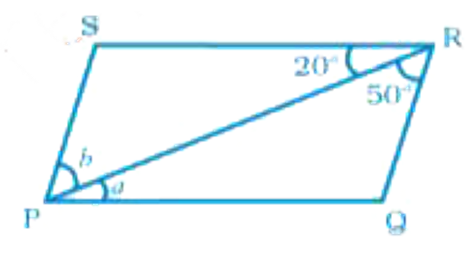
View SolutionIn Fig a and b are
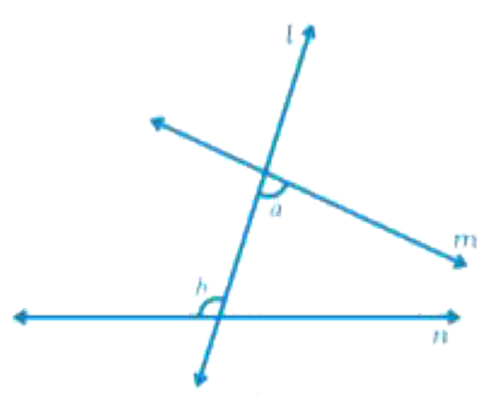
View SolutionIf two supplementary angles are in the ratio `1 : 2`, then the bigger angle is
View SolutionIn Fig. 5.19, `angleROS` is a right angle and `anglePOR` and `angleQOS` are in the ratio 1 : 5. Then, `angleQOS` measures
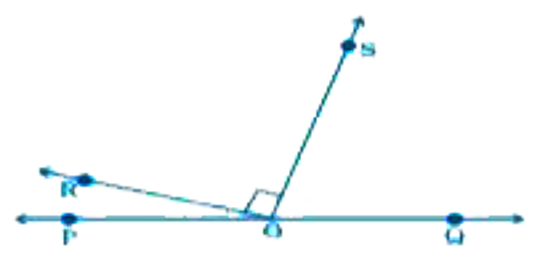
View SolutionStatements a and b are as given below:
a : If two lines intersect, then the vertically opposite angles are equal.
b : If a transversal intersects, two other lines, then the sum of two interior angles on the same side of the transversal is `180^(@)`.
Then
View SolutionFor Fig. 5.20, statements p and q are given below:
p : a and b are forming a linear pair.
q : a and b are forming a pair of adjacent angles.
Then
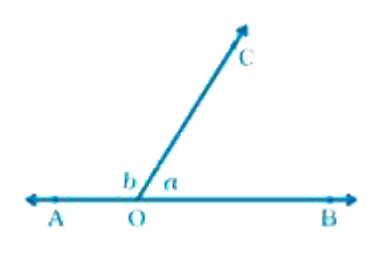
View SolutionIn Fig. 5.21, `angleAOC` and `angleBOC` form a pair of

View SolutionIn Fig. 5.22, the value of a is

View SolutionIn Fig. 5.23, if QP || SR, the value of a is
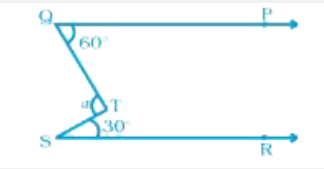
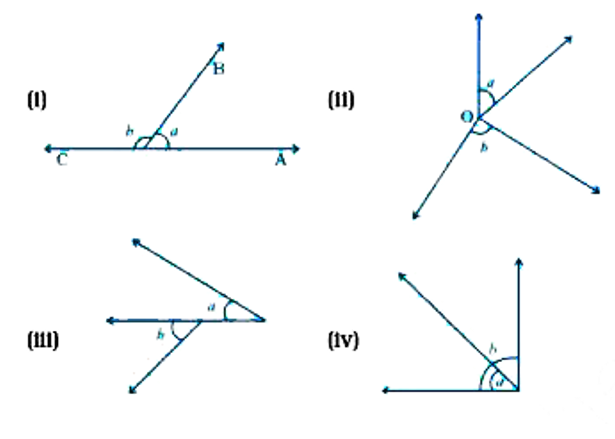
View SolutionIn which of the following figures, a and b are forming a pair of adjacent angles?
View SolutionIn a pair of adjacent angles, (i) vertex is always common, (ii) one arm is always common, and (iii) uncommon arms are always opposite rays
Then
View SolutionIn Fig. 5.25, lines PQ and ST intersect at O. If `anglePOR = 90^(@)` and x : y = 3 : 2, then z is equal to
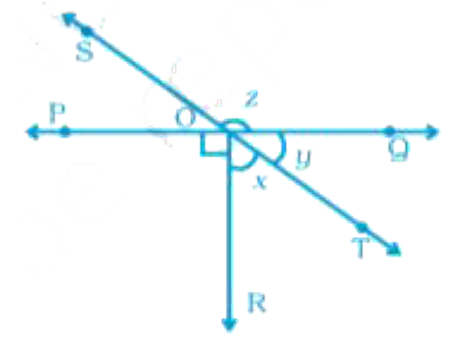
View SolutionIn Fig. 5.26, POQ is a line, then a is equal to
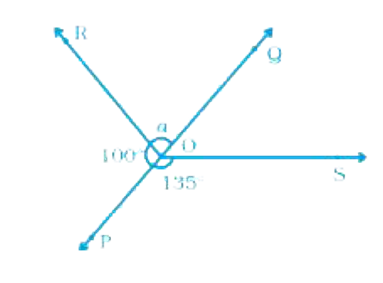
View SolutionVertically opposite angles are always
View SolutionIn Fig. 5.27, a = `40^(@)` . The value of b is
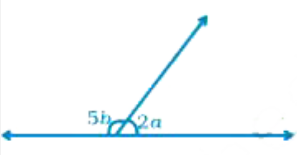
View SolutionIf an angle is `60^(@)` less than two times of its supplement, then the greater angle is
View SolutionIn Fig. 5.28, PQ || RS. If `angle1=(2a+b)^(@)` and `angle6=(3a–b)^(@)`, then the measure of `angle2` in terms of b is
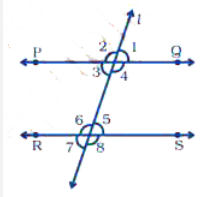
View SolutionIn Fig. 5.29, PQ||RS and `a : b = 3 : 2`. Then, f is equal to

View SolutionIn Fig. 5.30, line l intersects two parallel lines PQ and RS. Then, which one of the following is not true?
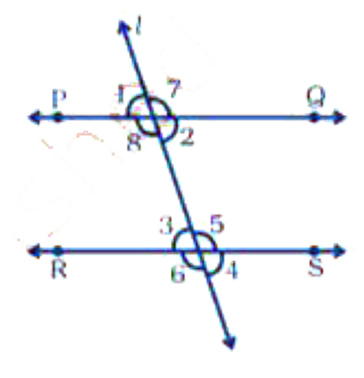
View SolutionIn Fig. 5.30, which one of the following is not true?
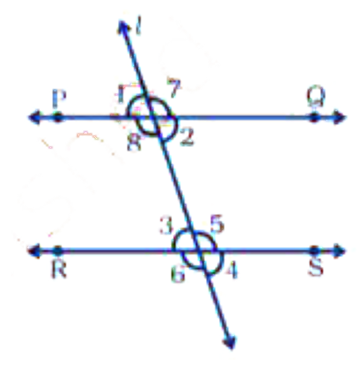
View SolutionIn Fig. 5.30, which of the following is true?

View SolutionIn Fig. 5.31, PQ||ST. Then, the value of x + y is
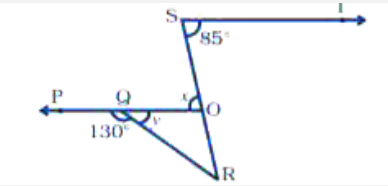
View SolutionIn Fig. 5.32, if PQ||RS and QR||TS, then the value a is

View SolutionIf a transversal intersects two parallel lines, then
sum of interior angles on the same side of a transversal is _______
View SolutionIf a transversal intersects two parallel lines, then
alternate interior angles have one common _______
View SolutionIf a transversal intersects two parallel lines, then
corresponding angles are on the ______ side of the transversal
View SolutionIf a transversal intersects two parallel lines, then
alternate interior angles are on the _______ side of the transversal.
View SolutionTwo lines in a plane which do not meet at a point anywhere are _______ called lines.
View SolutionTwo angles forming a __________ pair are supplementary.
View SolutionThe supplement of an acute is always __________ angle.
View SolutionThe supplement of a right angle is always _________ angle.
View SolutionThe supplement of an obtuse angle is always _________ angle.
View SolutionIn a pair of complementary angles, each angle cannot be more than ________ .
View SolutionAn angle is `45^(@)`. Its complementary angle will be __________ .
View SolutionAn angle which is half of its supplement is of __________.
View SolutionState whether the statements are True or False.
Two right angles are complementary to each other.
View SolutionState whether the statements are True or False.
One obtuse angle and one acute angle can make a pair of complementary angles.
View SolutionState whether the statements are True or False.
Two supplementary angles are always obtuse angles.
View SolutionState whether the statements are True or False.
Two right angles are always supplementary to each other.
View SolutionState whether the statements are True or False.
One obtuse angle and one acute angle can make a pair of suplementary angles.
View SolutionState whether the statements are True or False.
Both angles of a pair of supplementary angles can never be acute angles.
View SolutionState whether the statements are True or False.
Two supplementary angles always form a linear pair.
View SolutionState whether the statements are True or False.
Two angles making a linear pair are always supplementary.
View SolutionState whether the statements are True or False.
Two angles making a linear pair are always adjacent angles.
View SolutionState whether the statements are True or False.
Vertically opposite angles form a linear pair.
View SolutionState whether the statements are True or False.
Interior angles on the same side of a transversal with two distinct parallel lines are complementary angles.
View SolutionState whether the statements are True or False.
Vertically opposite angles are either both acute angles or both obtuse angles.
View SolutionState whether the statements are True or False.
A linear pair may have two acute angles.
View SolutionState whether the statements are True or False.
An angle is more than `45^(@)`. Its complementary angle must be less than `45^(@)` .
View SolutionState whether the statements are True or False.
Two adjacent angles always form a linear pair.
View SolutionWrite down each pair of adjacent angles shown in the following figures:

View SolutionIn each of the following figures, write, if any, (i) each pair of vertically opposite angles, and (ii) each linear pair.
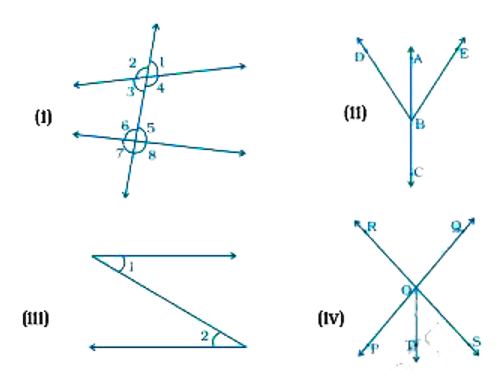
View SolutionName the pairs of supplementary angles in the following figures:
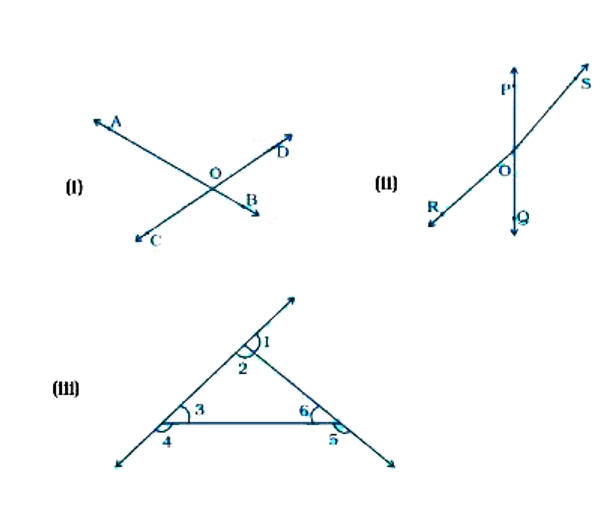
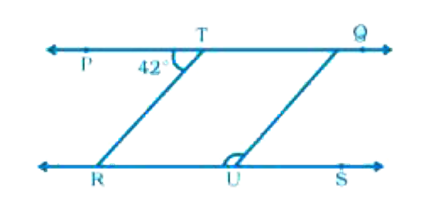
View SolutionIn Fig. 5.36, PQ || RS, TR || QU and `anglePTR = 42^(@)`. Find `angleQUR`.
View SolutionThe drawings below (Fig. 5.37), show angles formed by the goalposts at different positions of a football player. The greater the angle, the better chance the player has of scoring a goal. For example, the player has a better chance of scoring a goal from Position A than from Position B.
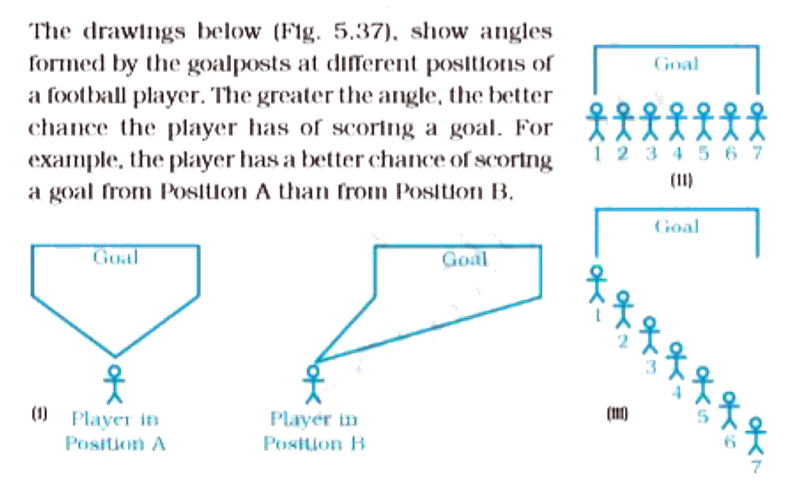
In Parts (a) and (b) given below it may help to trace the diagrams and draw and measure angles.
(a) Seven football players are practicing their kicks. They are lined up in a straight line in front of the goalpost [Fig.(ii)]. Which player has the best (the greatest) kicking angle?
(b) Now the players are lined up as shown in Fig. (iii). Which player has the best kicking angle?
(c) Estimate atleast two situations such that the angles formed by different positions of two players are complement to each other.
View SolutionThe sum of two vertically opposite angles is `166^(@)`. Find each of the angles.
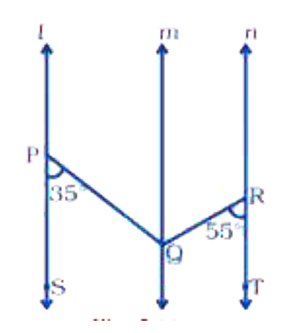
View SolutionIn Fig. 5.38, l ||m||n. `angleQPS = 35^(@)` and `angleQRT = 55^(@)`. Find `anglePQR`.
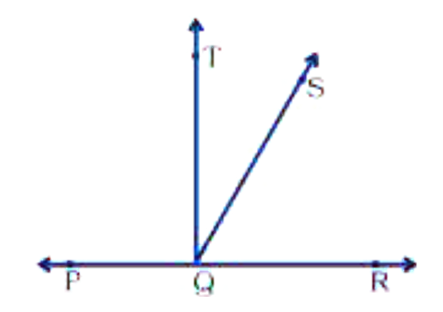
View SolutionIn Fig. 5.39, P, Q and R are collinear points and TQ `bot` PR,
Name, (a) pair of complementary angles
(b) two pairs of supplementary angles.
(c) four pairs of adjacent angles.
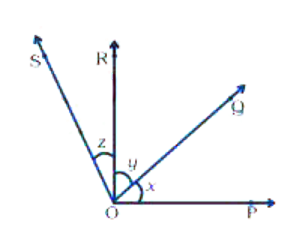
View SolutionIn Fig. 5.40, OR `bot` OP.
(i) Name all the pairs of adjacent angles.
(ii) Name all the pairs of complementary angles.
View SolutionIn (Fig 5.42) are the following pairs of angles adjacent? Justify your answer.
View SolutionIn Fig. 5.43, write all the pairs of supplementary angles.
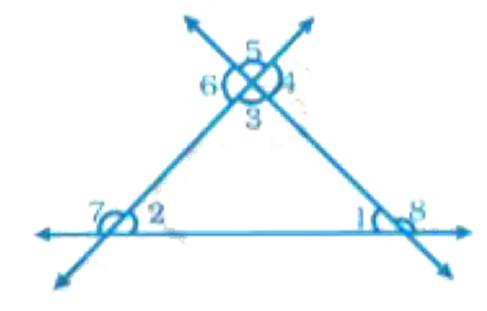
View SolutionWhat is the type of other angle of a linear pair if
(a) one of its angle is acute?
(b) one of its angles is obtuse?
(c) one of its angles is right?
View SolutionCan two acute angles form a pair of supplementary angles? Give reason in support of your answer.
View SolutionTwo lines AB and CD intersect at O (Fig. 5.44). Write all the pairs of adjacent angles by taking angles 1, 2, 3, and 4 only.
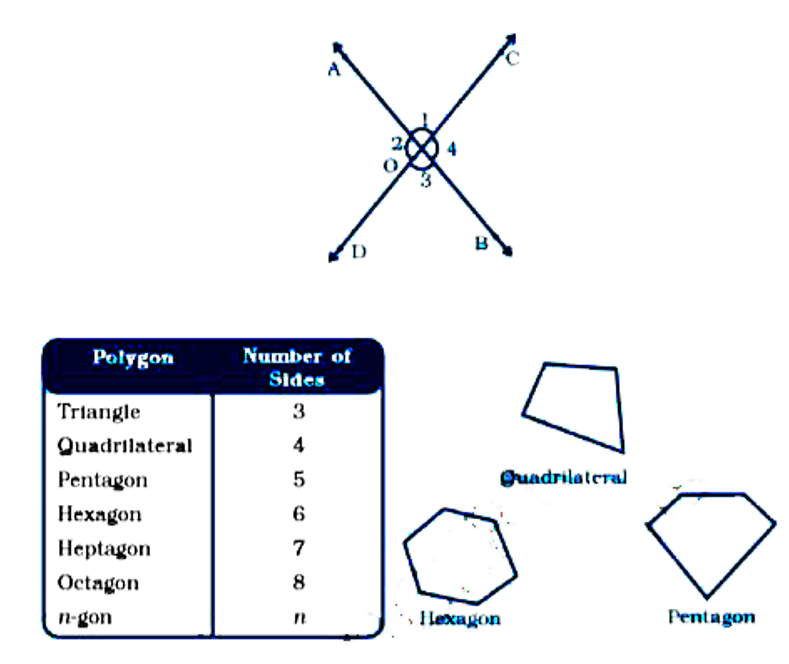
View SolutionIf the complement of an angle is 62°, then find its supplement.
View SolutionA road crosses a railway line at an angle of 30° as shown in Fig.5.45. Find the values of a, b and c.
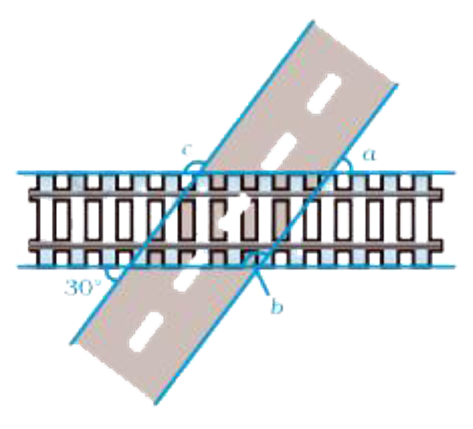
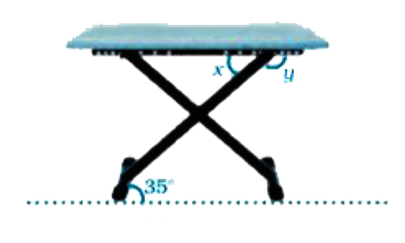
View SolutionThe legs of a stool make an angle of `35^(@)` with the floor as shown in Fig. 5.46. Find the angles x and y.
View SolutionIron rods a, b, c, d, e and f are making a design in a bridge as shown in Fig. 5.47, in which a ||b, c ||d, e || f. Find the marked angles between
(i) b and c
(ii) d and e
(iii) d and f
(iv) c and f
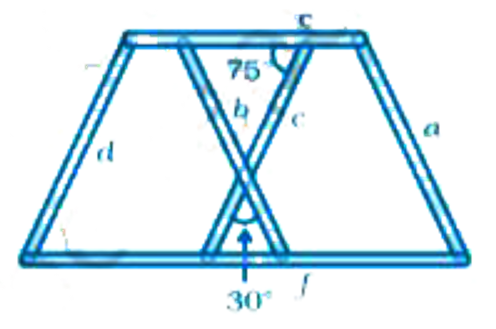
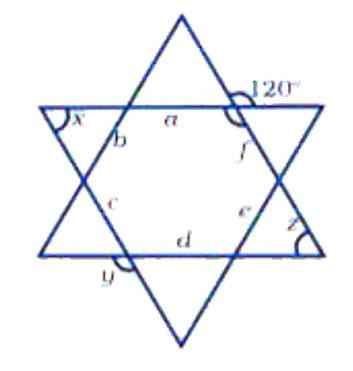
View SolutionAmisha makes a star with the help of line segments a, b, c, d, e and f, in which a || d, b || e and c || f. Chhaya marks an angle as `120^(@)` as shown in Fig. 5.48 and asks Amisha to find the `anglex, angley` and `anglez`. Help Amisha in finding the angles.
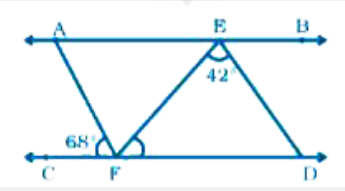
View SolutionIn Fig. 5.49, AB||CD, AF||ED, `angleAFC = 68^(@)` and `angleFED = 42^(@)`. Find `angleEFD`.
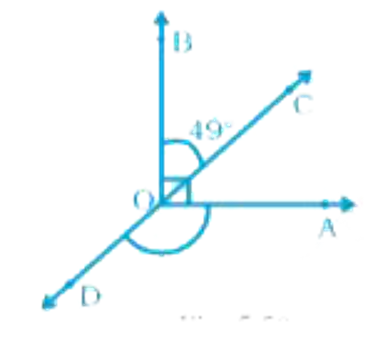
View SolutionIn Fig. 5.50, OB is perpendicular to OA and `angleBOC = 49^(@)`. Find `angleAOD.`
View SolutionThree lines AB, CD and EF intersect each other at O. If `angleAOE` = `30^(@)` and `angleDOB = 40^(@)` (Fig. 5.51), find COF.

View SolutionMeasures (in degrees) of two complementary angles are two consecutive even integers. Find the angles.
View SolutionTwo angles are making a linear pair. If one of them is one-third of the other, find the angles.
View SolutionMeasures (in degrees) of two supplementary angles are consecutive odd integers. Find the angles.
View SolutionIn Fig. 5.53, find the value of BOC, if points A, O and B are collinear.
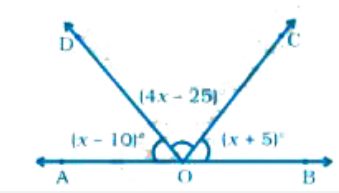
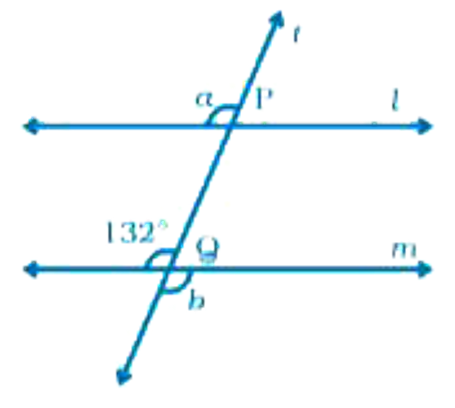
View SolutionIn Fig. 5.55, l ||m and a line t intersects these lines at P and Q, respectively. Find the sum 2a + b.
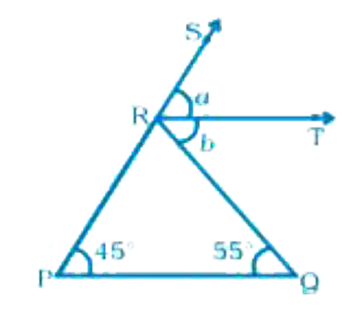
View SolutionIn Fig. 5.56, QP || RS. Find the values of a and b.

View SolutionIn Fig. 5.57, PQ || RT. Find the value of a + b.
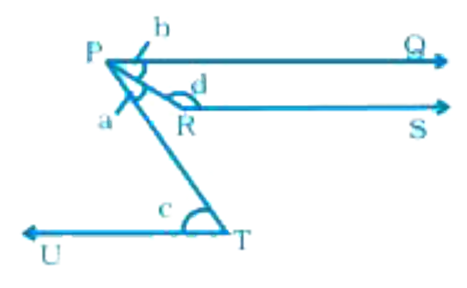
View SolutionIn Figure, `PQ, RS` and `UT` are parallel lines.
(i) If `c =` `57^(@)` and `a = (c)/(3)` , find the value of `d` .
(ii) If `c =` `75^(@)` and `a = (2)/(5)` `c` , find `b`.
View SolutionIn Fig. 5.59, AB||CD . Find the reflex `angleEFG`.

View SolutionIn Fig. 5.60, two parallel lines l and m are cut by two transversals n and p. Find the values of x and y.
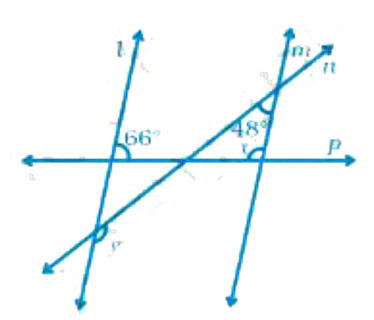
View Solution
Exercise questions and complete solutions for chapter LINES AND ANGLES of NCERT EXEMPLAR of Class 7