Complete Solutions to EXERCISE of chapter SPECIAL TYPES OF QUADRILATERALS of Class 8 book with complete answers and questions
| Class 8 | MATHS |
| Chapter | SPECIAL TYPES OF QUADRILATERALS |
| SELINA PUBLICATION | EXERCISE |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
In parallelogram ABCD, `angleA=3cm` times `angleB`. Find all the angles of the parallelogram. In the same parallelogram, if AB=5x-7 and CD=3x+1, find the length of CD.
View SolutionIn parallelogram PQRS, `angleQ=(4x-5)^(@) and angleS=(3x+10)^(@)`. Calculate: `angleQ and angleR`.
View SolutionIn rhombus ABCD:
(i) if `angleA=74^(@)`, find `angleB and angleC`.
(ii) if `AD=7*5cm`, find BC and CD.
View SolutionIn square PQRS:
(i) if `PQ=3x-7 and QR=x+3`, find PS.
(ii) if PR=5x and QS=9x-8. find QS.
View Solution
ABCD is a rectangle.
If `angleBPC=124^(@)`.
Calculate:
(i) `angleBAP`
(ii) `angleADP`.
View Solution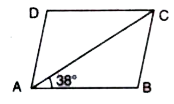
ABCD is a rhombus. If `angleBAC=38^(@),` find:
(i) `angleACB`
(ii) `angleDAC`
(iii) `angleADC`.
View SolutionABCD is a rhombus. If `angleBCA=35^(@), and angleADC`.
View SolutionPQRS is a parallelogram whose diagonals intersect at M.
if `anglePMS=54^(@),angleQSR=25^(@) and angleSQR=30^(@)`, find:
(i) `angleRPS`
(ii) `anglePRS`
(iii) `anglePSR`.
View Solution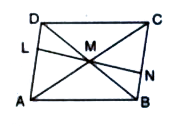 .
.
Given: Parallelogram
ABCD in which diagonals AC and CD intersect at M.
Prove: M is mid-point of LN.
View SolutionIn an isosceles-trapezium, show that the opposite angles are supplementary.
View SolutionABCD is a parallelogram. What kind of quadrilateral is it if:
(i) AC=CD and AC is perpendicular to BD?
(ii) AC is perpendicular to BD but is not equal to it ?
(iii) AC=BD but AC is not perpendicular to BD ?
View SolutionProve that the diagonals of a parallelogram bisect each other.
View SolutionIf the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
View SolutionIn parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
View SolutionIn parallelogram ABCD, E is the mid-point of side AB and CE bisect angle BCD. Prove that :
(i) AE=AD
(ii) DE bisect `angleADC` and
(iii) Angle DEC is a right angle.
View Solution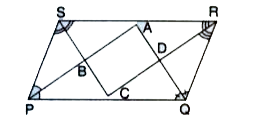
In the alongside diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
Show that:
(i) `anglePSB+angleSPB=90^(@)`
(ii) `anglePBS=90^(@)`
(iii) `angleABC=90^(@)`
(iv) `angleADC=90^(@)`
(v) `angleA=90^(@)`
(vi) ABCD is a rectangle
thus, the bisectors of the angles of a parallelogram enclose a rectangle.
View SolutionIn parallelogram ABCD, X and Y are mid-points of opposite sides AB and DC respectively. Prove that:
(i) AX=YC.
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
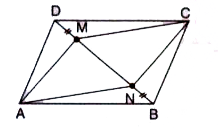
View SolutionThe given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM=BN
 .
.
Prove that:
(i) `DeltaDMCcong DeltaBNA` and so CM=AN.
(ii) `DeltaAMDcongDeltaCNB` and so `AM=CN`.
(iii) ANCM is a parallelogram.
View Solution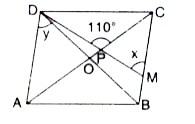 .
.
The given figure shows a rhombus ABCD in which angle `BCD=80^(@)`. Find angles x and y.
View SolutionUse the information given in the following diagram to find the values of x, y and z.
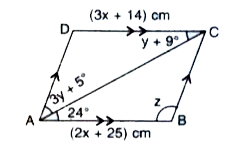 .
.
View SolutionThe following figure is a rectangle in which x:y=3:7, find the values of x and y.
 .
.
View SolutionIn the given figure, `AB////EC,AB=AC and AE` bisects `angleDAC`. Prove that:
(i) `angleEAC=angleACB`
(ii) ABCE is a parallelogram.
 .
.
View Solution
EXERCISE questions and complete solutions for chapter SPECIAL TYPES OF QUADRILATERALS of ICSE of Class 8