Complete Solutions to EXERCISE 5.2 of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| CPC CAMBRIDGE PUBLICATION | EXERCISE 5.2 |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
In an isosceles ABC, with AB = AC, the bisectors of `angleB` and `angleC` intersect each other at O. Joint A to O. Show that:
(ii) OB = OC
(ii) AO bisects `angleA`
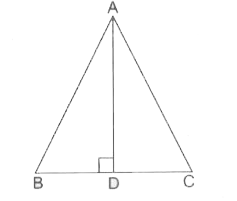
View SolutionIn `triangleABC, AD` is the perpendicular bisector of BC. Show that `triangleABC` is an isosceles triangle in which AB = AC.
View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively. Show that these altitudes are equal.
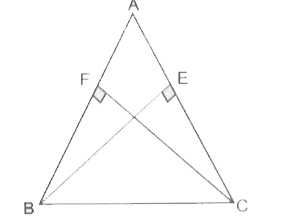
View SolutionABC is a triangle in which altitude BE and CF to sides AC and AB are equal. Show that
`Delta ABE ~= Delta ACF`
(ii) AB = AC, i.e., ABC is an isosceles triangle.

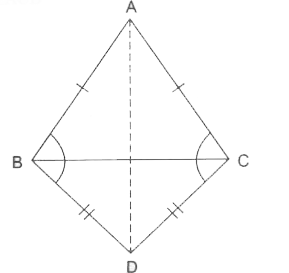
View SolutionABC and DBC are two isosceles triangles on the same base BC. Show that, `triangleABD = angleACD`
View Solution`triangleABC` is an isosceles triangle in which AB= AC. Side BA is produced to D such that AD = AB. Show that `angleBCD` is a right angle.

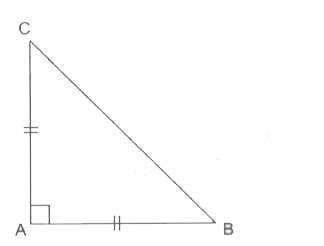
View SolutionABC is a right triangle in which `angleA = 90^(@)` and AB = AC. Find `angleB` and `angleC`.
View SolutionShow tht the angles of an equilateral triangle are `60^(@)` each.
View Solution
EXERCISE 5.2 questions and complete solutions for chapter TRIANGLES of CAMBRIDGE MATHS (KANNADA ENGLISH) of Class 9