ABC is a triangle in which altitude BE and CF to sides AC and AB are equal. Show that
ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
 Solution in Kannada
Solution in Kannada
Step by step video & image solution for ABC is a triangle in which altitude BE and CF to sides AC and AB are equal. Show that Delta ABE ~= Delta ACF (ii) AB = AC, i.e., ABC is an isosceles triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 5.3
5 Videos
- TRIANGLES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 5.4
6 Videos
- TRIANGLES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 5.5 (Optional)
4 Videos
- SURFACE AREAS AND VOLUMES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - EXERSICE 13.8
10 Videos
Similar Questions
△ABC and △DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
(i) △ABD≅△ACD
(ii) △ABP≅△ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.

View SolutionShow that in a right angled triangle, the hypotenuse is the longest side.
View SolutionABC is a triangle . Locate a point in the interior of △ABC which is equidistant from all the vertices of △ABC.
View SolutionFind the volume of a sphere whose radius is
(i) 7 cm,
(ii) 0.63m
View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
View SolutionABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए शीर्षलम्ब BE और CF बराबर है। दर्शाइए कि
(i) ΔABE≅ΔACF
(ii) AB=AC, अर्थात ΔABC एक समद्विबाहु त्रिभुज है।
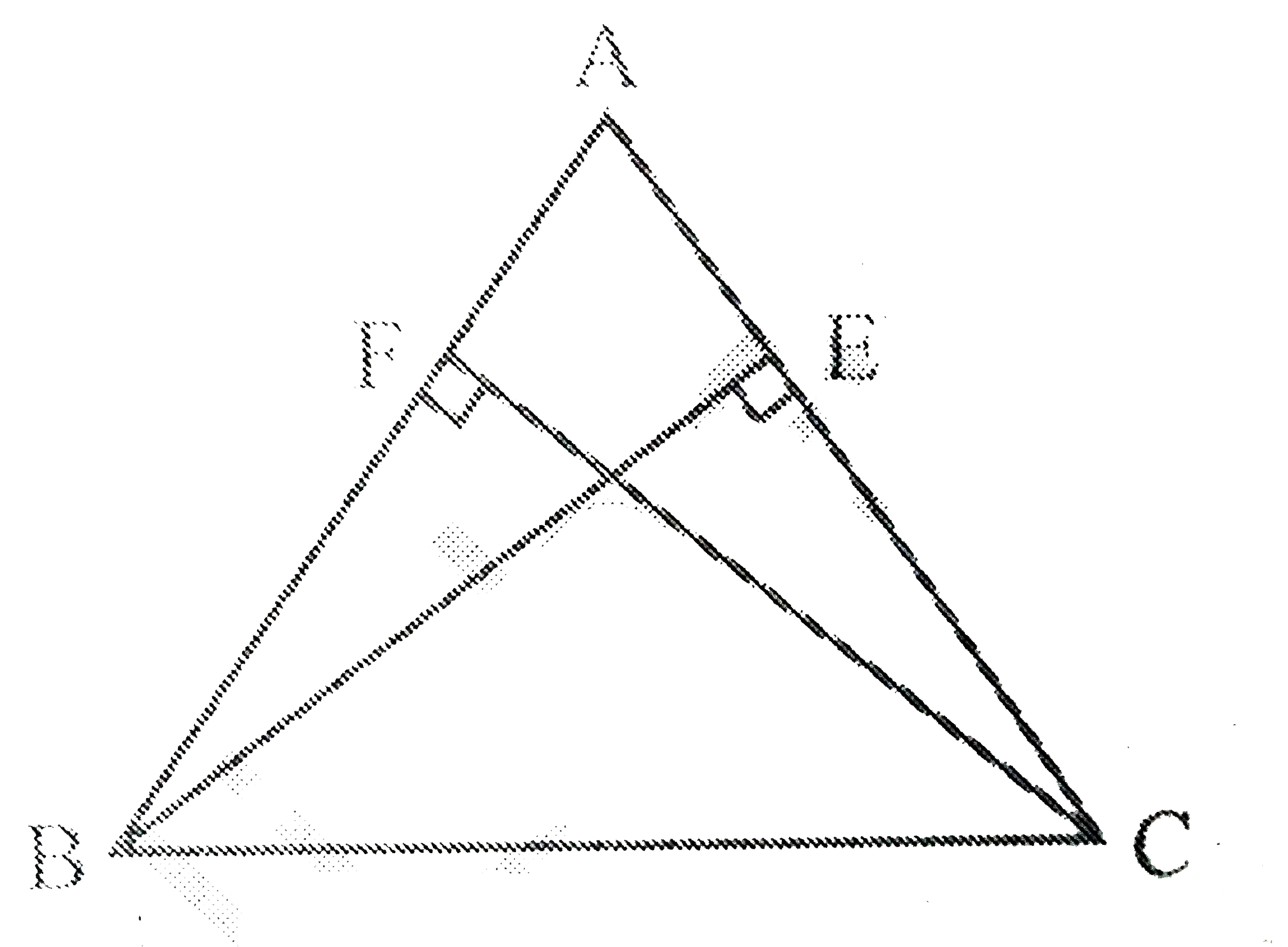
View Solutionएक त्रिभुज ABC है जिसमें ऊँचाइयाँ BE और CF भुजाओं AC और AB के बराबर है तो दिखाइये कि-
(i) ΔABE≅ΔACF
(ii) AB=AC,अर्थात ABC एक समद्विबाहु त्रिभुज है ।

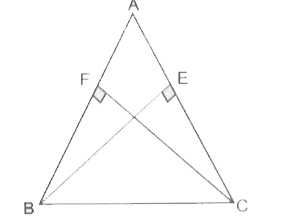
View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively. Show that these altitudes are equal.

View SolutionABC is a triangle in which altitude BE and CF to sides AC and AB are equal. Show that
ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.

View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively. Show that these altitudes are equal.
View SolutionΔABC లో AC,AB భుజాలకు గీసిన లంబాలు BE,CF లు సమానము అయిన AB =AC అనగా ΔABC ఒక సమద్విబహు త్రిభుజామని చూపండి.

View SolutionABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
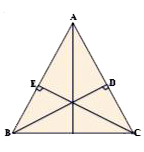
View SolutionABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
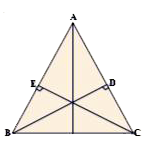
View SolutionABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
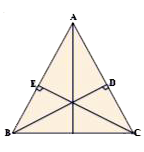
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that ( i ) △ABE≅△ACF
(ii) AB = AC i.e ABC is an isoceles triangle
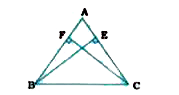
View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively (See Fig.
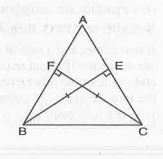 ). Show that these altitudes are equal.
). Show that these altitudes are equal.
View Solution
