Complete Solutions to EXERCISE 5.3 of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| CPC CAMBRIDGE PUBLICATION | EXERCISE 5.3 |
| Number Of Questions | 5 |
| Academic Year | 2023-24 |
`triangleABC` and `triangleDBC` are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
(i) `triangleABD ~= triangleACD`
(ii) `triangleABP ~= triangleACP`
(iii) AP bisects `angleA` as well as `angleD`
(iv) AP is the perpendicular bisector of BC.

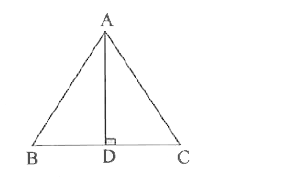
View SolutionAD is an altiude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects A.
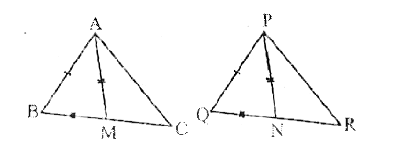
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of `Delta` PQR. Show that
`Delta ABM ~= Delta PQN`
(ii) `Delta ABC ~= Delta PQR`
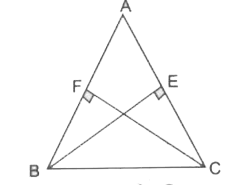
View SolutionBE and CF are two altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
View SolutionABC is an isosceles triangle with AB = AC. Draw `AP bot BC` to show that:
`angleB = angleC`.

View Solution
EXERCISE 5.3 questions and complete solutions for chapter TRIANGLES of CAMBRIDGE MATHS (KANNADA ENGLISH) of Class 9