Complete Solutions to SECTION - A of chapter ICSE EXAMINATION PAPER 2020 of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | ICSE EXAMINATION PAPER 2020 |
| OSWAL | SECTION - A |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
Rationalize the denominatior and simplify to find the value of `(4)/(sqrt(5) + sqrt(3))`
(Given : `sqrt(5) = 2.236 and sqrt(3)` = 1.732)
View SolutionIf `x - (1)/(x) = (1)/(3)`
evaluate `x^(3) - (1)/(x^(3))`
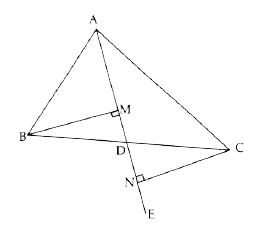
View SolutionIn the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE.
Prove that : (i) `Delta BMD ~= Delta CND` (ii) BM = CN
View SolutionEvaluate : `[(1)/(4)]^(-2)-3(8)^((2)/(3)) xx 4^(0) + [(9)/(16)]^(-(1)/(2))`
View SolutionUsing ruler and compass only :
Construct a rhombus ABCD with AB = 6 cm and diagonal AC = 7 cm.
Hence measure and write down the length of the diagonal BD.
View SolutionMr. Ram borrows Rs. 20,000 for 2 years compounded annually. The rate of interest for the two successive years are 9% and 10% respectively. If he repays Rs. 1,200 at the end of the first year, Rs. 1,660 at the end of second year, find the amount outstanding at the beginning of the third year.
View Solutionusing trigonometric tables evaluate the following :
`(cot 30^(@))/(sec 30^(@)) + ("cosec 30"^(@))/(tan 45^(@)) - (2 cos 0^(@))/(sin 30^(@)) + cos^(2) 45^(@)`
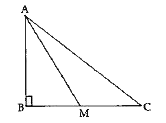
View SolutionABC is a triangle, right angled at B, M is a point on BC. Prove that :
`AM^(2) + BC^(2) = AC^(2) + BM^(2)`
View SolutionConstruct a frequency polygon for the following distribution, using a graph sheet :
`{:("Marks",30-40,40-50,50-60,60-70,70-80,80-90),("No. of students"," "6," "15," "28," "34," "18," "8):}`
View SolutionA is a point on the x-axis and B is (-7, 9). Distance between the points A and B is 15 units. Find the coordinates of point A.
View SolutionIn the given figure, ABCD is a rectangle, whose diagonals intersect at 'O'. Diagonal AC is produced to E and `angle DCE = 145^(@)`.
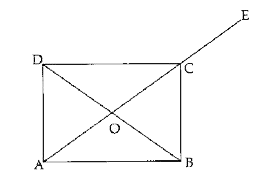
Find : (i) `angle CAB` (ii) `angle AOB`
View SolutionFind the altitude and area of an isosceles triangle whose perimeter is 64 cm and whose base is 24 cm.
View Solution
SECTION - A questions and complete solutions for chapter ICSE EXAMINATION PAPER 2020 of ICSE of Class 9