Complete Solutions to EXERCISE 11 of chapter INEQUALITIES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | INEQUALITIES |
| SELINA PUBLICATION | EXERCISE 11 |
| Number Of Questions | 42 |
| Academic Year | 2023-24 |
From the following figure, prove that : `AB gt CD`
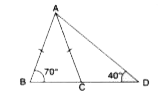
View SolutionIn a triangle PQR, QR = PR and `angleP=36^(@)`. Which is the largest side of the triangle ?
View SolutionIf two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
View SolutionIn each of following figures, write BC, AC and CD in ascending order of their lengths.
(i)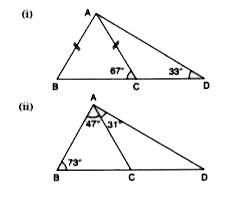
View SolutionArrange the sides of `DeltaBOC` in descending order of their lengths. BO and CO are bisectors of angles ABC and ACB respectively.
View SolutionD is a point in side BC of triangle ABC. If `AD gt AC`, show that `AB gt AC`.
View SolutionIn the following figure, `angleBAC=60^(@)" and "angleABC=65^(@)`.
Prove that :
(i) `CF gt AF" (ii) "DC gt DF`

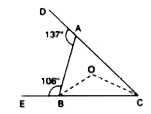
View SolutionIn the following figure ,
AC = CD, `angleBAD=110^(@)" and " angleACB=74^(@)`. Prove that : `BC gt CD`.
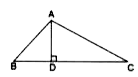
View SolutionFrom the following figure, prove that :
(i) `AB gt BD`
(ii) `AC gt CD`
(iii) `AB+AC gt BC`
View SolutionIn a quadrilateral ABCD, prove that :
(i) `AB+BC+CD gt DA`
(ii) `AB+BC+CD+DA gt 2AC`
(iii) `AB+BC+CD+DA gt 2BD`
View SolutionIn the following figure, ABC is an equilateral triangle and P is any point in AC, prove that :
(i) `BP gt PA`
(ii) `BP gt PC`
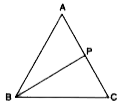
View SolutionP is any point inside the triangle ABC. Prove that : `angleBPC gt angleBAC`.
View SolutionProve that the straight line joining the vertex of an isosceles triangle to any point in the base is smaller than either of the equal sides of the triangle.
View SolutionIn the following diagram, AD = AB and AE bisects angle A. Prove that :
(i) BE = DE (ii) `angleABD gt angleC`
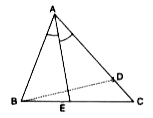
View SolutionThe sides AB and AC of a triangle ABC are produced, and the bisectors of the external angles at B and C meet at P. Prove that if `AB gt AC`, then `PC gt PB`.
View SolutionIn the following figure, AB is the largest side and BC is the smallest side of the triangle ABC.

Write the angles `x^(@), y^(@) " and "z^(@)` in ascending order of their values.
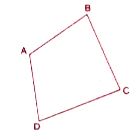
View SolutionIn quadrilateral ABCD, AB is the shortest side and DC is the longest side. Prove that :
(i) `angleB gt angleD`
(ii) `angleA gt angleC`
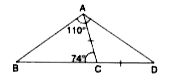
View SolutionIn triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D, prove that : `angleADC` is greater than `angleADB`.
View SolutionIn isosceles triangle ABC, sides AB and AC are equal. If point D lies in base BC and point E lies on BC produced (BC being produced through vertex C), prove that :
(i) `AC gt AD`
(ii) `AE gt AC`
(iii) `AE gt AD`
View SolutionGiven : ED = EC
Prove : `AB+AD gt BC`.

View SolutionIn triangle ABC, `AB gt AC` and D is a point in side BC. Show that : `AB gt AD`.
View SolutionFrom the following figure, prove that : `AB gt CD`

View SolutionIn a triangle PQR, QR = PR and `angleP=36^(@)`. Which is the largest side of the triangle ?
View SolutionIf two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
View SolutionIn each of following figures, write BC, AC and CD in ascending order of their lengths.
(i)
View SolutionArrange the sides of `DeltaBOC` in descending order of their lengths. BO and CO are bisectors of angles ABC and ACB respectively.

View SolutionD is a point in side BC of triangle ABC. If `AD gt AC`, show that `AB gt AC`.
View SolutionIn the following figure, `angleBAC=60^(@)" and "angleABC=65^(@)`.
Prove that :
(i) `CF gt AF" (ii) "DC gt DF`

View SolutionIn the following figure ,
AC = CD, `angleBAD=110^(@)" and " angleACB=74^(@)`. Prove that : `BC gt CD`.

View SolutionFrom the following figure, prove that :
(i) `AB gt BD`
(ii) `AC gt CD`
(iii) `AB+AC gt BC`

View SolutionIn a quadrilateral ABCD, prove that :
(i) `AB+BC+CD gt DA`
(ii) `AB+BC+CD+DA gt 2AC`
(iii) `AB+BC+CD+DA gt 2BD`
View SolutionIn the following figure, ABC is an equilateral triangle and P is any point in AC, prove that :
(i) `BP gt PA`
(ii) `BP gt PC`

View SolutionP is any point inside the triangle ABC. Prove that : `angleBPC gt angleBAC`.
View SolutionProve that the straight line joining the vertex of an isosceles triangle to any point in the base is smaller than either of the equal sides of the triangle.
View SolutionIn the following diagram, AD = AB and AE bisects angle A. Prove that :
(i) BE = DE (ii) `angleABD gt angleC`

View SolutionThe sides AB and AC of a triangle ABC are produced, and the bisectors of the external angles at B and C meet at P. Prove that if `AB gt AC`, then `PC gt PB`.
View SolutionIn the following figure, AB is the largest side and BC is the smallest side of the triangle ABC.

Write the angles `x^(@), y^(@) " and "z^(@)` in ascending order of their values.
View SolutionIn quadrilateral ABCD, side AB is the longest and side DC is the shortest. Prove that :
(i) `angleC gt angleA" (ii) "angleD gt angle B`
View SolutionIn triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D, prove that : `angleADC` is greater than `angleADB`.
View SolutionIn isosceles triangle ABC, sides AB and AC are equal. If point D lies in base BC and point E lies on BC produced (BC being produced through vertex C), prove that :
(i) `AC gt AD`
(ii) `AE gt AC`
(iii) `AE gt AD`
View SolutionGiven : ED = EC
Prove : `AB+AD gt BC`.

View SolutionIn triangle ABC, `AB gt AC` and D is a point in side BC. Show that : `AB gt AD`.
View Solution
EXERCISE 11 questions and complete solutions for chapter INEQUALITIES of ICSE of Class 9