Complete Solutions to QUESTIONS of chapter MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM) of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM) |
| SELINA PUBLICATION | QUESTIONS |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
The figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a (a) parallelogram (b) rectangle (c)square (d) rhombus
View SolutionIn parallelogram PQRS. L is mid-point of side SR and SN is drawn parallel to LQ which meets RQ produced prove that :
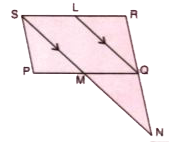
`SP=(1)/(2)RN`
View SolutionIn parallelogram PQRS. L is mid-point of side Sr and SN is drawn parallel to LQ which meets RQ produced prove that :
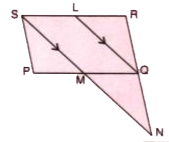
`SN=2LQ`
View SolutionThe adjoining figure shows a parallelogram ABCD in which P is mid-point of AB and Q is mid-point of CD. Prove that `AE=EF=FC`.
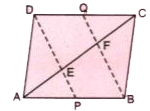
View SolutionIn a right-angled triangle `ABC, angleABC=90^(@)` and D is mid-point of AC. Prove that `BD=(1)/(2)AC`.
View SolutionIn triangle ABC, BE ad CF are median M is a point on BE produced such that BE=EM and N is point on CF produced such that CF=FN. Prove that
NAM is a straight line
View SolutionIn triangle ABC, BE ad CF are median M is a point on BE produced such that BE=EM and N is point on CF produced such that CF=FN. Prove that
A is the mid-point of MN
View SolutionE is the mid-point of the side AD of the tarapezium ABCD with `AB||DC`. A line through E drawn parallel to AB intersects BC at F. Show that F is the mid-points of BC.
View SolutionIn a trapezium ABCD, AB/DC, E is mid-point of aD. A line through E and parallel to AB intersects BC at point F. Show that:
2EF=AB+DC
View SolutionProve by vector method that the line segment joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides and equal to half of their difference.
View SolutionUse the intercept Theorem to prove that the converse of the Mid-point Theorem
View SolutionABCD is a parallelogram. E is the mid-point of AB and F is the mid-point of CD. GH is any line that intersects AD, EF and BC at G, P and H respectively. Prove that : GP=PH

View SolutionUse the information, given in the adjoining figure, to show that AB=AC
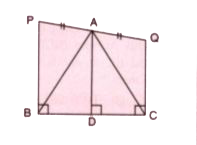
View Solution
QUESTIONS questions and complete solutions for chapter MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM) of ICSE of Class 9