Complete Solutions to EXERCISE 12(A) of chapter MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM) of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM) |
| SELINA PUBLICATION | EXERCISE 12(A) |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
In triangle ABC, M is mid-point of AB and a straight line through M and parallel to BC cuts AC at N. Find the lengths of AN and MN, if BC = 7 cm and AC = 5 cm.
View SolutionProve that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
View SolutionD, E and F are the mid-points of the sides AB, BC and CA of an isosceles triangle ABC in which AB = BC. Prove that `DeltaDEF` is also isosceles.
View SolutionThe following figure shows a trapezium ABCD in which AB // DC. P is the mid-point of AD and PR // AB. Prove that:
`PR = (1)/(2)(AB + CD)`
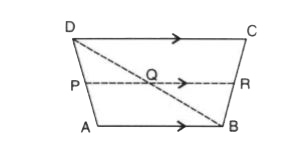
View SolutionThe figure, given below, shows a trapezium ABCD. M and N are the mid-points of the nonparallel sides AD and BC respectively. Find:
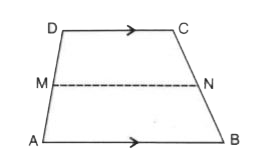
MN, if AB = 11 cm and DC = 8 cm.
View SolutionThe figure, given below, shows a trapezium ABCD. M and N are the mid-points of the nonparallel sides AD and BC respectively. Find:
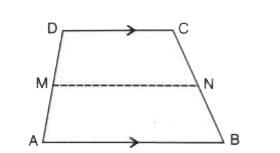
AB, if DC = 20 cm and MN = 27 cm
View SolutionThe figure, given below, shows a trapezium ABCD. M and N are the mid-points of the nonparallel sides AD and BC respectively. Find:
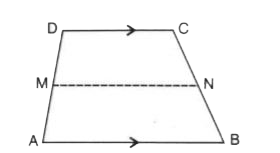
DC, if MN = 15 cm and AB = 23 cm.
View SolutionThe diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
View SolutionL and M are the mid-points of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
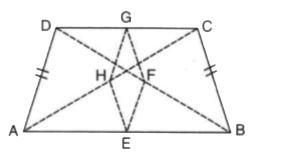
View SolutionABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid-points of AB, BD, CD and AC respectively. Prove that EFGH is a rhombus.
View SolutionA parallelogram ABCD has P the mid-point of DC and Q a midpoint of AC such that `CQ = (1)/(4) AC. PQ` produced meets BC at R. Prove that:
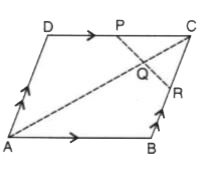
R is the mid-point of BC
View SolutionA parallelogram ABCD has P the mid-point of DC and Q a point of AC such that `CQ = (1)/(4) AC. PQ` produced meets BC at R. Prove that:
`PR=(1)/(2)DB`.
View SolutionD, E and F are the mid-points of the sides AB, BC and CA respectively of A ABC. AE meets DF at O. P and Q are the mid-points of OB and OC respectively. Prove that DPOF is a parallelogram.
View SolutionIn triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q and a line through Q and parallel to BC meets median AP at point R. Prove that :
`AP=2AR`
View SolutionIn triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q and a line through Q and a line through Q and parallel to BC meets median AP at point R. Prove that :
`BC=4QR`.
View SolutionIn trapezium ABCD, AB is parallel to DC. P and Q are the mid-points of AD and BC respectively. BP product meets CD produced at point E. Prove that :
Point P bisects BE,
View SolutionIn trapezium ABCD, AB is parallel to DC. P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E. Prove that :
PQ is parallel to AB.
View SolutionIn a triangle ABC, AD is a median and E is mid-point of median AD. A line through B and E meets AC at point E. Prove that : AC = 3AF Draw DG parallel to BF, which meets AC at point G.
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Prove that BDFE is a parallelogram
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Find AB, if `EF=4.8cm`.
View SolutionIn `Delta` ABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.
View SolutionIn A ABC, E is mid-point of the median AD and BE produced meets side AC at point Q. Show that BE : EQ = 3:1.
View SolutionIn the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF. Show that : EF = AC.
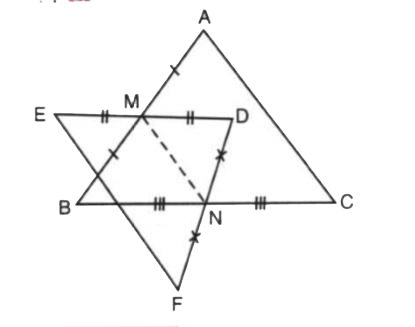
View Solution
EXERCISE 12(A) questions and complete solutions for chapter MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM) of ICSE of Class 9