Complete Solutions to EXERCISE 12(B) of chapter MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM) of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM) |
| SELINA PUBLICATION | EXERCISE 12(B) |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
Use the following figure to find :
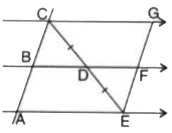
BC, if AB = 7.2 cm.
View SolutionUse the following figure to find :
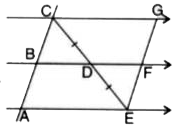
GE, if FE = 4 cm. B
View SolutionUse the following figure to find :
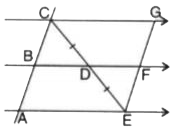
AE, if BD = 4.1 cm.
View SolutionUse the following figure to find :
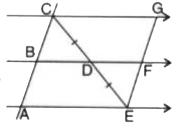
DF, if CG = 11 cm.
View SolutionIn the figure, given below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
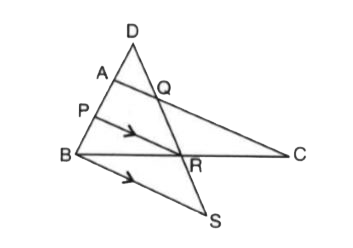
AQ//BS
View SolutionIn the figure, given below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
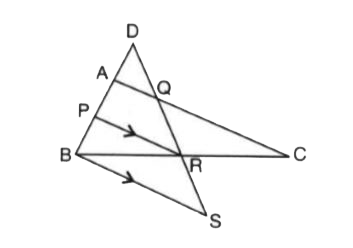
DS=3RS
View SolutionThe side AC of a triangle ABC is produced to point E so that `CE=(1)/(2)` AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:
`3DF=EF`
View SolutionThe side AC of a triangle ABC is produced to point E so that `CE=(1)/(2)` AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:
`4CR=AB`
View SolutionIn triangle ABC, the medians BP and CQ are produced upto points M and N respectively such that BP = PM and CQ = QN. Prove that:
M, A and N are collinear.
View SolutionIn triangle ABC, the medians BP and CQ are produced upto points M and N respectively such that `BP=PM and CQ=QN`. Prove that :
A is the mid-point of MN.
View SolutionIn triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
View SolutionIn parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The lines segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that :
triangle HEB and FHC are congruent.
View SolutionIn parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The lines segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that :
GEHF is a parallelogram.
View SolutionIn triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and Glines are drawn parallel to AB which meet side BC at points M and N respectively.
Prove that : BM = MN = NC.
View SolutionIn triangle ABC, M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use Intercept Theorem to show that MN bisects AD.
View SolutionIf the quadrilateral formed by joining the mid points of the adjacent sides of quadrilateral ABCD is a rectangle, show that the diagonals AC and BD intersect at right angle.
View SolutionIn triangle ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm, find the perimeter of the parallelogram BDEF.
View SolutionIn the given figure, AD and CE are medians and DF||CE. Prove that : `Fb=(1)/(4)AB`.
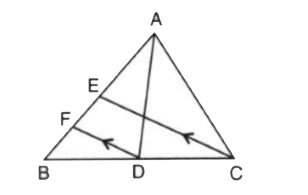
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:
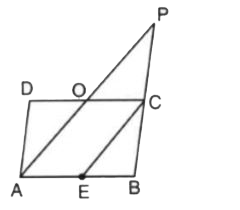
PB=2AD
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:

O is mid-point of AP.
View SolutionIn trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that : AB + DC = 2EF.
View SolutionIn `Delta` ABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.
View SolutionAdjacent sides of a parallelgram are equal and one of diagonls is equal to any one of the sides of this parallelgoram. Show that its diagonals are in the ratio `sqrt(3):1.`
View Solution
EXERCISE 12(B) questions and complete solutions for chapter MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM) of ICSE of Class 9