Complete Solutions to EXERCISE 13(A) of chapter PYTHAGORAS THEORAM of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | PYTHAGORAS THEORAM |
| SELINA PUBLICATION | EXERCISE 13(A) |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
View SolutionA man goes 40 m due north and then 50 m due west. Find his distance from the staring point.
View SolutionIn the figure: `/_PSQ=90^(@), PQ=10 cm, QS=6cm "and " RQ=9 cm`. Find the value of PR.

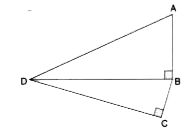
View SolutionThe given figure shows a quadrilateral ABCD in which AD =13 cm, DC= 12 cm, BC=3 cm and `/_ABC= /_BCD=90^(@)`. Calculate the length of AB.
View SolutionAD is draw perendicular to base BC of an equilateral triangle ABC. Given BC=10 cm find the length of AD, correct to 1 place of decimal.
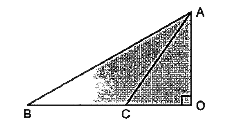
View SolutionIn triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC
View SolutionIn `DeltaABC, AB=AC=x, BC=10cm` and the area of triangle is 60 `cm^(2)`. Find x.
View SolutionIf the sides of a triangle are in the ratio `1 : sqrt(2) : 1`, show that it is a right-angled triangle.
View SolutionTwo poles of heights 6 m and 11 m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
View SolutionIn the given figure, `AB||CD, AB=7cm, BD=25 cm and CD=17cm`, find the length of side BC.

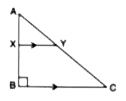
View SolutionIn th given figure, `/_B=90^(@), XY"//"BC, AB=12 cm, AY=8 cm" and "AX : XB=1 : 2= AY : YC`. Find the lenghts of C and BC.
View SolutionIn `triangleABC, /_B=90^(@)`. Find the sides of the triangle if:
`AB=(x-3) cm, BC=(x+4) cm" and "AC=(x+6) cm`.
View SolutionIn `DeltaABC, angleB=90^(@)`, find the sides of the triangle, if :
(i) `AB=(x-3)cm, BC=(x+4)cm and AC=(x+6)cm`
(ii) `AB=xcm, BC=(4x+4)cm and AC=(4x+5)cm`
View Solution
EXERCISE 13(A) questions and complete solutions for chapter PYTHAGORAS THEORAM of ICSE of Class 9