Question

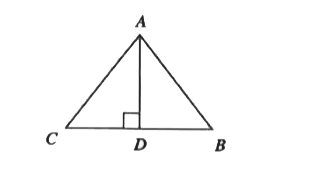
AD is draw perendicular to base BC of an equilateral triangle ABC. Given BC=10 cm find the length of AD, correct to 1 place of decimal.

Answer

`=8.7 cm`

Explanation

To find the length of AD in an equilateral triangle ABC where AD is perpendicular to the base BC and BC = 10 cm, we can follow these steps:

Step 1: Understand the properties of the equilateral triangle
In an equilateral triangle, all sides are equal, and the altitude (perpendicular from a vertex to the opposite side) divides the base into two equal parts.

Step 2: Divide the base BC
Since BC = 10 cm, when we draw the perpendicular AD from A to BC, it divides BC into two equal segments:
- BD = DC = 10 cm / 2 = 5 cm

Step 3: Use the Pythagorean theorem
In triangle ABD, we can apply the Pythagorean theorem:
- AB² = AD² + BD²

Step 4: Substitute the known values
Since AB is a side of the equilateral triangle, AB = 10 cm, and BD = 5 cm:
- (10)² = AD² + (5)²
- 100 = AD² + 25

Step 5: Solve for AD²
Rearranging the equation gives us:
- AD² = 100 - 25
- AD² = 75

Step 6: Find AD
Now, take the square root of both sides to find AD:
- AD = √75
- AD = √(25 × 3) = 5√3

Step 7: Calculate the approximate value of AD
To find the numerical value, we can use the approximation √3 ≈ 1.732:
- AD ≈ 5 × 1.732 ≈ 8.66 cm

Step 8: Round to one decimal place
Finally, rounding 8.66 to one decimal place gives us:
- AD ≈ 8.7 cm

Final Answer:
The length of AD is approximately 8.7 cm.

---