Complete Solutions to Skill Testing Exercise of chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREAS OF PARALLELOGRAMS AND TRIANGLES |
| KUMAR PRAKASHAN | Skill Testing Exercise |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
In a triangle ABC , E is the midpoint of median AD. Show that ar(BED) =`1/4`ar(ABC)

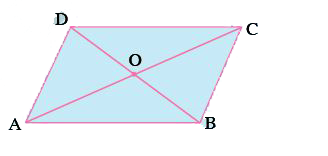
View SolutionABCD is a parallelogram. The diagonals AC and BD intersect each other at ‘O’. Prove that `ar(DeltaAOD) = ar(DeltaBOC)` . (Hint: Congruent figures have equal area)
View SolutionIn `triangleABC`, AD is a median . E is the midpoint of AD and F is the midpoint of AE. Prove that ar(ABF)=`1/8`ar(ABC).
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD (see the given figure). If AQ intersects DP at S and BQ intersects CP at R. Show that:
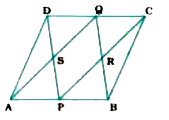
APCQ is a parallelogram.
View SolutionIn parallelogram ABCD, AB=8 cm. The lengths of altitudes corresponding to AB and AD are 4 cm and 5 cm respectively. Find the length of AD.
View SolutionIn parallelogram PQRS. RS=12 cm . The lengths of altitudes corresponding to PQ and QR are 6 cm and 9 cm respectively. Find the length of PS.
View SolutionProve that the area of a rhombus is equal to half of the product of the diagonals.
View Solutionprove that the line segment joining the midpoints of two opposite sides of a parallelogram divides the parallelogram into two parallelograms with equal area.
View SolutionIn quadrilateral ABCD, AM and CN are altitudes on diagonal BD drawn from A and C respectively .Prove that
ar(ABCD)=`1/2` BD(AM+CN)
View SolutionIn the given figure, ABED is a parallelogram and DE and EC . Prove that ar (ABF)=ar(BEC)

View SolutionIn `triangleABC`, point D lies on side BC. E is the midpoint of AD. Prove that,
ar(EBC)=`1/2`ar(ABC)
View SolutionIn `triangleABC`, point D lies on side BC. E is the midpoint of AD. Prove that,
ar(EBC)=`1/2`ar(ABC)
View Solution
Skill Testing Exercise questions and complete solutions for chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 9