In △ABC, AD is a median . E is the midpoint of AD and F is the midpoint of AE. Prove that ar(ABF)=18ar(ABC). Solution in Gujrati
Step by step video & image solution for In triangleABC, AD is a median . E is the midpoint of AD and F is the midpoint of AE. Prove that ar(ABF)=1/8ar(ABC). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - KUMAR PRAKASHANCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Multiple Choice Questions (MCQs)
17 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - KUMAR PRAKASHANCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Sum to Enrich Remember
4 Videos
- BOARD'S SAMPLE QUESTION PAPERS (QUESTION PAPER 1 : FOR THE FIRST TEST) BOOK - KUMAR PRAKASHANCHAPTER - BOARD'S SAMPLE QUESTION PAPERS (QUESTION PAPER 1 : FOR THE FIRST TEST) EXERCISE - Section D (Solve the following)
4 Videos
Similar Questions
Area of a parallelogram =_____
View SolutionIn the given figure, ABED is a parallelogram and DE and EC . Prove that ar (ABF)=ar(BEC)

View SolutionYamini and Fatima , two students of class IX of a school, together contributed Rs 100 towards the prime Minister's Relief Fund to help the earthquake victims . Write a linear equation which satisfies this this data. (You may take their contributions as Rs x and Rs y). Draw the graph of the same.
View SolutionIn an equilateral ΔABC,D is the midpoint of AB and E is the midpoint of AC. Then, ar(ΔABC):ar(ΔADE)=?

View SolutionΔABC में, E मध्यिका AD का मध्य - बिंदु है । दर्शाइए कि ar(BED)=14ar(ABC) है।
View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).

View SolutionThe vertex A of △ABC is joined to a point D on the side BC. The midpoint of AD is E.
Prove that ar(△BEC)=12ar(△ABC).
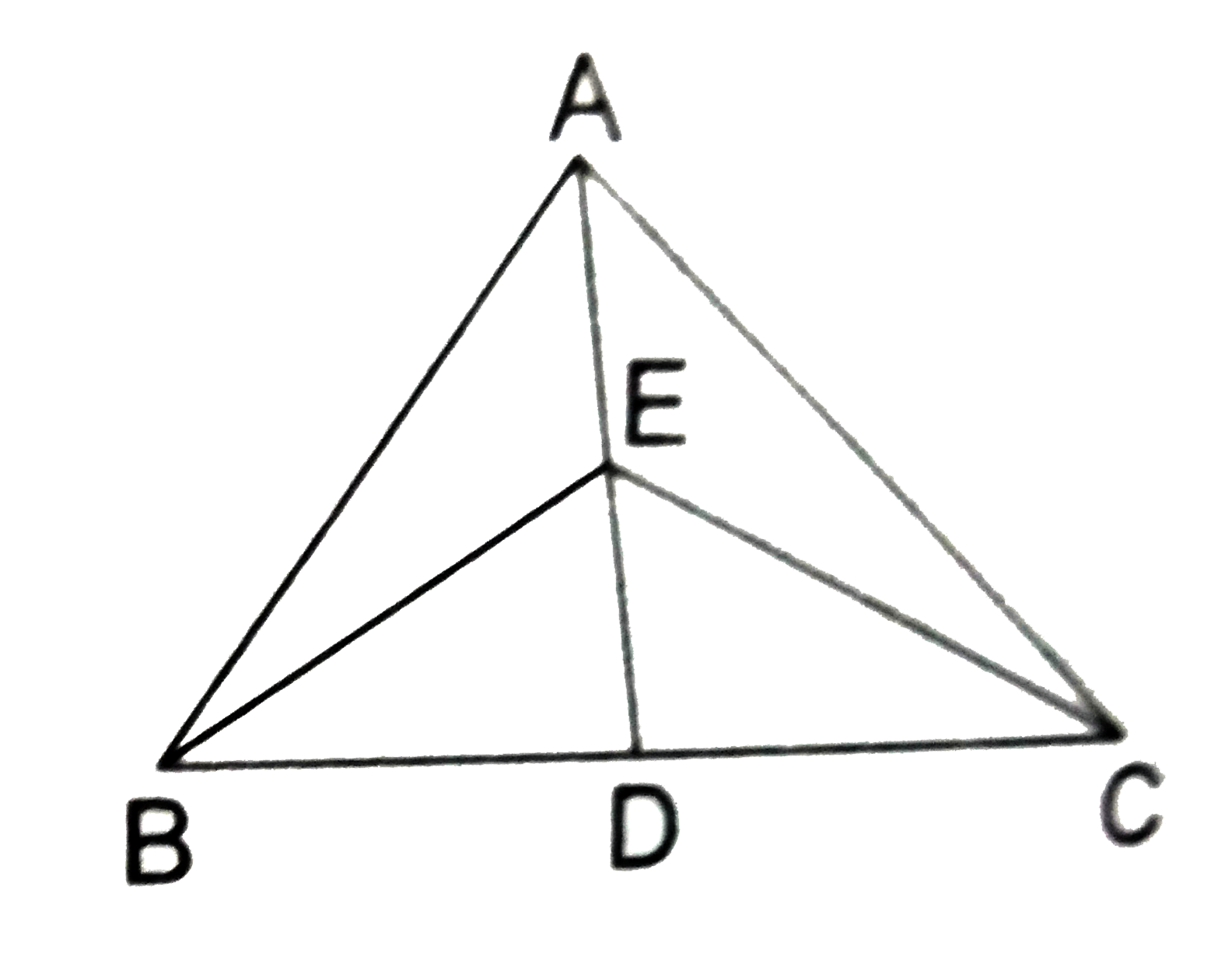
View SolutionD is the midpoint of side BC of △ABC and E is the midpoint of BD. If O is the midpoint of AE,
prove that ar(△BOE)=18ar(△ABC).
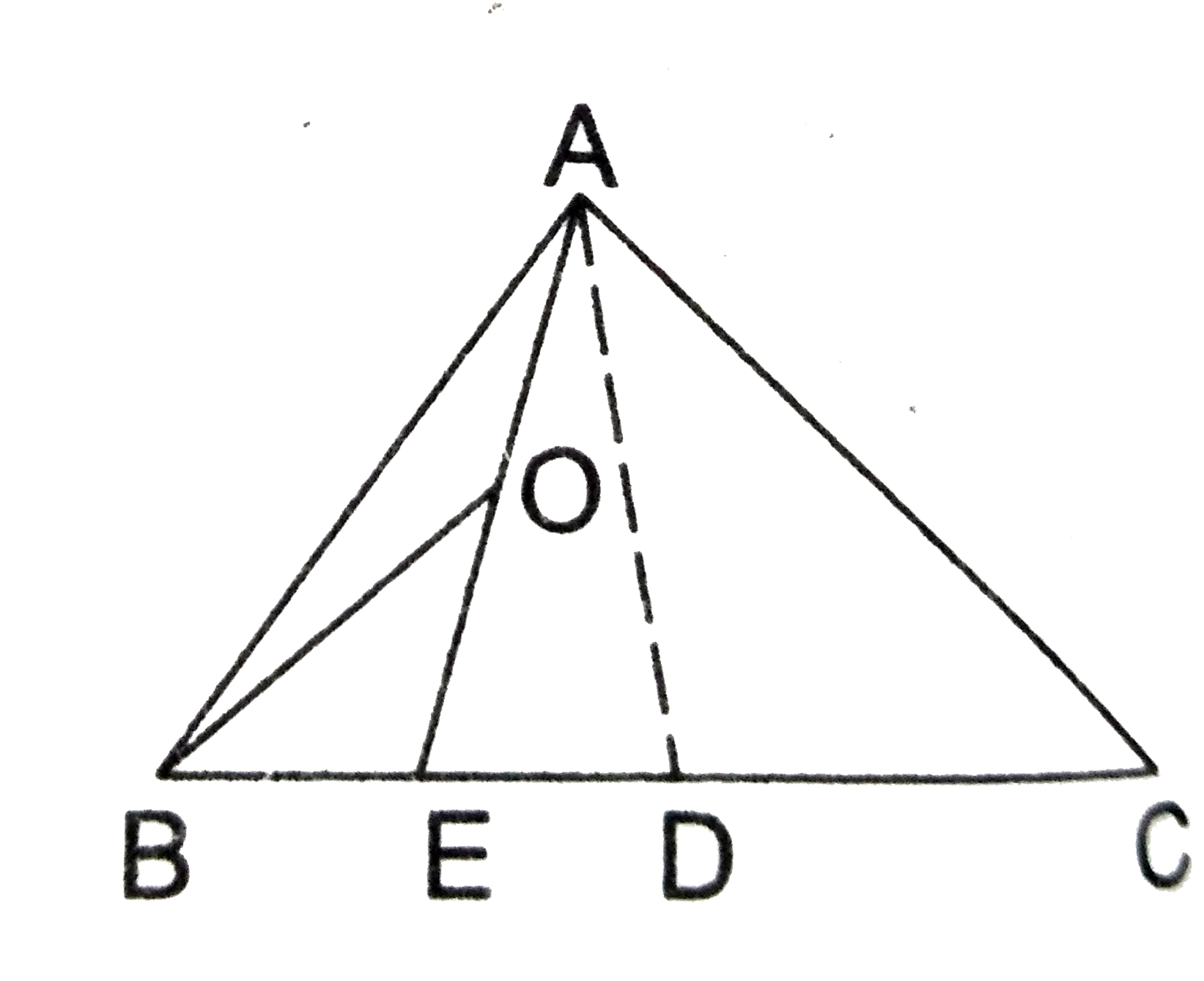
View SolutionIn △ABC, if D is the midpoint of BC and E is the midpoint of AD then ar(△BED) = ?

View Solutionत्रिभुज ABC में D व E क्रमशः भुजा BC व माध्यिका AD के मध्य बिंदु है। यदि ar(ΔAEC)=4 वर्ग सेमी हो, तो ar(ΔBEC)=
View SolutionΔABC में, E माध्यिका AD का मध्य-बिन्दु है। दर्शाइए कि ar(BED)=14ar(ABC) है।
View Solution△ABC में, E माध्यिका AD का मध्य -बिन्दु है । दर्शाइए कि -
ar(BED)=14ar(ABC)
View Solution△ABC की माध्यिका AD पर स्थित कोई बिन्दु E है। दर्शाइए कि -ar(△ABE)=ar(△ACE)
View SolutionIn a triangle ABC (see figure), E is the midpoint of median AD, show that
(i) ar ΔABE=arΔACE
(ii) arΔABE=14ar(ΔABC)
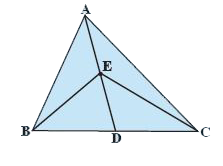
View SolutionIn a triangle ABC (see figure), E is the midpoint of median AD, show that (i) ar DeltaABE = ar DeltaACE (ii) ar DeltaABE=1/4ar(DeltaABC)
View Solution
