Doubtnut Promotions Sticky

Complete Solutions to प्रश्नावली 9 (C) of chapter समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of Class 9 book with complete answers and questions

Class 9MATHS
Chapterसमान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
MANOHAR RAYप्रश्नावली 9 (C)
Number Of Questions4
Academic Year2023-24

  1. एक चतुर्भुज ABCD का BD एक विकर्ण है। भुजा BD पर AM तथा CN डालें गये लम्ब है। सिद्ध कीजिए कि
    क्षेत्रफल `(ABCD)=(1)/(2)BD(AM+CN)`

    01:52
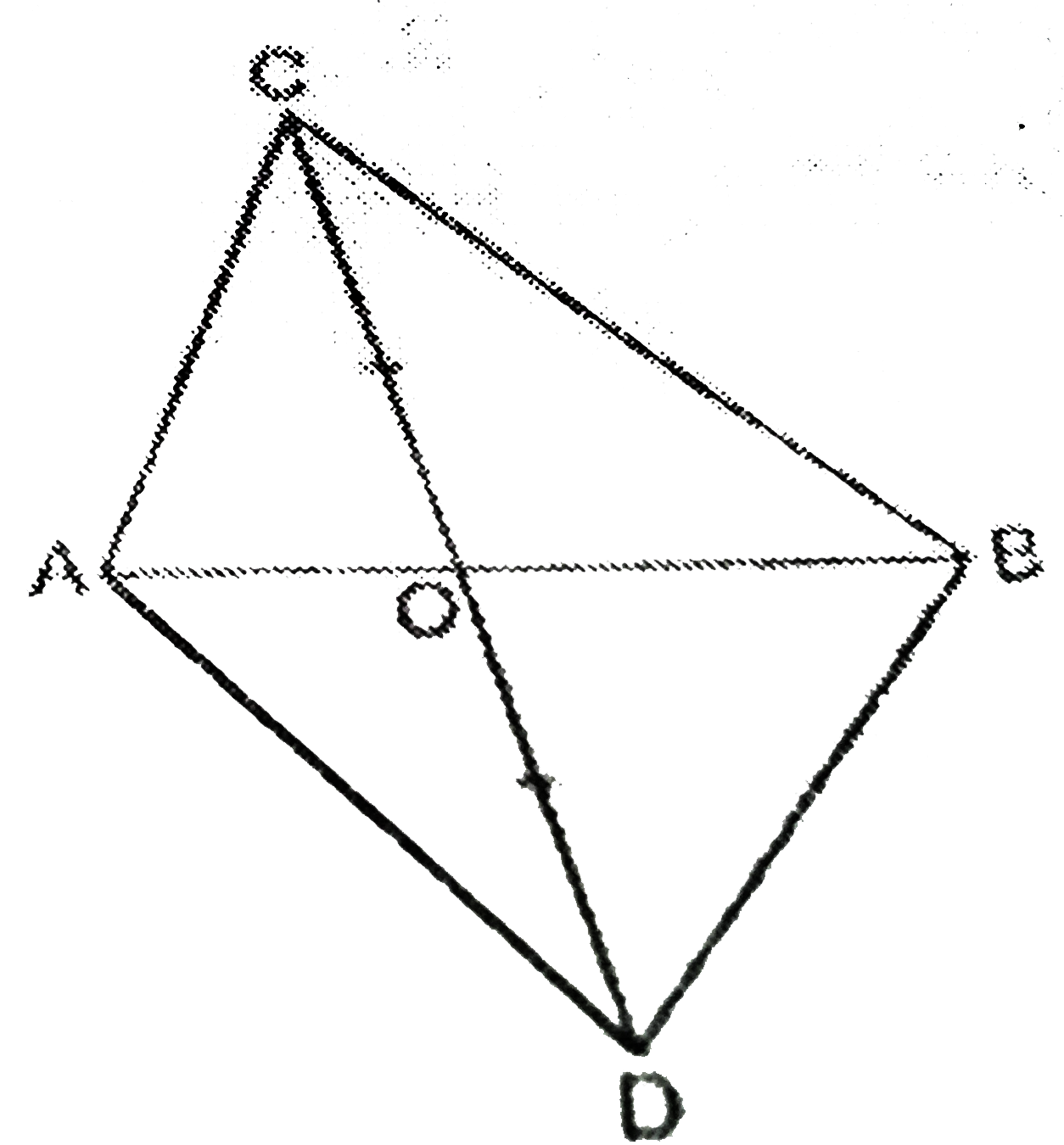
    View Solution

  2. आकृति में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज है। यदि रेखाखंड CD रेखाखंड AB से बिन्दु O पर समद्विभाजित होता है, तो दर्शाइए कि क्षेत्रफल (ABC) = क्षेत्रफल (ABD) है।

    05:26
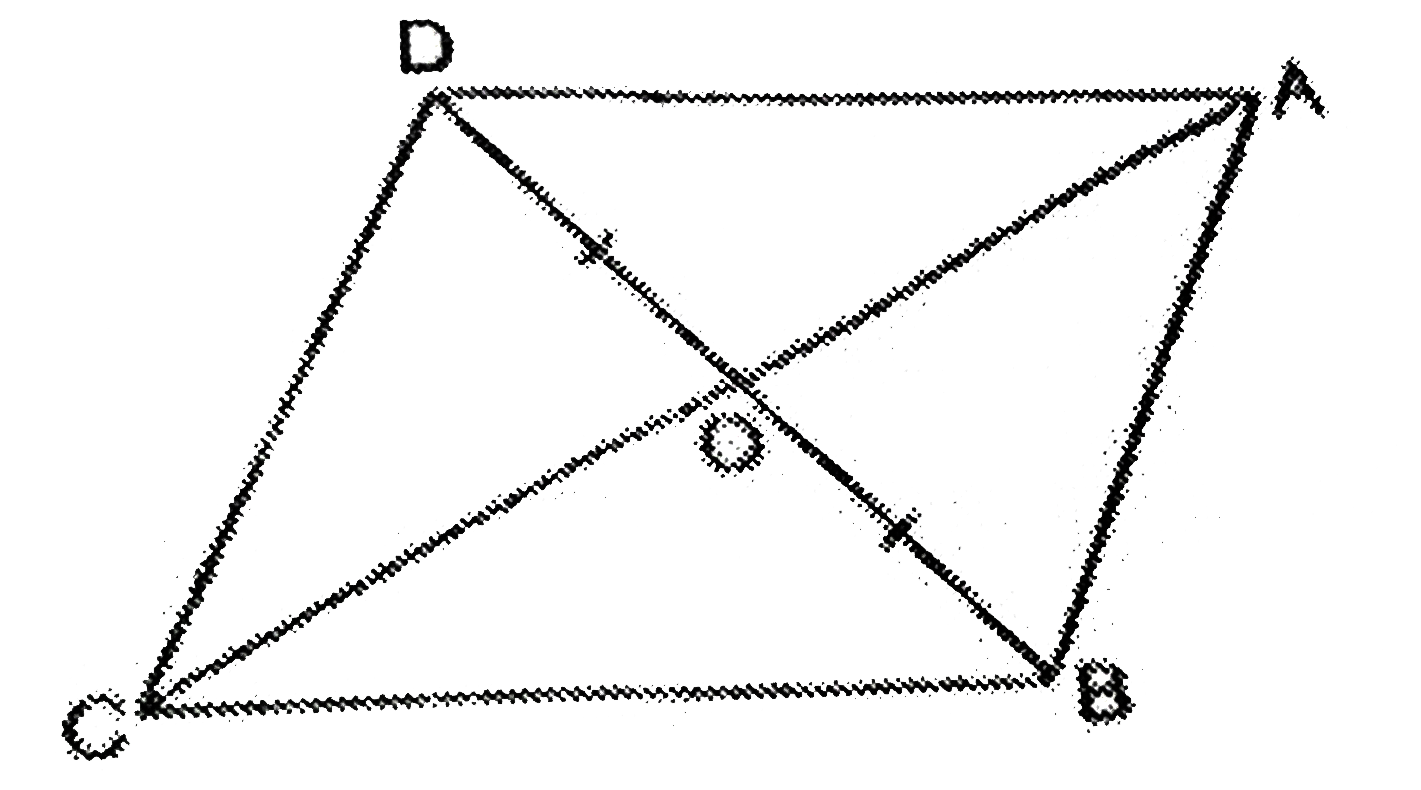
    View Solution

  3. आकृति में, चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते है कि OB=OD है। यदि AB=CD है, तो दर्शाइए कि
    (i) क्षेत्रफल (DOC) = क्षेत्रफल (AOB)
    (ii) क्षेत्रफल (DOB) = क्षेत्रफल (ACB)
    (iii) `DA||CB` या ABCD एक समांतर चतुर्भुज है।

    10:37
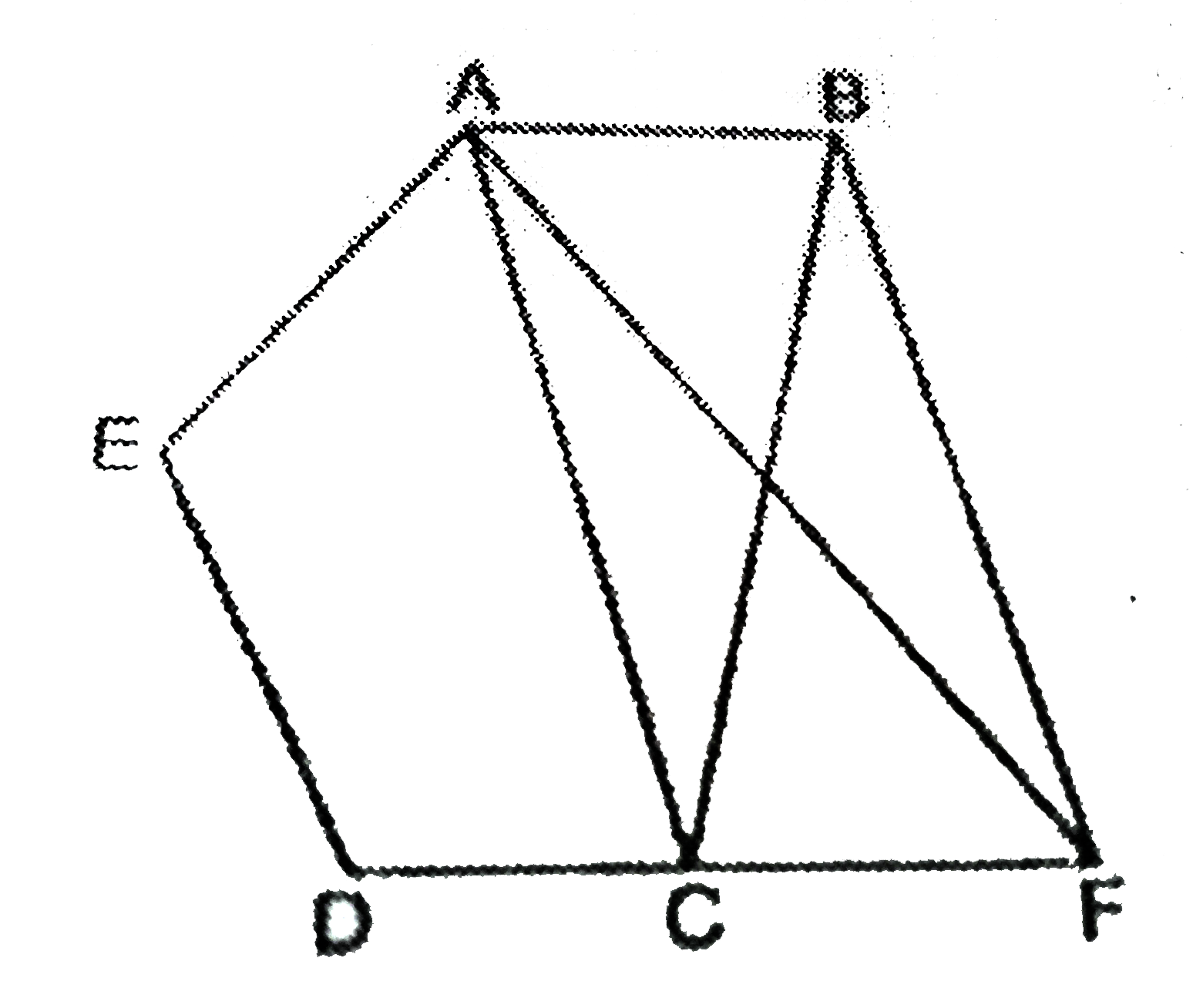
    View Solution

  4. आकृति में, ABCDE एक पंचभुज है। B से होकर AC के समांतर खींची गई रेखा बढाई गई DC को F पर मिलती है। दर्शाइए कि
    (i) क्षेत्रफल (ACB) = क्षेत्रफल (ACF)
    (ii) क्षेत्रफल (AEDF) = क्षेत्रफल (ABCDE)

    03:58
    View Solution

प्रश्नावली 9 (C) questions and complete solutions for chapter समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of DR MANOHAR RAY MATHS (HINDI) of Class 9