Complete Solutions to प्रश्नावली 9(D) of chapter समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल |
| MANOHAR RAY | प्रश्नावली 9(D) |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
एक त्रिभुज का क्षेत्रफल `6sqrt2" सेमी "^(2)` है और आधार की लम्बाई 3 सेमी है। त्रिभुज की ऊंचाई होगी :
View Solutionएक समलम्ब चतुर्भुज की समान्तर भुजाएँ 2 सेमी और 5 सेमी है, उनके बीच की दूरी 4 सेमी है। समलम्ब का क्षेत्रफल होगा :
View Solutionत्रिभुज की कोई माध्यिका उसे दो भागो में बांटती है, तो उनके क्षेत्रफल होते है :
View Solutionसमचतुर्भुज का क्षेत्रफल, उसके विकर्णों के गुणनफल का होता है
View Solutionकिसी समान्तर चतुर्भुज का एक विकर्ण उसे बाँटता है :
View Solutionसमांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्तिथ है और उनके क्षेत्रफल बराबर है। दर्शाइए कि समांतर चतुर्भुज का परिमाण आयत के परिमाप से अधिक है।
View Solutionआकृति में, भुजा BC पर दो बिन्दु D और E इस प्रकार स्थित है कि BD= DC= EC है। दर्शाइए कि ar (ABD) = ar (ADE) =ar (AEC) है।

View Solutionआकृति में, ABCD, DCFE और ABFE समांतर चतुर्भुज है। दर्शाइए कि ar (ADE) = ar (BCF) है।

View Solutionआकृति में ABCD एक समांतर चतुर्भुज है और BC को एक बिन्दु Q तक इस प्रकार बढ़ाया गया है कि AD=CQ है। यदि AQ भुजा DC को P पर प्रतिच्छेद करती है तो दर्शाइए कि ar (BPC) = ar (DPQ) है।
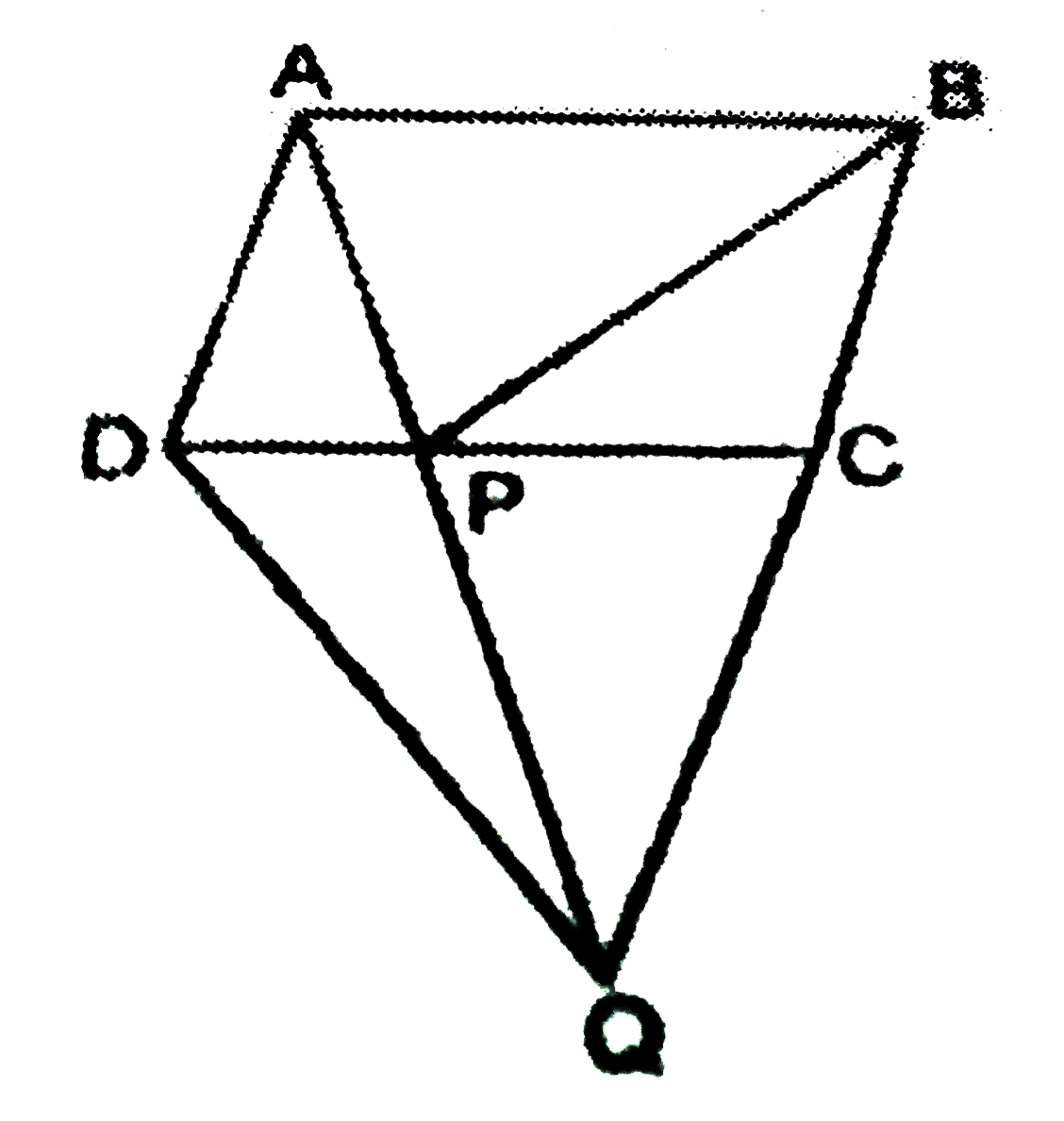
View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते है। दर्शाइए कि
`"ar"(APB)xx"ar"(CPD)="ar"(APD)xx"ar"(BPC)`
View Solution
प्रश्नावली 9(D) questions and complete solutions for chapter समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of DR MANOHAR RAY MATHS (HINDI) of Class 9