Complete Solutions to प्रश्नावली 9(C) of chapter समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल |
| MANOHAR RAY | प्रश्नावली 9(C) |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
यदि किसी समचतुर्भुज के विकर्ण क्रमशः 12 सेमी और 16 सेमी हो, तो उसका क्षेत्रफल तथा भुजा ज्ञात कीजिए।
04:21View Solutionकिसी समलम्ब का क्षेत्रफल 78 वर्ग सेमी तथा समान्तर भुजाओं के बीच की दूरी 6 सेमी है। समान्तर भुजाओं का योगफल ज्ञात कीजिए।
03:00View Solutionएक समान्तर चतुर्भुज की कोई भुजा 8 सेमी है। यदि उस समान्तर चतुर्भुज का क्षेत्रफल 40 वर्ग सेमी हो, तो ज्ञात भुजा के समान्तर भुजा की दूरी की गणना कीजिए।
02:21View Solutionयदि दो त्रिभुजों के आधार समान हो तथा उनके शीर्ष समान्तर रेखाओं के एक ही युग्म पर स्थित हो तो उन त्रिभुजों के क्षेत्रफल समान होते है।
02:33View Solutionदिये चित्र में `(DeltaABC)` की भुजा AB और AC पर क्रमशः D और E बिन्दु इस प्रकार है कि क्षेत्रफल `(DeltaBCE)` = क्षेत्रफल `(DeltaBCD)` तथा सिद्ध कीजिए कि `DE||BC`.
01:57View Solution`DeltaABC` की माध्यिकाएँ G बिन्दु पर प्रतिच्छेद करती है। सिद्ध कीजिए कि क्षेत्रफल `(DeltaAGB)=(1)/(3)` क्षेत्रफल `(DeltaABC)`.
08:22View Solutionयदि एक चतुर्भुज का प्रत्येक विकर्ण उसे समान क्षेत्रफल वाले दो त्रिभुजों में बांटता है , तो दिखाओ कि चतुर्भुज एक समान्तर चतुर्भुज है।
07:17View Solutionएक समषटभुज ABCDEF में AD, BE और CF का प्रतिच्छेद बिन्दु O है। सिद्ध कीजिए की
क्षेत्रफल `(DeltaAOB)=(1)/(6)` क्षेत्रफल (सष्र्टभुज ABCDEF).03:37View Solutionएक त्रिभुज ABC में, BC का मध्य बिन्दु D है और AD का मध्य बिन्दु E है। सिद्ध कीजिए :
क्षेत्रफल `(DeltaBED)=(1)/(4)" क्षेत्रफल "(DeltaABC)`.
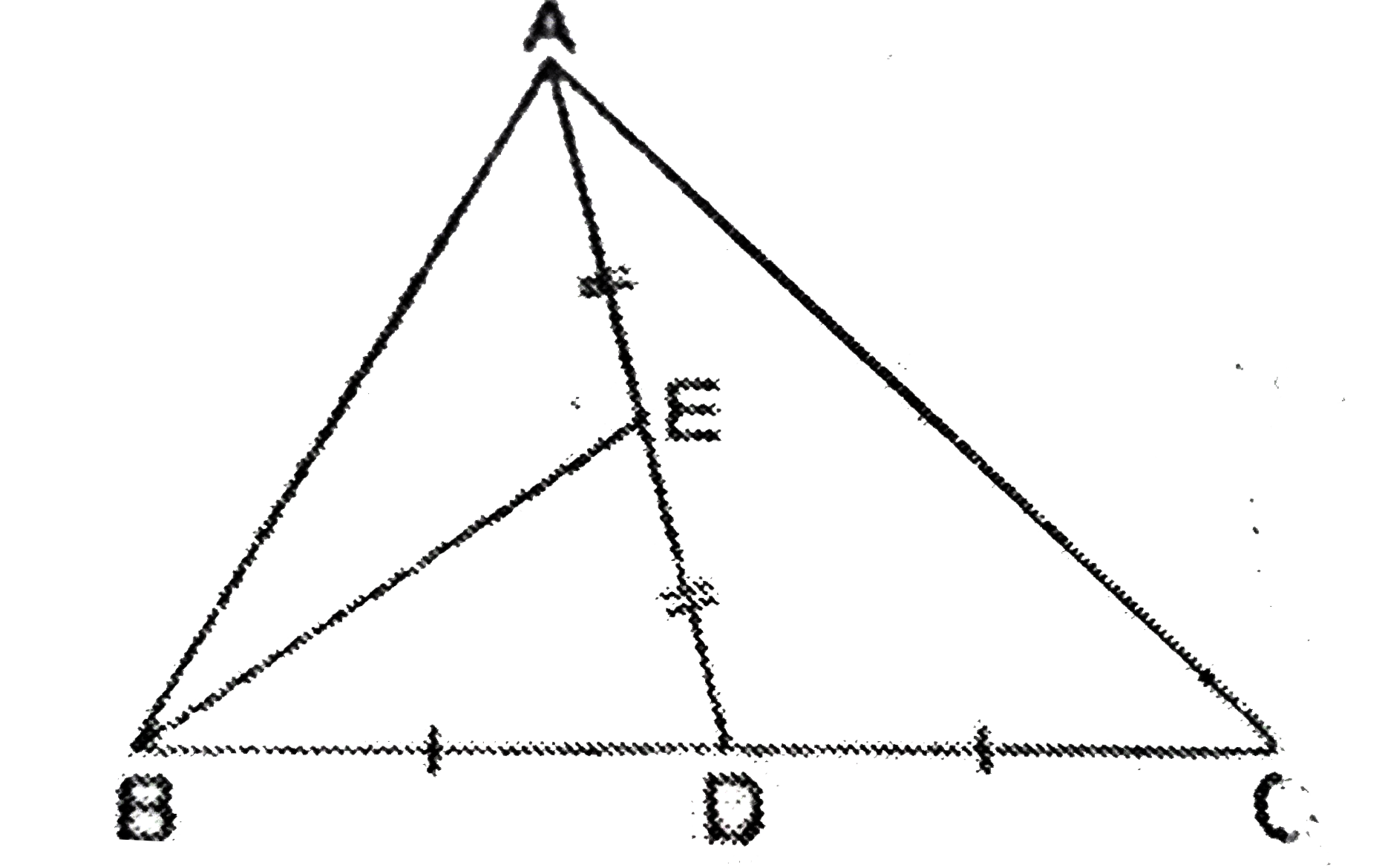
03:09View SolutionD, E और F क्रमशः त्रिभुज ABC की भुजाओ BC, CA और AB के मध्य - बिन्दु है। दर्शाइए कि
(i) BDEF एक समांतर चतुर्भुज है
(ii) क्षेत्रफल `(DEF)=(1)/(4)` क्षेत्रफल (ABC)
(iii) क्षेत्रफल `(BDEF)=(1)/(2)` क्षेत्रफल (ABC)06:49View SolutionXY त्रिभुज ABC की भुज BC के समांतर एक रेखा है। यदि `BE||AC` और `CF||AB` रेखा XY से क्रमशः E और F पर मिलती है, तो दर्शाइए कि
क्षेत्रफल (ABE) = क्षेत्रफल (ACE).02:54View Solutionसमांतर चतुर्भुज ABCD की एक भुजा AB को एक बिन्दु P तक बढ़ाया गया है। A से होकर CP के समांतर खींची गई रेखा बढ़ाई गई CB को Q पर मिलती है और फिर समांतर चतुर्भुज PBQP को पूरा किया गया है (देखिए आकृति )। दर्शाइए कि (ABCD ) = क्षेत्रफल (PBQR ) है।
03:47View Solutionएक समलंब ABCD जिसमे `AB||DC` है के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते है। दर्शाइए कि क्षेत्रफल (AOD) = क्षेत्रफल (BOD) है।
05:30View Solutionगाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड तथा। उस गाँव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध के साथ स्वीकार कर लेते है कि उसे इस भाग के बदले उसी भूखंड के संग्लन एक भाग ऐसे दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
03:03View SolutionABCD एक समलंब है, जिसमे `AB||DC` है। AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है। सिद्ध कीजिए कि क्षेत्रफल (ADX) = क्षेत्रफल (ACY) है।
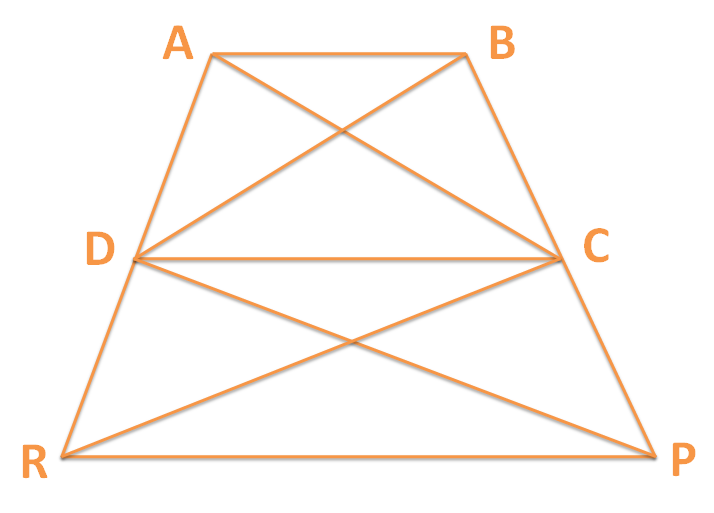
04:27View Solutionआकृति में, `AP||BQ||CR` है। सिद्ध कीजिए कि क्षेत्रफल (AQC) = क्षेत्रफल (PBR) है।
04:44View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते है कि क्षेत्रफल (AOD) = क्षेत्रफल (BOC) है। सिद्ध कीजिए कि ABCD एक समलंब है।
04:11View Solutionआकृति में, क्षेत्रफल `(DRC)` = क्षेत्रफल `(DPC)` है और क्षेत्रफल `(BDP)` = क्षेत्रफल `(ARC)` है। दर्शाइए कि दोनों चतुर्भुज `ABCD` और `DCPR` समलंब हैं।
06:13View Solution
प्रश्नावली 9(C) questions and complete solutions for chapter समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of DR MANOHAR RAY MATHS (HINDI) of Class 9