Complete Solutions to Exercise of chapter Triangles of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | Triangles |
| MBD | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
In Fig.
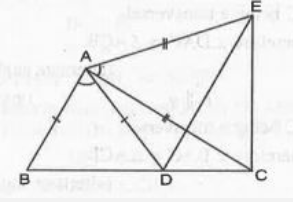
AC = AE, AB = AD and `angleBAD = angleEAC`. Show that BC = DE.
View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AB such that `angleBAD = angleABE` and `angleEPA = angleDPB`. Show that `DeltaDAP ~= DeltaEBP`.

View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AB such that `angleBAD = angleABE` and `angleEPA = angleDPB`. Show that AD=BE.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : `DeltaAMC ~= DeltaBMD`.
) Show that : `DeltaAMC ~= DeltaBMD`.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.)

Show that : `angleDBC` is a right angle.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : `DeltaAMC ~= DeltaBMD`.
) Show that : `DeltaAMC ~= DeltaBMD`.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.)

Show that : `CM=1/2AB`.
View SolutionThe following pairs of triangles are congruent ? `DeltaABC` and `DeltaPQR` in which AB=PQ, BC=QR and `angleC=angleR`.
View SolutionThe following pairs of triangles are congruent ? `DeltaABC` and `DeltaDEF` in which BC=EF, AC=DF and `angleC=angleF`.
View SolutionThe following pairs of triangles are congruent ? `DeltaABC` and `DeltaXYZ` in which `angleA=angleX=90^@` AB=XY, `angleC= 40^@` and `angleY=50^@`.
View SolutionIn an isosclees triangle ABC, with AB = AC, the bisectors of `angleB` and `angleC` intersect each other at O. Join A to O show that : OB=OC.
View SolutionIn an isosclees triangle ABC, with AB = AC, the bisectors of `angleB` and `angleC` intersect each other at O. Join A to O show that : AO bisects `angleA`.
View SolutionIn `DeltaABC`, AD is the perpendicular bisector of BC (See Fig.
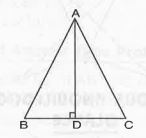 ). Show that `DeltaABC` is an isosceles triangle in which AB = AC.
). Show that `DeltaABC` is an isosceles triangle in which AB = AC.
View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively (See Fig.
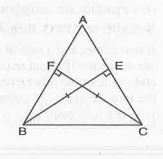 ). Show that these altitudes are equal.
). Show that these altitudes are equal.
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (See Fig.
 ). Show that `DeltaABE ~= DeltaACF`.
). Show that `DeltaABE ~= DeltaACF`.
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (See Fig.
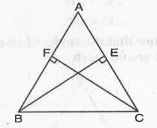 ). Show that AB = AC or `DeltaABC` is an isosceles triangle.
). Show that AB = AC or `DeltaABC` is an isosceles triangle.
View SolutionABC and DBC are two isosceles triangles on the same base BC (See Fig.
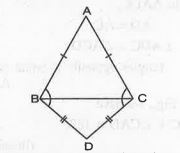 ). Show that `angleABD = angleACD`.
). Show that `angleABD = angleACD`.
View Solution`DeltaABC` is an isoscelestriangle in which AB = AC. Side BA is produced to D such that AD = AB. Show that `angleBCD` is a right angle (see Fig.
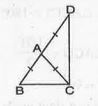 ).
).
View SolutionABC is a right angled triangle in which `angleA = 90^@` and AB = AC. Find `angleB` and `angleC`.
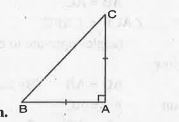
View SolutionShow that the angles of an equilateral triangle are `60^@` each.
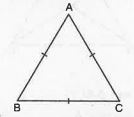
View SolutionIf vertical angle of an isosceles triangle is `40^@`. Find the measure of other two angles.
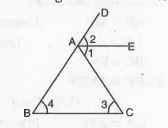
View SolutionIn given Fig.
 , AD = AE and D and E are points on BC, such that BD = EC. Prove that AB = AC.
, AD = AE and D and E are points on BC, such that BD = EC. Prove that AB = AC.
View SolutionIf in given Fig.
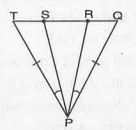 , PQ = PT and `angleTPS = angleQPR`, Prove that triangle PRS is isosceles.
, PQ = PT and `angleTPS = angleQPR`, Prove that triangle PRS is isosceles.
View SolutionAngles A, B and C of a triangle ABC are equal to each other. Prove that `DeltaABC` is equilateral.
View SolutionIf the bisector of an angle of a triangle also bisects the opposite side, prove that triangle is isosceles.
View SolutionIf the base of an isosceles triangle is produced both ways, show that the exterior angles so formed are equal.
View SolutionIf the bisector of the exterior vertical angle of a triangle be parrallel to the base, show that the triangle is isosceles.
View SolutionABCD is a square and DEC is an equilateral triangle. Prove that AE = BE.
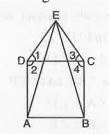
View Solution`DeltaABC` and `DeltaDBC` are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
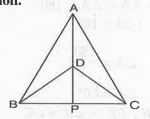 ).If AD is extended to intersect BC at P, show that `DeltaABD ~= DeltaACD`.
).If AD is extended to intersect BC at P, show that `DeltaABD ~= DeltaACD`.
View Solution`DeltaABC` and `DeltaDBC` are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
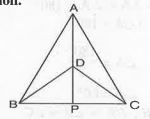 ).If AD is extended to intersect BC at P, show that `DeltaABP ~= DeltaACP`.
).If AD is extended to intersect BC at P, show that `DeltaABP ~= DeltaACP`.
View Solution`DeltaABC` and `DeltaDBC` are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
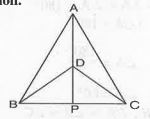 ).If AD is extended to intersect BC at P, show that AP bisects `angleA` as well as `angleD`.
).If AD is extended to intersect BC at P, show that AP bisects `angleA` as well as `angleD`.
View Solution`DeltaABC` and `DeltaDBC` are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
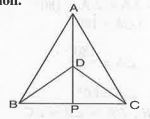 ).If AD is extended to intersect BC at P, show that AP is the perpendicular bisector of BC.
).If AD is extended to intersect BC at P, show that AP is the perpendicular bisector of BC.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that AD bisects BC.
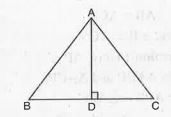
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that:- AD bisects `angle A`.
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of `DeltaPQR` (See Fig
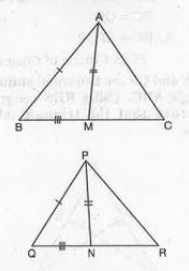 ). Show that : `DeltaABM ~= DeltaPQN`.
). Show that : `DeltaABM ~= DeltaPQN`.
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of `DeltaPQR` (See Fig
 ). Show that : `DeltaABC ~=DeltaPQR`.
). Show that : `DeltaABC ~=DeltaPQR`.
View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

View SolutionABC is an isosceles triangle with AB = AC. Draw `AP bot BC` to show that `angle B = angle C`.
View SolutionP is a point equidistant from two lines `l` and `m` intersecting at point A (see Fig.
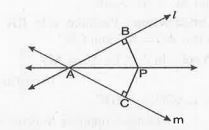 ). Show that the line AP bisects `angleBAC`.
). Show that the line AP bisects `angleBAC`.
View SolutionThe image of an object placed at a point before a plane mirror LM is seen at the point B by an observer at D as shown in the given fig.
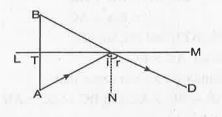
Prove that the image is as far behind the mirror as the object is in front of the mirror.
View SolutionShow that in a right angled triangle, the hypotenuse is the longest side.
View SolutionIn Fig.
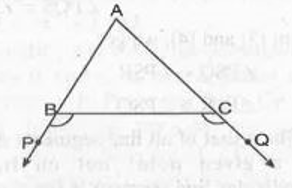 , sides AB and AC of `DeltaABC` are extended to points P and Q respectively. Also `anglePBC < angleQCB`. Show that `AC > AB`.
, sides AB and AC of `DeltaABC` are extended to points P and Q respectively. Also `anglePBC < angleQCB`. Show that `AC > AB`.
View SolutionIn Fig.
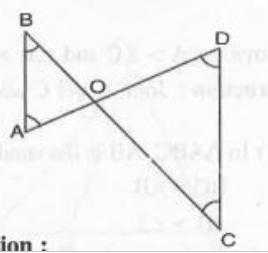 , `angleB < angleA` and `angleC < angleD`. Show that `AD < BC`.
, `angleB < angleA` and `angleC < angleD`. Show that `AD < BC`.
View SolutionIn `DeltaABC`, BC = 3.6 cm, CA = 2.8 cm. AB = 3.4 cm, arrange the angles in order of their measurement.
View SolutionIn `DeltaABC` if `angleA = 48^@`, `angleB = 51^@`, find the third angle and name the greatest side.
View SolutionIn `DeltaABC` if `angleA = angleB=62frac(1^@) 2`, find the third angle and name the shortest side.
View SolutionIn the Fig.
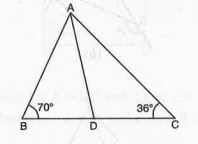
If `AB = AD`. Prove that `AB > CD`.
View SolutionABC is an equilateral triangle. X is point on AC, Prove that `BX > XC` and `BX > AX`.
View SolutionIn given Fig.
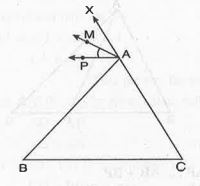 , ABC is a triangle with base BC. If the base angles of `DeltaABC` are `75^@` and `55^@`, state which of two is `75^@` ? If AM bisects the exterior angle `angleBAX` and `AP II CB` find `angleMAP`.
, ABC is a triangle with base BC. If the base angles of `DeltaABC` are `75^@` and `55^@`, state which of two is `75^@` ? If AM bisects the exterior angle `angleBAX` and `AP II CB` find `angleMAP`.
View SolutionIn `DeltaABC`, `AC > AB` and AD is a median. Prove that `angleBAD < angleCAD`.
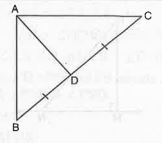
View SolutionIn fig.
 BP and CP are the bisectors of `angleB` and `angleC` respectively and AC > AB. Prove each of the following : `PC>PB`.
BP and CP are the bisectors of `angleB` and `angleC` respectively and AC > AB. Prove each of the following : `PC>PB`.
View SolutionIn fig.
 BP and CP are the bisectors of `angleB` and `angleC` respectively and AC > AB. Prove each of the following : `PC>PB`.
BP and CP are the bisectors of `angleB` and `angleC` respectively and AC > AB. Prove each of the following : `PC>PB`.
View SolutionIn fig.
 BP and CP are the bisectors of `angleB` and `angleC` respectively and AC > AB. Prove each of the following : `PC>PB`.
BP and CP are the bisectors of `angleB` and `angleC` respectively and AC > AB. Prove each of the following : `PC>PB`.
View SolutionOf all the line segments drawn from a point P to `a` line `l` not containing P, let PD be the shortest. If B and C are points on `l` such that D is the mid-point of BC, prove that PB = PC.
View SolutionIn `DeltaABC`, `AC > AB`. The bisector of `angleA` meets BC at D. Prove that `angleADB` is an acute angle.
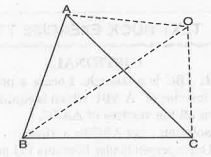
View SolutionO is any point in the exterior of a `DeltaABC`. Prove that `2(OA + OB + OC) > (AB + BC + CA)`
 .
.
View SolutionProve that the difference of any two sides of a triangle is less than the third side.
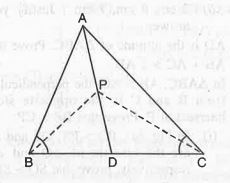
View SolutionIn Fig.
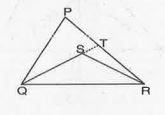 , PQR is a triangle, S is any point in its interior, show that . `SQ + SR < PQ + PR`.
, PQR is a triangle, S is any point in its interior, show that . `SQ + SR < PQ + PR`.
View SolutionIn Fig.
 ,
,
`AB > AC`, show that `AB > AD`.
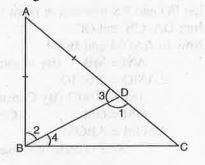
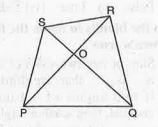
View SolutionFind x+y+z
View SolutionDiagonals PR and QS of a quadrilateral PQRS intersect each other at O. Prove that `PR + QR + RS + SP < 2 (PR + QS)`.
View SolutionDiagonals PR and QS of a quadrilateral PQRS intersect each other at O. Prove that `PR + QR + RS + SP < 2 (PR + QS)`.

View SolutionIn Fig.
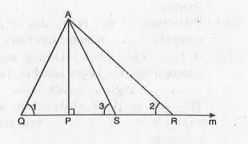 ,
,
AP is the shortest line-segment that can be drawn from A to the line `m`. If `PR > PQ`, prove that `AR > AQ`.
View SolutionIf two sides of a triangle are unequal, then larger side has a smaller angle opposite to it.
View SolutionIf two angles of a triangle are unequal, then greater angle has the larger side opposite to it,
View SolutionSum of any two sides of a triangle is greater than the third side.
View SolutionDifference of any two sides of a triangle is equal to the third side.
View SolutionOf all the line-segments that can be drawn from a point to a line not containing it, the perpendicular line-segment is the shortest.
View SolutionSum of the three sides of a triangle is less than the sum of its three altitudes.
View SolutionSum of any two sides of a triangle is ........... than the third side.
View SolutionIf two angles of a triangle are unequal, then smaller angle has the ............ side opposite to it.
View SolutionOf all line-segments drawn from a point to a line not containing it the ............... line-segment is the shortest.
View SolutionDifference of any two sides of a triangle is ...... Than third side.
View SolutionIf two sides of a triangle are unequal, then the larger side has the ................. angle opposite to it.
View SolutionThe sum of three altitudes of a triangle is ........... Than its perimeter.
View SolutionIn a right-triangle, the hypotenuse is the .......... side.
View SolutionThe perimeter of a triangle is ................... than the sum of its medians.
View SolutionABC is a triangle. Locate a point in the interior of `DeltaABC` which is equidistant from all the vertices of `DeltaABC`.
View SolutionIn a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
View SolutionIf n lines are drawn in a plane such that no two of them are parallel and no three of them are concurrent, then find number of different points at which these lines will cut.
View SolutionComplete the hexagonal rangoli and the star Rangolies (see Figs.
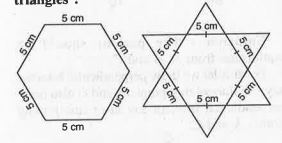 ) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles ?
) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles ?
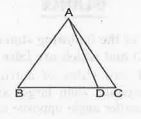
View SolutionIn quadrilateral ABCD AC = AD and AB bisects `angleA` (see fig.
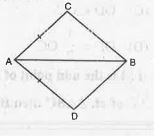 ) `DeltaABC ~= DeltaABD`. What is the relation between BC and BD ?
) `DeltaABC ~= DeltaABD`. What is the relation between BC and BD ?
View SolutionABCD is a quadrilateral in which AD = BC and `angleDAB = angleCBA`. If `DeltaABD ~= DeltaBAC` what is the relation between `angleABD` and `angleBAC` ?
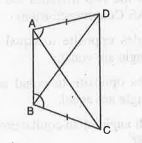
View SolutionAD and BC are equal perpendicular to line segment AB. If `DeltaBOC ~= DeltaAOD` what is the relation between OC and OD ?

View SolutionIf M is the mid point of hypotenuse AC of rt. `DeltaABC` then `BM = 1/2.....`
View SolutionIn fig.
 `AB = AC` and `BE = CD`. If `DeltaACD ~= DeltaABE` then `AD=.......
`AB = AC` and `BE = CD`. If `DeltaACD ~= DeltaABE` then `AD=.......
View SolutionABC is a right angled triangle in which `angle A = 90^@` and AB = AC. Find `angle B` and `angle C`.
View SolutionThe measure of each angle of an equilateral triangle is :
View SolutionIf vertical angle of an isosceles triangle is `40^@`. Find the measure of other two angles.
View SolutionIf `angleA, angleB` and `angleC` of `DeltaABC` are equal then triangle is :
View SolutionIn a triangle, the angle opposite to the longer side is :
View SolutionIn a triangle side opposite to larger angle is :
View SolutionIn a triangle, the sum of its two sides is..... third side.
View SolutionIn a triangle, the angle opposite to the longer side is :
View SolutionIn fig.
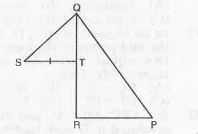 , PQR is a triangle in which T is a point on QR and if S is a point such that RT = ST : then PQ + PR ...... QS
, PQR is a triangle in which T is a point on QR and if S is a point such that RT = ST : then PQ + PR ...... QS
View SolutionThe sum of three altitudes of a triangle is ...... The sum of its three sides.
View SolutionIn a right angled triangle .......... is the longest side.
View SolutionIn fig.
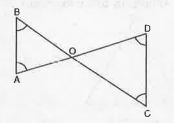 , `angleB < angleA` and `angleC < angleD` then relation between AD and BC is :
, `angleB < angleA` and `angleC < angleD` then relation between AD and BC is :
View SolutionIn `DeltaABC`, If `angleA = angleB= 62frac(1_@) 2` then the longest side is :
View SolutionIn `DeltaABC`, `AC > AB` and bisector of `angleA` meets BC and D then `angleADB` is :
View Solution
Exercise questions and complete solutions for chapter Triangles of MBD of Class 9