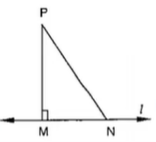
Of all the line segments drawn from a point P to line not containing P, let PD be the shortest. If B and C are points on such that D is the mid-point of BC, prove that PB = PC.Solution in Punjabi
Step by step video & image solution for Of all the line segments drawn from a point P to a line l not containing P, let PD be the shortest. If B and C are points on l such that D is the mid-point of BC, prove that PB = PC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of Rs 10 per m2 is Rs 15000, find the height of the hall.
View SolutionOf all the line segments drawn from a point P to a line m not containing P, let PD be the shortest. If B and C are points on m such that D is the mid-point of BC , prove that PB=PC.
View SolutionOf all the line segments that can be drawn to a given line, from a point, not lying on it, the perpendicular line segment is the shortest. GIVEN : A straight line l and a point P not lying on l. PM⊥l and N is any point on 1 other than M. TO PROVE : PM<PN
View SolutionIf AB,AC,AD, and AE are parallel to a line l, then points A,B,C,D and E are collinear
View SolutionTwo lines which are parallel to the same line, are parallel to each other
View SolutionOf all the lines segments drawn from a point P to a line m not containing P, let PD be the shortest. If B and C are points on m such that D is the mid-point of BC , prove that PB=PC
View Solutionबिंदु P से रेखा l पर डाले गये सभी रेखाखण्डों में PD सबसे छोटा है । यदि रेखा l पर B व C बिंदु इस प्रकार है कि D रेखा BC का मध्य बिंदु है । तब सिद्ध कीजिए कि PB = PC
View Solutionएक बिन्दु P से, जो रेखा m पर स्थित नहीं है, रेखा m तक खींचे गए सभी रेखाख़ण्डों में से माना PD सबसे छोटा है | यदि m पर B और C ऐसे बिन्दु हैं कि D,BC का मध्य-बिन्दु करो कि PB=PC.
View SolutionD is the mid-point of the side BC of the ΔABC and P is any point on BC. Let us join P, A. The line segment drawn through D, parallel to PA intersects AB at Q. Prove that ΔBPQ=12ΔABC.
View SolutionOf all the line segments drawn from a point P to a line m not containing P, let PD be the shortest. If B and C are points on m such that D is the mid-point of BC , prove that PB=PC.
View SolutionIn Figure, lIIm and M is the mid-point of the line segment AB. Prove that M is also the mid-point of any line segment CD having its end-points on l and m respectively.
View SolutionOf all the line segments that can be drawn to a given line, from a point, not lying on it, the perpendicular line segment is the shortest. GIVEN : A straight line l and a point P not lying on l. PM⊥l and N is any point on 1 other than M. TO PROVE : PM<PN
View SolutionIn Figure, l∣∣m and M is the mid-point of the line segment AB . Prove that M is also the mid-pooint of any line segment CD having its end-points on l and m respectively.
View SolutionOf all the lines segments drawn from a point P to a line m not containing P, let PD be the shortest. If B and C are points on m such that D is the mid-point of BC , prove that PB=PC .
View SolutionOf all the line segments drawn from a point P to a line l not containing P, let PD be the shortest. If B and C are points on l such that D is the mid-point of BC, prove that PB = PC.
View SolutionAB ਇਕ ਰੇਖਾ ਖੰਡ ਹੈ ਅਤੇ ਰੇਖਾ l ਇਸ ਦਾ ਲੰਬ ਸਮਦੁਭਾਜਕ ਹੈ। ਜੇਕਰ ਬਿੰਦੂ P,l ਉੱਤੇ ਹੋਵੇ ਤਾਂ ਸਿਧ ਕਰੋ ਕਿ P ਬਿੰਦੂ A ਅਤੇ B ਤੋਂ ਬਰਾਬਰ ਦੂਰੀ ਉੱਤੇ ਹੈ।
View Solution
