Complete Solutions to Exercise of chapter Quadrilaterals of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | Quadrilaterals |
| MBD | Exercise |
| Number Of Questions | 92 |
| Academic Year | 2023-24 |
If diagonals of a quadrilateral bisect each other at right angles, then it is a :
View SolutionA quadrilateral is a parallelogram, if its one pair of opposite sides are equal and parallel.
View SolutionThe diagonals of a rectangle are of the equal length.
View SolutionThe diagonals of a rhombus are perpendicular to each other .
View SolutionIf the diagonals of a parallelogram are perpendicular, then it is a rhombus.
View SolutionDiagonal AC of a parallelogram ABCD bisects `/_A` (See fig.)
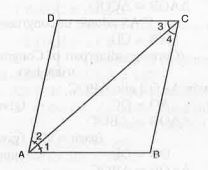 . Show that It bisects `/_C` also.
. Show that It bisects `/_C` also.
View SolutionDiagonal AC of a parallelogram ABCD bisects `/_A` (See fig.)
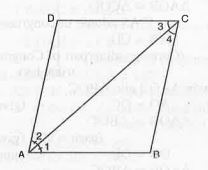 . Show that ABCD is `a` rhombus.
. Show that ABCD is `a` rhombus.
View SolutionABCD is a rhombus. Show that the diagonal AC bisects `/_A` as well as `/_C` and diagonal BD bisects `/_B` as well as `/_D`.
View SolutionABCD is a rectangle in which diagonal AC bisects `/_A as well as `/_C`. Show that ABCD is a square.
View SolutionABCD is a rectangle in which diagonal AC bisects `/_A as well as `/_C`. Show that Diagonal BD bisects both `/_B` as well as `/_D`.
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.
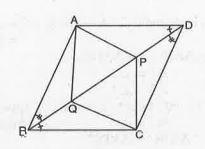 ) Show that `Delta APD ~= Delta CQB`.
) Show that `Delta APD ~= Delta CQB`.
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.
 ) Show that `AQ=CP`.
) Show that `AQ=CP`.
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.
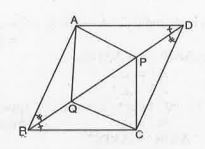 ) Show that `Delta AQB ~= Delta CPD`.
) Show that `Delta AQB ~= Delta CPD`.
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.
 ) Show that `AQ=CP`.
) Show that `AQ=CP`.
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.
 ) Show that APCQ is a parallelogram.
) Show that APCQ is a parallelogram.
View SolutionABCD is a parallelogram and AP and CQ are the perpendiculars from vertices A and C on its diagonal BD (See fig.) Show that `Delta APB ~= Delta CQD`.
View SolutionABCD is a parallelogram and AP and CQ are the perpendiculars from vertices A and C on its diagonal BD (See fig.)
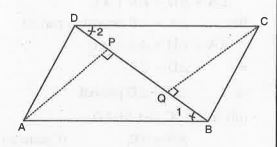 Show that AP = CQ.
Show that AP = CQ.
View SolutionIn `Delta ABC` and `Delta DEF` , AB = DE, `AB|| DE`, BC = EF and `BC|| EF`. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
 Show that quadrilateral ABED is a parallelogram.
Show that quadrilateral ABED is a parallelogram.
View SolutionIn `Delta ABC` and `Delta DEF` , AB = DE, `AB|| DE`, BC = EF and `BC|| EF`. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
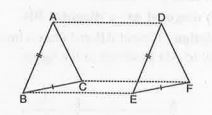 Show that `AD ||CF` and AD=CF.
Show that `AD ||CF` and AD=CF.
View SolutionIn `Delta ABC` and `Delta DEF` , AB = DE, `AB|| DE`, BC = EF and `BC|| EF`. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
 Show that `AD ||CF` and AD=CF.
Show that `AD ||CF` and AD=CF.
View SolutionIn `Delta ABC` and `Delta DEF` , AB = DE, `AB|| DE`, BC = EF and `BC|| EF`. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
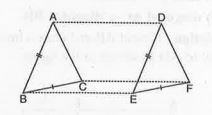 Show that quadrilateral ACFD is a parallelogram.
Show that quadrilateral ACFD is a parallelogram.
View SolutionIn `Delta ABC` and `Delta DEF` , AB = DE, `AB|| DE`, BC = EF and `BC|| EF`. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
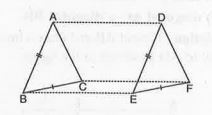 Show that AC=DF.
Show that AC=DF.
View SolutionIn `Delta ABC` and `Delta DEF` , AB = DE, `AB|| DE`, BC = EF and `BC|| EF`. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
 Show that `DeltaABC ~= DeltaDEF`.
Show that `DeltaABC ~= DeltaDEF`.
View SolutionABCD is a trapezium in which `AB||CD` and AD = BC (See Fig.)
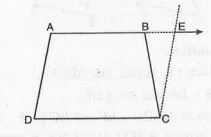 Show that `/_A = /_B`.
Show that `/_A = /_B`.
View SolutionFind x+y+z
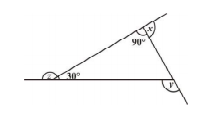
View SolutionFind x+y+z

View SolutionABCD is a trapezium in which `AB||CD` and AD = BC (See Fig.)
 Show that diagonal AC = diagonal BD.
Show that diagonal AC = diagonal BD.
View SolutionIn a parallelogram ABCD, `/_D = 115^@`, determine the measure of `/_A and `/_B`.
View SolutionIn Fig.
 ABCD is a parallelogram, compute the values of x and y.
ABCD is a parallelogram, compute the values of x and y.
View SolutionIn Fig. find the four angles A, B, C and D in the parallelogram ABCD.
View SolutionIn a parallelogram ABCD, diagonals AC and BD intersect at O and AC = 6.8 cm and BD = 5.6 cm. Find the measure of OC and OD.
View SolutionIn a parallelogram ABCD, the bisector of `/_A` also bisects BC at X. Prove that AD = 2AB.
View SolutionABCD is a parallelogram. AB is produced to E, so that BE = AB. Prove that ED bisects BC.
View SolutionFind the measure of all the angles of a parallelogram, if one angle is `24^@` less than twice of the smallest angle.
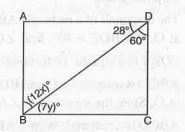
View SolutionIn Fig.
 ABCD is a parallelogram in which `/_DAB = 75^@` and `/_DBC = 60^@`. Compute `/_CDB` and `/_ADB`.
ABCD is a parallelogram in which `/_DAB = 75^@` and `/_DBC = 60^@`. Compute `/_CDB` and `/_ADB`.
View SolutionIn Fig. .
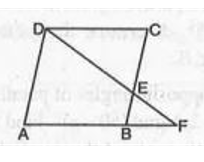
ABCD is a parallelogram and E is the mid-point of side BC. If DE and AB, when produced meet at F, prove that AF = 2AB.
View SolutionIn a parallelogram, prove that sum of any two consecutive angles is `180^@`.
View SolutionIf ABCD is a quad, in which `AB || CD` and AD = BC. Prove that `/_A = /_B`.
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL = CM. Prove that LM and BD bisect each other.
View SolutionIn Fig.
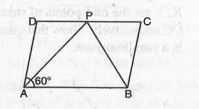 ABCD is a parallelogram in which `/_A = 60^@`. If the bisector of `/_A` and `/_B` meet at P prove that AD = DP, PC = BC and AC = 2AD.
ABCD is a parallelogram in which `/_A = 60^@`. If the bisector of `/_A` and `/_B` meet at P prove that AD = DP, PC = BC and AC = 2AD.
View SolutionPQRS is a parallelogram. PX and QY are respectively, the perpendiculars from P and Q to SR and RS produced. Prove that PX = QY.
View SolutionThe line drawn through the mid-points of one side of a triangle, parallel to another side, intersects the third side at its midpoint.
View SolutionIf there are three parallel lines, and the intercepts made by them on one transversal are equal, then the intercepts on any other transversal are also equal.
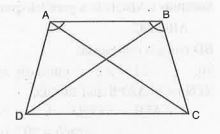
View SolutionABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See Fig.
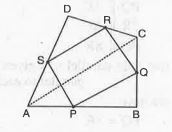 AC is a diagonal Show that `SR II AC and SR = 1/2 AC`.
AC is a diagonal Show that `SR II AC and SR = 1/2 AC`.
View SolutionABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See Fig.)
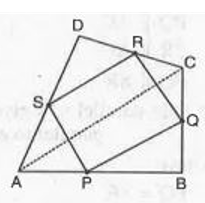 AC is a diagonal Show that PQ = SR.
AC is a diagonal Show that PQ = SR.
View SolutionABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See Fig.)
 AC is a diagonal Show that PQRS is a parallelogram.
AC is a diagonal Show that PQRS is a parallelogram.
View SolutionABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD and DA respectively. Prove that quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
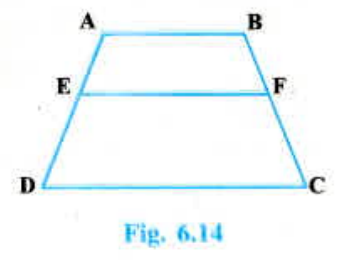
View SolutionABCD is a trapezium with AB II DC, E and F are paints on non-parallel sides AD and BC respectively such that EF is parallel to AB Show that `(AE)/(ED)=(BF)/(FC)`.
View SolutionMatch the following :
 .
.
View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisect each other.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that D is the mid-point of AC.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that `MD _|_ AC`.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that CM = MA = `1/2 AB` .
View SolutionProve that the figure formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View SolutionIn a triangle, P, Q and R are mid-points of sides BC, CA and AB respectively. If AC = 21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
View SolutionIn a `DeltaABC` median AD is produced to X such that AD = DX. Prove that ABXC is a parallelogram.
View SolutionIn Fig.
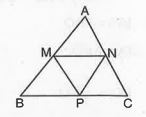 M, N and P are the mid-points of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5 cm, and MP = 2.5 cm, calculate BC and AB and AC.
M, N and P are the mid-points of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5 cm, and MP = 2.5 cm, calculate BC and AB and AC.
View SolutionABCD is a trapezium in which `AB || DC`. M and N are the mid-points of AD and BC respectively. If AB = 12 cm, and MN = 14 cm, find CD.
View SolutionIn Fig.
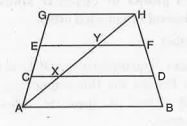 , `AB || CD || EF || GH` and AX = XY=YH. If AC = 1.5 cm., find AG.
, `AB || CD || EF || GH` and AX = XY=YH. If AC = 1.5 cm., find AG.
View SolutionIn given Fig.
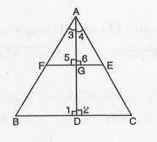 ,
,
`DeltaABC` is isosceles with AB = AC. D, E, F are the mid-points of sides BC, AC and AB respectively. Show that the line segment AD is perpendicular to the line segment EF and is bisected by it.
View SolutionIn `DeltaABC`, E and F are the mid-points of AC and AB respectively. The altitude AP to BC intersects FE at Q. Prove that AQ = QP.
View SolutionIn Fig.
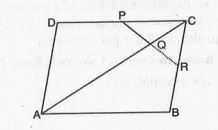 ,
,
ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that `CQ = 1/4AC`. If PQ produced meets BC at R, prove that R is a mid-point of BC.
View SolutionABCD is a parallelogram. P is any point on AD, such that `AP = 1/3AD` and Q is a point on BC such that `CQ = 1/3AD` . Prove that AQCP is a parallelogram.
View SolutionIn Fig.
 ,
,
ABCD is a trapezium in which `AB || DC` and P, Q are mid-points of AD and BC respectively. If CP and BA when produced meet at E, prove that `PQ ||DC`.
View SolutionIn Fig.
 ,
,
ABCD is a trapezium in which `AB || DC` and P, Q are mid-points of AD and BC respectively. If CP and BA when produced meet at E, prove that `PQ ||DC`.
View SolutionIn Fig.
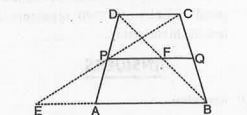 ,
,
ABCD is a trapezium in which `AB || DC` and P, Q are mid-points of AD and BC respectively. If CP and BA when produced meet at E, prove that `PQ=1/2(AB+DC)`.
View SolutionWhat is the value of `sina` .
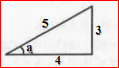 .
.
View SolutionThe triangle formed by joining the midpoints of the sides of an isosceles triangle is ................ .
View SolutionThe triangle formed by joining the midpoints of the sides of a right triangle is ............... .
View SolutionThe figure formed by joining the midpoints of the consecutive sides of a quadrilateral is ............... .
View SolutionIf a line is divided by three parallel lines into two segments of lengths in the ratio `1 : 3` another line will be divided by these parallel lines into two segments of lengths in the ratio .............. .
View SolutionThe bisectors of angles of a parallelogram from a :
View SolutionThe angles of a quadrilateral are in the ratio `3 : 4 : 5 : 6`. The respective angles of the quadrilateral are :
View SolutionIf diagonals of a quadrilateral bisect each other at right angles, then it is a :
View SolutionIf in rectangle ABCD
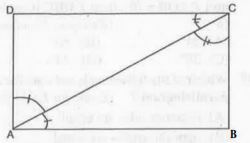 , diagonal AC bisects `/_A` as well as `/_C` , then ABCD is a :
, diagonal AC bisects `/_A` as well as `/_C` , then ABCD is a :
View SolutionThe line-segment joining the mid-points of two sides of a triangle is parallel to the third side and ............. Of it.
View SolutionLine segment joining the mid-points of the opposite sides of a quadrilateral ............. each other.
View SolutionThree angles of a quadrilateral are `75^@, 90^@` and `75^@`. The fourth angle is
View SolutionA diagonal of a rectangle is inclined to one side of the rectangle at `25^@`. The acute angle between the diagonals is
View SolutionABCD is a rhombus such that `/_ACB = 40^@`. Then `/_ADB` is
View SolutionThe quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if
View SolutionThe quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rhombus, if
View SolutionIf angles A, B, C and D of the quadrilateral ABCD, taken in order, are in the ratio `3:7:6:4`, then ABCD is
View SolutionIf bisectors of `/_A` and `/_B` of a quadrilateral ABCD intersect each other at P, of `/_B` and `/_C` at Q, of `/_C` and `/_D` at R and of `/_D` and `/_A` at S, then PQRS is a
View SolutionIf APB and CQD are two parallel lines, then the bisectors of the angles APQ, BPQ, CQP and PQD form
View SolutionThe figure obtained by joining the midpoints of the sides of a rhombus, taken in order, is
View SolutionDand E are the mid-points of the sides AB and AC of `DeltaABC` and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is
View SolutionThe figure formed by joining the midpoints of the sides of a quadrilateral ABCD, taken in order, is a square only
View SolutionThe diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If `/_DAC = 32^@` and `/_AOB=70^@`, then `/_DBC` is equal to
View SolutionWhich of the following is not true for a parallelogram?
View SolutionD and E are the mid-points of the sides AB and AC respectively of `DeltaABC`. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is
View Solution
Exercise questions and complete solutions for chapter Quadrilaterals of MBD of Class 9