In Fig.
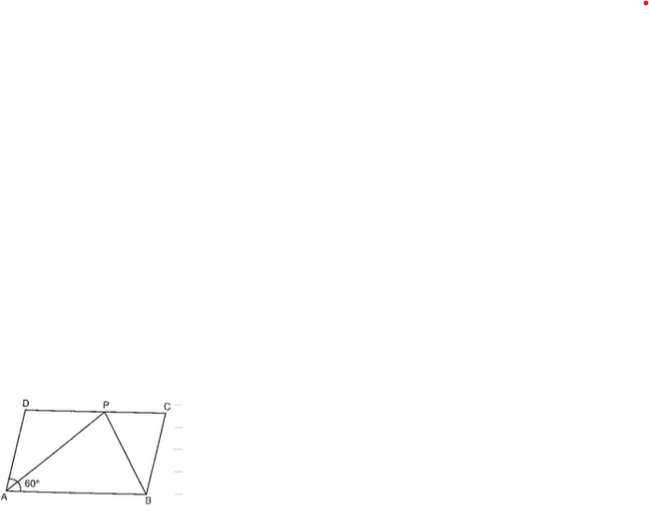
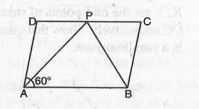 ABCD is a parallelogram in which ∠A=60∘. If the bisector of ∠A and ∠B meet at P prove that AD = DP, PC = BC and AC = 2AD.Solution in Punjabi
ABCD is a parallelogram in which ∠A=60∘. If the bisector of ∠A and ∠B meet at P prove that AD = DP, PC = BC and AC = 2AD.Solution in Punjabi
Step by step video & image solution for In Fig. ABCD is a parallelogram in which /_A = 60^@. If the bisector of /_A and /_B meet at P prove that AD = DP, PC = BC and AC = 2AD. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A coin is tossed 1000 times with the following frequencies of head and tail head : 455, tail : 545 compute the experimental probability for each type of outcome, i.e. head and tail.
View SolutionThe weights (in kg) of 30 students of a class are 49, 48, 46, 48, 48, 50, 52, 53, 54, 43, 43, 41, 43, 55, 56, 48, 47, 41, 40, 49, 51, 51, 56, 46, 45, 44, 49, 53, 42 and 47. Prepare a frequency table for the above data and answer the following questions : What is the least weight ?
View SolutionIn Figure, ABCD is a parallelogram in which ∠A=600 . If the bisectors of ∠A and ∠B meet at P, prove that AD=DP,PC=BC and DC=2AD.
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionDraw the bisector of ∠AOB=58∘
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_VII_C05_S01_009_Q01.png" width="80%"gt
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionIn Fig, find the value of x.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_S01_032_Q01.png" width="80%"gt
View SolutionAt point P, the value of (dy)/(dx) is : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_025_Q01.png" width="80%"gt
View Solution
