ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that CM = MA = 12AB .Solution in Punjabi
Step by step video & image solution for ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that CM = MA = 1/2 AB . by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A coin is tossed 1000 times with the following frequencies of head and tail head : 455, tail : 545 compute the experimental probability for each type of outcome, i.e. head and tail.
View SolutionThe weights (in kg) of 30 students of a class are 49, 48, 46, 48, 48, 50, 52, 53, 54, 43, 43, 41, 43, 55, 56, 48, 47, 41, 40, 49, 51, 51, 56, 46, 45, 44, 49, 53, 42 and 47. Prepare a frequency table for the above data and answer the following questions : What is the least weight ?
View SolutionABC is a triangle right-angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD⊥AC
(iii) CM = MA=12AB
View SolutionABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य - बिंदु M से होकर BC के समांतर खींची गई रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि
(i) D भुजा AC का मध्य - बिंदु है। (ii ) MD⊥AC है
(iii) CM=MA=12AB है।
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
D is the mid-point of AC
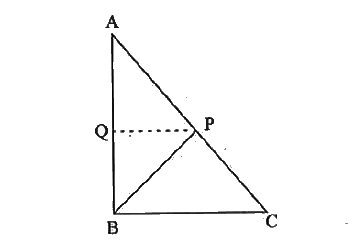
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
MD⊥AC
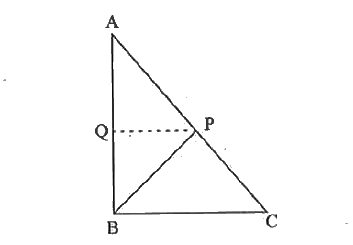
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
CM=MA=12AB

View SolutionABC is a triangle right angled at C. A line through the mid points M of hypotenuse AB and parallel to BC intersects AC at D. Show that
D is the mid point of AC
MD⊥AC
CM=MA=12AB
View SolutionABC is a right angle in a right triangle ABC. If the line drawn parallel to BC through the hypotenuse AB denominator M intersects AC at D, then prove the following point AC midpoint D
View SolutionABC is a right angle in a right triangle ABC. Prove the following if the line drawn parallel to BC through the midpoint M of hypotenuse AB intersects AC at D. CM=MA = 1/2 AB
View SolutionABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and Parallel to BC intersects AC at D. Show that
(i) D is the midpoint of AC
(ii) MD⊥AC
(iii) CM=MA=12AB.
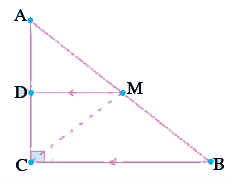
View SolutionABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and Parallel to BC intersects AC at D. Show that
(i) D is the midpoint of AC
(ii) MD⊥AC
(iii) CM=MA=12AB.
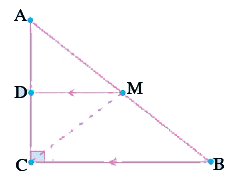
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that (i) D is the mid-point of AC (ii) MD⊥AC (iii) CM=MA=12AB
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that D is the mid-point of AC.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that MD⊥AC.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that CM = MA = 12AB .
View Solution
