Complete Solutions to Solved Examples of chapter AREA OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREA OF PARALLELOGRAMS AND TRIANGLES |
| NAGEEN PRAKASHAN | Solved Examples |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
The area of a parallelogram is `32 cm^(2)`. If its altitude is twice of its base, then find its base and the altitude
View SolutionThe area of a parallelogram is `150cm^(2)`. If the ratio of its base and corresponding altitude is `3 : 2`, find the length of base and altitude
View SolutionThe diagonals of a parallelogram `A B C D` intersect at `Odot` A line through `O` meets `A B\ ` in `x\ a n d\ C D` in `Ydot` Show that `a r\ (A X Y X)=1/2(a r|""|^(gm)\ \ A B C D)`
View SolutionShow that a median of a triangle divides it into two triangles of equal areas.
View SolutionIn quadrilateral ABCD, diagonal BD is bisected by the diagonal AC. Prove that : `Delta ABC and Delta ADC` are equal in area.
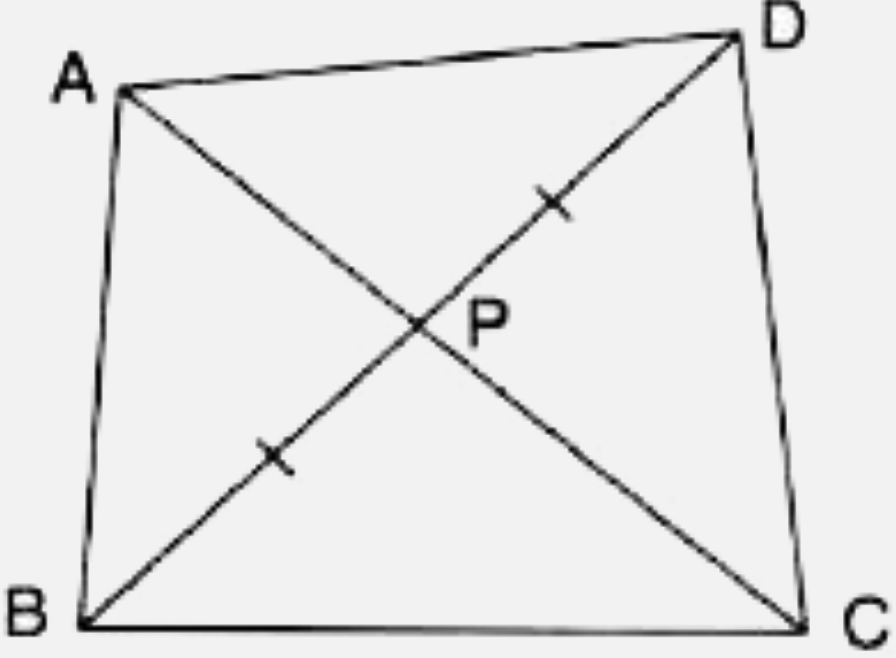
View SolutionIf each diagonals of a quadrilateral separates it into two triangles of equal area then show that the quadrilateral is a parallelogram.
View SolutionA point `O` inside a rectangle `A B C D` is joined to the vertices. Prove that the sum of the areas of a pair of opposite triangles so formed is equal to the sum of the areas of other pair of triangles.
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of `Delta ABC`. Prove that:
(i) `square BDEF` is a parallelogram
(ii) area of `Delta DEF = (1)/(4) xx " area of " Delta ABC`
(iii) `square BDEF = (1)/(2) xx " area of " Delta ABC`

View SolutionIn the adjoining figure, AD is the median of `Delta ABC` and X be any point on side AD. Prove that:
area `(Delta ABX) = " area " (Delta ACX)`

View SolutionThe medians of `Delta ABC` intersect at point G. Prove that:
area of `Delta AGB = (1)/(3) xx " area of " Delta ABC`
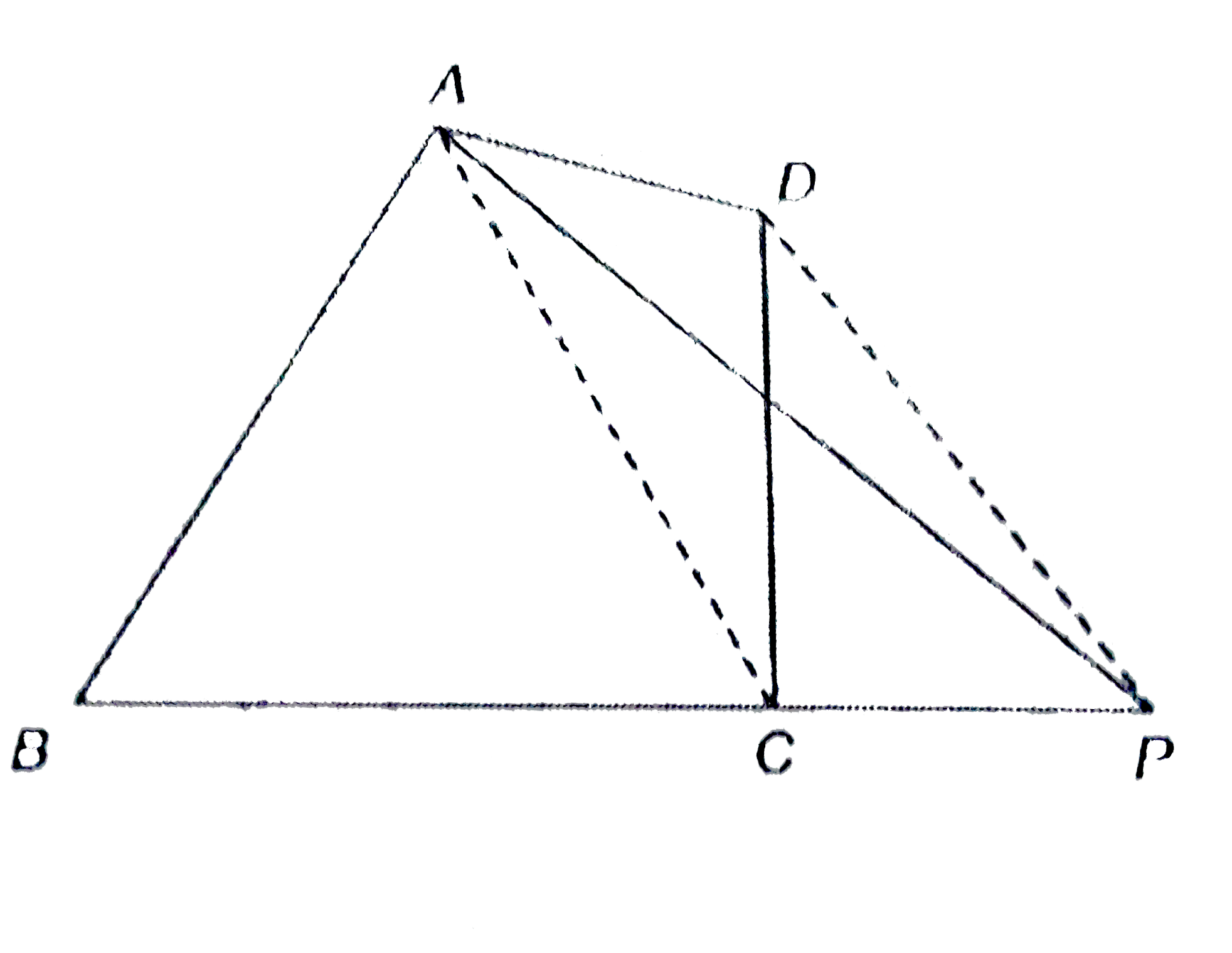
View SolutionIn the figure, ABCD is a quadrilateral. A line DP drawn parallel to diagonal AC from point D, meet BC produced at P. Prove that:
are of `Delta ABP = " area of " square ABCD`
View Solution`XY` is a line parallel to side `BC` of a triangle `ABC`. If `B E ||A C` and `C F\ ||\ A B` meet `XY` at `E` and `F` respectively, show that `a r\ (A B E)\ =\ a r\ (A C F)`
View SolutionA point `D` is taken on the side `B C` of a ` A B C` such that `B D=2d Cdot` Prove that `a r( A B D)=2a r( A D C)dot`
View Solution`XY` is a line parallel to side `BC` of a triangle `ABC`. If `B E ||A C` and `C F\ ||\ A B` meet `XY` at `E` and `F` respectively, show that `a r\ (A B E)\ =\ a r\ (A C F)`
View SolutionIn the figure, ABC and BDE are two equilateral triangle such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) `ar(DeltaBDE) = (1)/(4) ar(DeltaABC)` (ii) `ar(DeltaBDE) = (1)/(2) ar(DeltaBAE)`
(iii) `ar(DeltaABC) = 2 ar(DeltaBEC)` (iv) `ar(DeltaBFE) = ar(DeltaAFD)`
(v) `ar(DeltaBFE) = 2ar(DeltaFED)` (vi) `ar(DeltaFED) = (1)/(8) ar(DeltaAFC)`

View Solution`A B C D` is a parallelogram `X` and `Y` are the mid-points of `B C` and `C D` respectively. Prove that `a r( A X Y)=3/8a r(^(gm)A B C D)`
View Solution
Solved Examples questions and complete solutions for chapter AREA OF PARALLELOGRAMS AND TRIANGLES of NAGEEN PRAKASHAN ENGLISH of Class 9