Complete Solutions to Exercise of chapter AREA OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREA OF PARALLELOGRAMS AND TRIANGLES |
| NAGEEN PRAKASHAN | Exercise |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
The base of a parallelogram is 3 times of its corresponding height. If the area of the parallelogram is `48 cm^(2)`, then find the base and the corresponding height of the parallelogram.
View SolutionThe ratio of the base and corresponding height of a parallelogram is `5 : 2`. If the area of the parallelogram is `90 cm^(2)`, then find its base and the corresponding height.
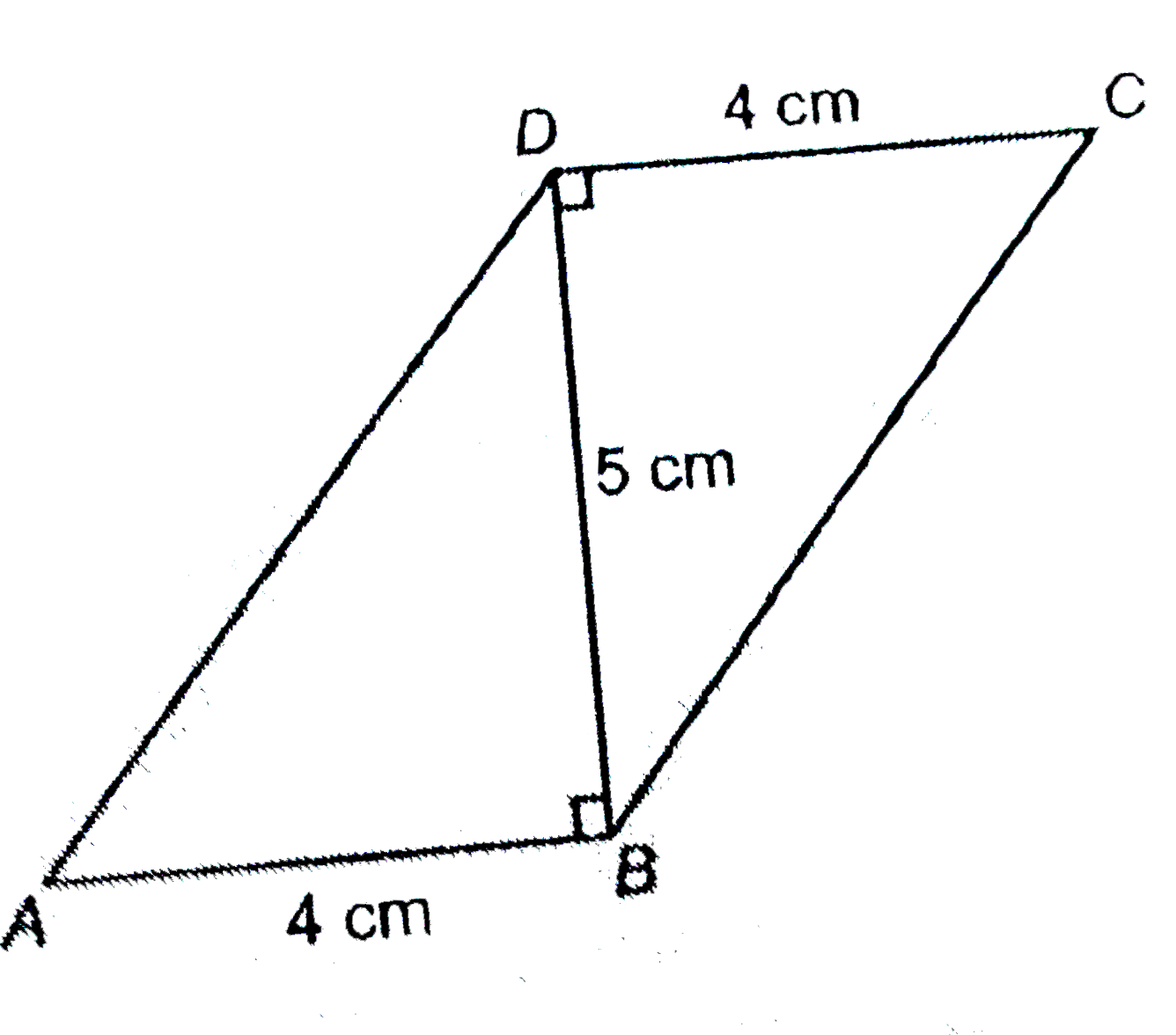
View SolutionIn the adjoining figure, prove that ABCD is a parallelogram. Also find its area.
View SolutionIn the figure, find the length of RN.

View SolutionShow that the segment joining the mid-points of a pair of opposite sides of a parallelogram, divides it into two equal parallelograms.
View SolutionProve that of all parallelograms of which the sides are given, the parallelogram which is rectangle has the greatest area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionIf the diagonals `A C ,\ B D` of a quadrilateral `A B C D ,` intersect at `O ,` and separate the quadrilateral into four triangles of equal area, show that quadrilateral `A B C D` is a parallelogram.
View SolutionThe diagonal AC of a quadrilateral ABCD divides it into two triangles of equal areas. Prove that diagonal AC bisects the diagonal BD.
View SolutionProve that the area of a rhombus is equal to half the rectangle contained by its diagonals. Given: A rhombus `A B C D` such that its diagonals `A C\ a n d\ B D` intersect at `Odot` To Prove: `a r\ (r hom b u s\ A B C D)=1/2` (area of the rectangle contained by its diagonals `=1/2(A C\ x\ B D)`
View Solution`Delta ABC and Delta DBC` are on same base BC and their vertices A and D are on opposite sides of BC. It is given that:
area of `Delta ABC = " area of " Delta DBC`
Prove that BC bisects the line segment AD.
View SolutionO' is an interior point of a parallelogram ABCD. Prove that :
area of `Delta AOB + " area of " Delta COD = " area of " Delta AOD + " area of " Delta BOC`
View SolutionO' is any point on diagonal AC of a parallelogram ABCD. Prove that :
area of `Delta AOD = " area of " Delta AOB`
View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of `Delta ABC` and area of `Delta BCE = " area of " Delta BCD`.
Prove that `DE ||BC`

View SolutionIn the adjoning figure, ABCD is a parallelogram. Prove that : area of `Delta BPC = " area of " Delta DPQ`

View SolutionIn a quadrilateral ABCD, AM and CN are perpendiculars from the vertices A and C respectively on diagonal BD. Prove that:
area of `square ABCD = (1)/(2) xx BD xx (AM + CN)`
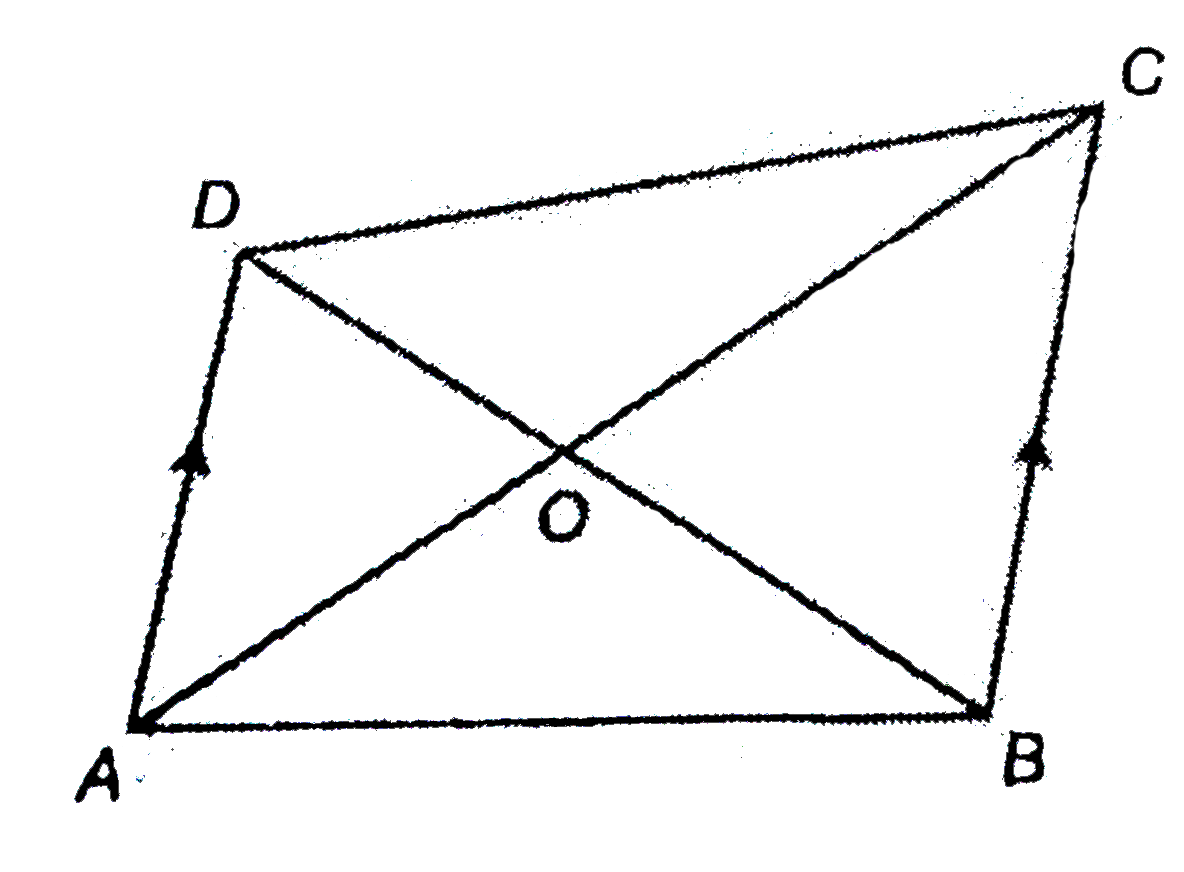
View SolutionIn the adjoining figure, ABCD is a quadrilateral in which `AD ||BC`. AC and BD intersect each other at point 'O'. Prove that:
area of `Delta COD = " area of " Delta ABO`
View SolutionAny point D is taken on the side BC of a ` Delta ABC ` and AD is produced to E such that AD = DE , prove that area of `Delta BCE = ` area of `Delta ABC`,
View SolutionIn the adjoining figure, D is the mid-point of side AB of `Delta ABC` and P be any point on side BC. If `CQ ||PD`, then prove that:
area of `Delta BPQ = (1)/(2) xx " area of " Delta ABC`

View SolutionIn a ` A B C ,\ E` is the mid-point of median `A Ddot` Show that `a r\ ( B E D)=1/4a r\ ( A B C)`
View SolutionIn parallelogram ABCD, P is a point on side AB and Q is a ponit on side BC.
Prove that :
(i) `DeltaCPD` and `DeltaAQD` are equal in area.
(ii) Area `(DeltaAQD)`
`= "Area" (DeltaAPD)+ "Area" (DeltaCPB)`
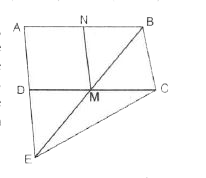
View SolutionIn the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
If the area of parallelogram ABCD is `48cm^(2)`,
(i) State the area of the triangle BEC.
(ii) name the parallelofram which is equal in area to the triangle BEC.
View SolutionABCD and BCFE are parallelograms. If area of triangle `EBC=480cm^(2), AB=30cm "and" BC=40cm`, Calculate,
(i) area of parallelogram ABCD,
(ii) area of the parallelogram BCFE,
(iii) length of altitude from A on CD,
(iv) area of triangle ECF.
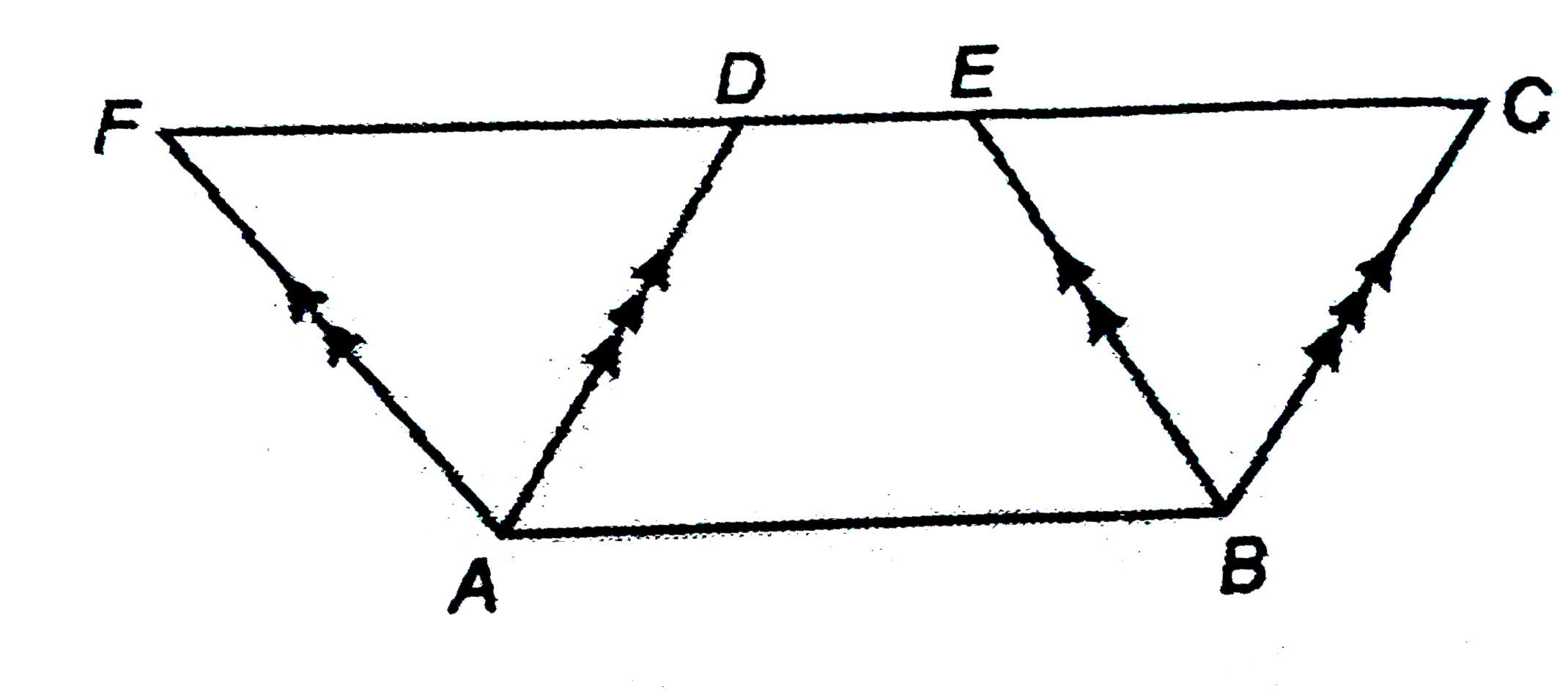
View SolutionThe given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF drawn parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
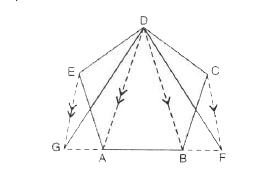
View SolutionIn the given figure, AP is parallel to BC, BP is parallel to CQ. Prove that the areas of triangles ABC and BQP are equal.
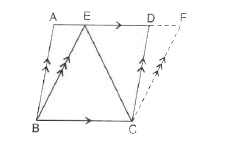
View SolutionThe following figure shows two paralelograms ABCD and ABEF prove that
area of `DeltaADF = " area of DeltaBCE`
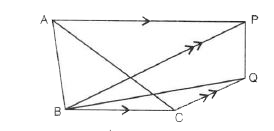
View SolutionThe side `A B` of a parallelogram `A B C D` is produced to any point `Pdot` A line through `A` and parallel to `C P` meets `C B` produced at `Q` and then parallelogram `P B Q R` is completed as shown in Figure. Show that `a r(|"|"hatgm\ A B C D)=a r\ (|""|^(gm)P B Q R)`
View SolutionA point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that `ar(DeltaADF) = ar (ABFC)`.
View SolutionIn the following figure, `AC||PS||QR and PQ||DB||SR`, prove that area of quadrilateral `PQRS = 2 xx` area of quadrilateral ABCD

View Solution`O` is any point on the diagonal `B D` of the parallelogram `A B C D`. Prove that `a r( /_\O A B)=a r( /_\O B C)`
View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that `8 xx " area of " (DeltaAFD) = " area of " Delta ABC`
View SolutionIn `triangleABC`,E and F are mid-points od sides AB and AC respectively. If BF and CE intersect each other at point O, prove that the `DeltaOBC` and quadrilateral AEOF are equal in area.
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= `(1)/(8)` of the area of parallelogram ABCD.
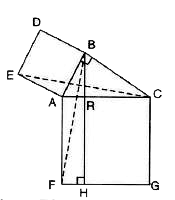
View SolutionIn the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
If BH perpendicular to FG, prove that :
(i) `DeltaEAC~=DeltaBAF`.
(ii) Area of the square ABDE
= Area of the rectangle ARHF.
View Solution
Exercise questions and complete solutions for chapter AREA OF PARALLELOGRAMS AND TRIANGLES of NAGEEN PRAKASHAN ENGLISH of Class 9