Complete Solutions to प्रश्नावली 9.4 of chapter समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल |
| MADHUR GUPTA | प्रश्नावली 9.4 |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
समान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित है और उनके क्षेत्रफल बराबर है। दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाप आयत के परिमाप से अधिक है।
View Solutionआकृति में, भुजा BC पर दो बिन्दु D और E इस प्रकार स्थित है कि BD = DE = EC है। दर्शाइए कि ar(ABD) = ar(ADE) = ar(AEC) है।
क्या आप अब उस प्रश्न का उत्तर दे सकते है, जो आपने इस अध्याय की 'भूमिका' में छोड़ दिया था कि ''क्या बुधिया का खेत वास्तव में बराबर क्षेत्रफलों वाले तीन भागो में विभाजित हो गया है?''

टिप्पणी : ध्यान दीजिए कि BD = DE = EC लेने से `DeltaABC` तीन त्रिभुजों ABD, ADE और AEC में विभाजित हो जाता है जिनके क्षेत्रफल बराबर है। इस प्रकार, BC को n बराबर भागो में विभाजित करके और इस भुजा को विभाजित करने वाले बिन्दुओं को सम्मुख शीर्ष A से मिलकर आप इस त्रिभुज को बराबर क्षेत्रफलों वाले n त्रिभुजों में विभाजित कर सकते है।
View Solutionआकृति में ABCD, DCFE और ABFE समान्तर चतुर्भुज है। दर्शाइए कि ar(ADE) = ar(BCF) है।
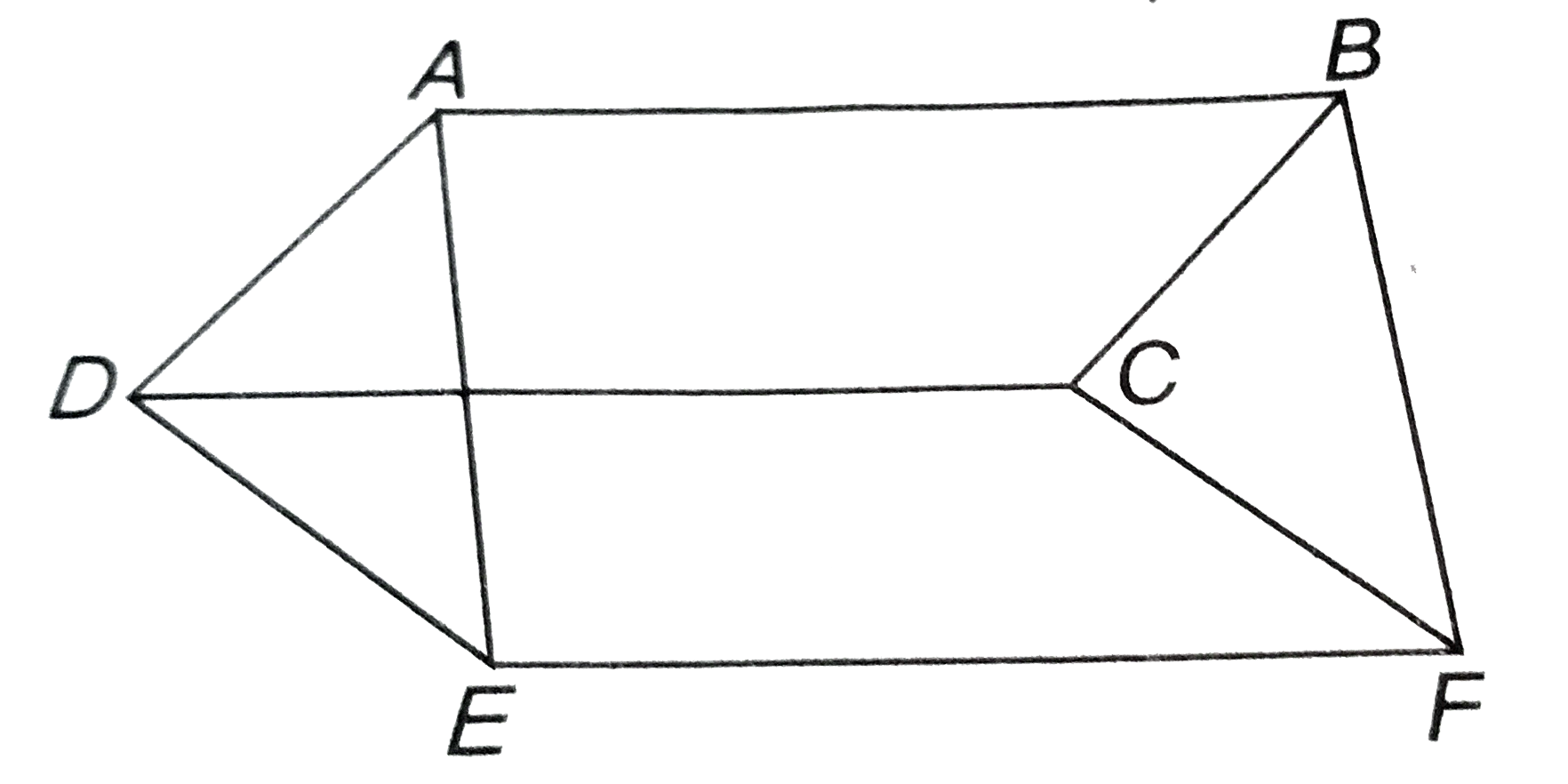
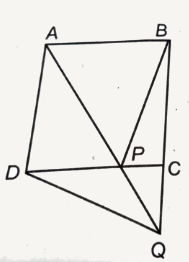
View Solutionआकृति में, ABCD एक समान्तर चतुर्भुज है और BC को एक बिन्दु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ भुजा DC को P पर प्रतिच्छेद करती है, तो दर्शाइए कि ar(BPC) = ar(DPQ) है।
संकेत : AC को मिलाइए
View Solutionआकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार है कि D भुजा BC का मध्य-बिन्दु है। यदि AE भुजा BC को F पर प्रतिच्छेद करती है, तो दर्शाइए कि
(i)`ar(DeltaBDE)=(1)/(4)ar(DeltaABC)`
(ii) `ar(DeltaBDE)=(1)/(2)ar(DeltaBAE)`
(iii) `ar(DeltaABC)=2ar(DeltaBEC)`
(iv) `ar(DeltaBFE)=ar(DeltaAFD)`
(v) `ar(DeltaBFE)=2ar(DeltaFED)`
(vi) `ar(DeltaFED)=(1)/(8)ar(DeltaAFC)`
संकेत : EC और AD को मिलाइए। दर्शाइए कि `"BE || AC"` और `"DE || AB"` है, इत्यादि।

View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते है। दर्शाइए कि `ar(APB)xxar(CPD)=ar(APD)xxar(BPC)` है।
संकेत : A और C से BD पर लम्ब खींचिए
View SolutionP और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिन्दु है तथा R रेखाखण्ड AP का मध्य-बिन्दु है। दर्शाइए कि :
(i) `ar(PRQ)=(1)/(2)ar(ARC)`
(ii) `ar(RQC)=(3)/(8)ar(ABC)`
(iii) `ar(PBQ)=ar(ARC)`
View Solutionआकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग है। रेखाखण्ड `AX_|_DE` भुजा BC को बिन्दु Y पर मिलता है। दर्शाइए कि :
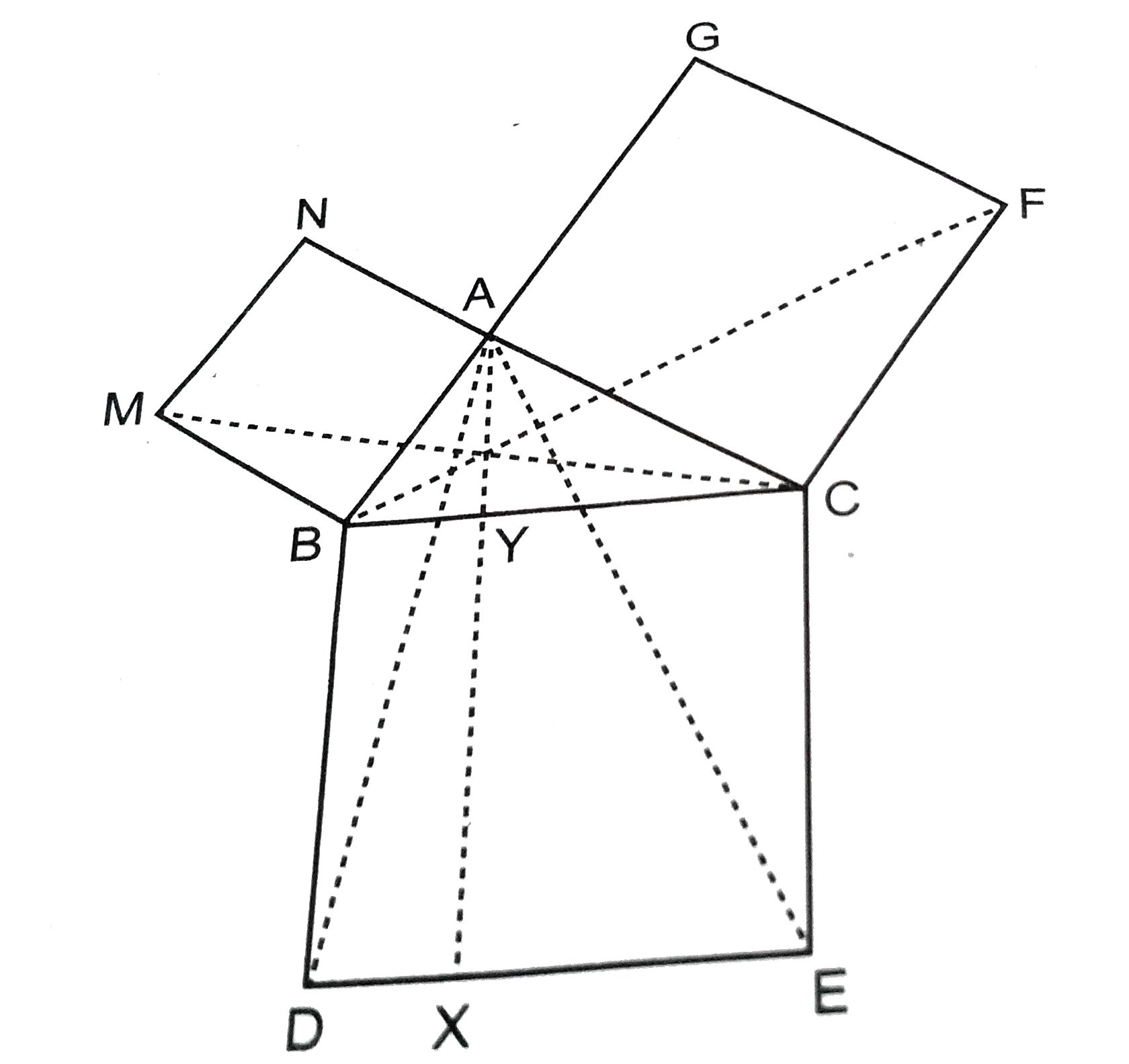
(i) `DeltaMBC ~= DeltaABD`
(ii) `ar(BYXD) = 2 ar (MBC)`
(iii) ar(BYXD) = ar(AMBN)
(iv) `DeltaFCB~=DeltaACE`
(v) ar(CYXE)=2ar(FCB)
(vi) ar(CYXE)=ar(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACEG)
टिप्पणी : परिणाम (vii) प्रसिद्ध, (सुपरिचित) पाइथागोरस प्रमेय है। इस प्रमेय की एक सरलतम उपपत्ति आप कक्षा X में पढ़ेंगे।
View Solution
प्रश्नावली 9.4 questions and complete solutions for chapter समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of NAGEEN MATHS (HINDI) of Class 9