P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिन्दु है तथा R रेखाखण्ड AP का मध्य-बिन्दु है। दर्शाइए कि :
(i) ar(PRQ)=12ar(ARC)
(ii) ar(RQC)=38ar(ABC)
(iii) ar(PBQ)=ar(ARC)
(i) प्रश्नानुसार ΔABC में बिन्दु P तथा Q क्रमशः भुजाओं AB और BC के मध्य-बिन्दु है। AQ तथा PC को मिलाया ΔAPQ की माध्यिका QR है।

अतः ar(ΔPRQ)=12ar(ΔAPQ) …(1)
पुनः ΔABQ की माध्यिका QP है, अतः
ar(ΔAPQ)=12ar(ΔABQ) ...(2)
तथा ΔABC की माध्यिका AQ है, अतः
ar(ΔABQ)=12ar(ΔABC) ...(3)
समीकरण व से (1) व (2) से
ar(ΔPRQ)=12ar(ΔAPQ)
=12×12ar(ΔABQ)
=14ar(ΔABQ)
=14×12ar(ΔABC) [समीकरण (3) से]
∴ar(ΔPRQ)=18ar(ΔABC) ...(4)
∴ΔAPC की माध्यिका CR है, अतः
ar(ΔARC)=12ar(ΔAPC)
=12×12ar(ΔABC)
=14ar(ΔABC) (∵ΔABC की माध्यिका CP है)
⇒ar(ΔABC)=4ar(ΔARC) ...(5)
समीकरण (4) व (5) से,
ar(ΔPRQ)=18×4ar(ΔARC) [समीकरण (5) से]
⇒ar(ΔPRQ)=12ar(ΔARC)
(ii) ar(ΔRQC)=ar(ΔRQA)+ar(ΔAQC)−ar(ΔARC) ....(6)
∵ΔPQA की माध्यिका RQ है, अतः
ar(ΔRQA)=12ar(ΔPQA)=12×12ar(ΔAQB) (ΔAQB की माध्यिका AQ है)
=14ar(ΔAQB)
=14×12ar(ΔABC) (ΔABC की माध्यिका AQ है)
=18ar(ΔABC) ...(7)
∵ΔABC की माध्यिका AQ है, अतः
ar(ΔAQC)=12ar(ΔABC) ...(8)
∵ΔAPC की माध्यिका CR है, अतः
ar(ΔARC)=12ar(ΔAPC)=12×12ar(ΔABC) ....(9) (क्योकि ΔABC की माध्यिका CP है)
अब समीकरण (6), (7), (8) और (9) से
ar(ΔRQC)=18ar(ΔABC)+12ar(ΔABC)−14ar(ΔABC)
=[18+12−14]ar(ΔABC)
=38ar(ΔABC)
(iii) ΔABQ की माध्यिका PQ है, अतः
ar(ΔPBQ)=12ar(ΔABQ)
=12×12ar(ΔABC) (क्योकि ΔABC की माध्यिका AQ है)
=14ar(ΔABC) ...(10)
समीकरण (9) व (10) से,
ar(ΔPBQ)=ar(ΔARC)
Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - अतिलघु उत्तरीय प्रश्न10videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - लघु उत्तरीय प्रश्न10videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.316videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली24videos
चतुर्भुज
Similar Questions
एक समचतुर्भुज के विकर्णों की लम्बाईयाँ 12 सेमी और 16 सेमी है। समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
04:32View Solutionसलंग्न चित्र में, BD = DC और AE = ED है। सिद्ध कीजिए कि ar(ΔACE)=14×ar(ΔABC)
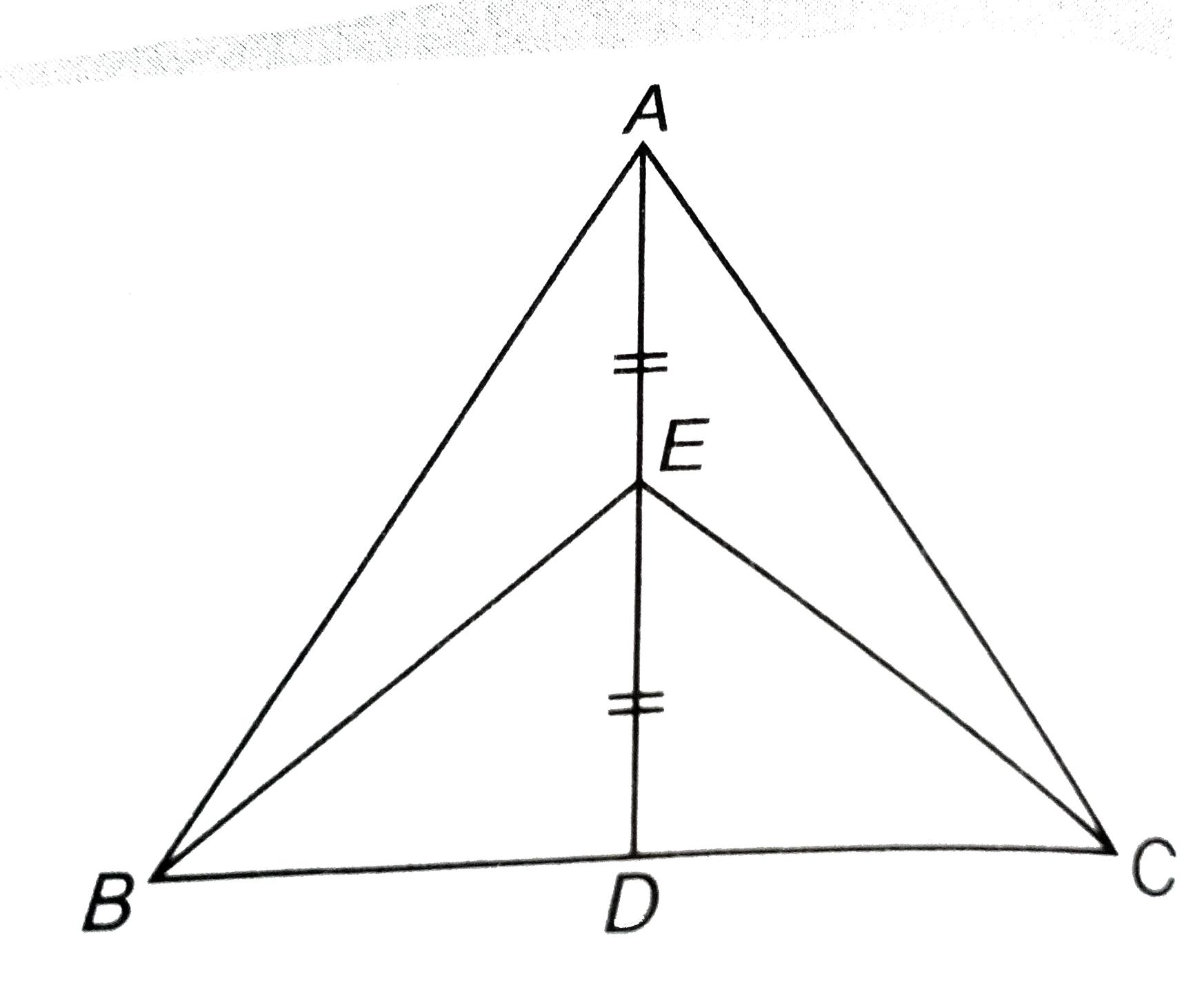 12:05View Solution
12:05View Solutionआकृति में, ΔABC की एक माध्यिका AD पर स्थित E कोई बिन्दु है। दर्शाइए कि ar(ΔABE)=ar(ΔACE) है।
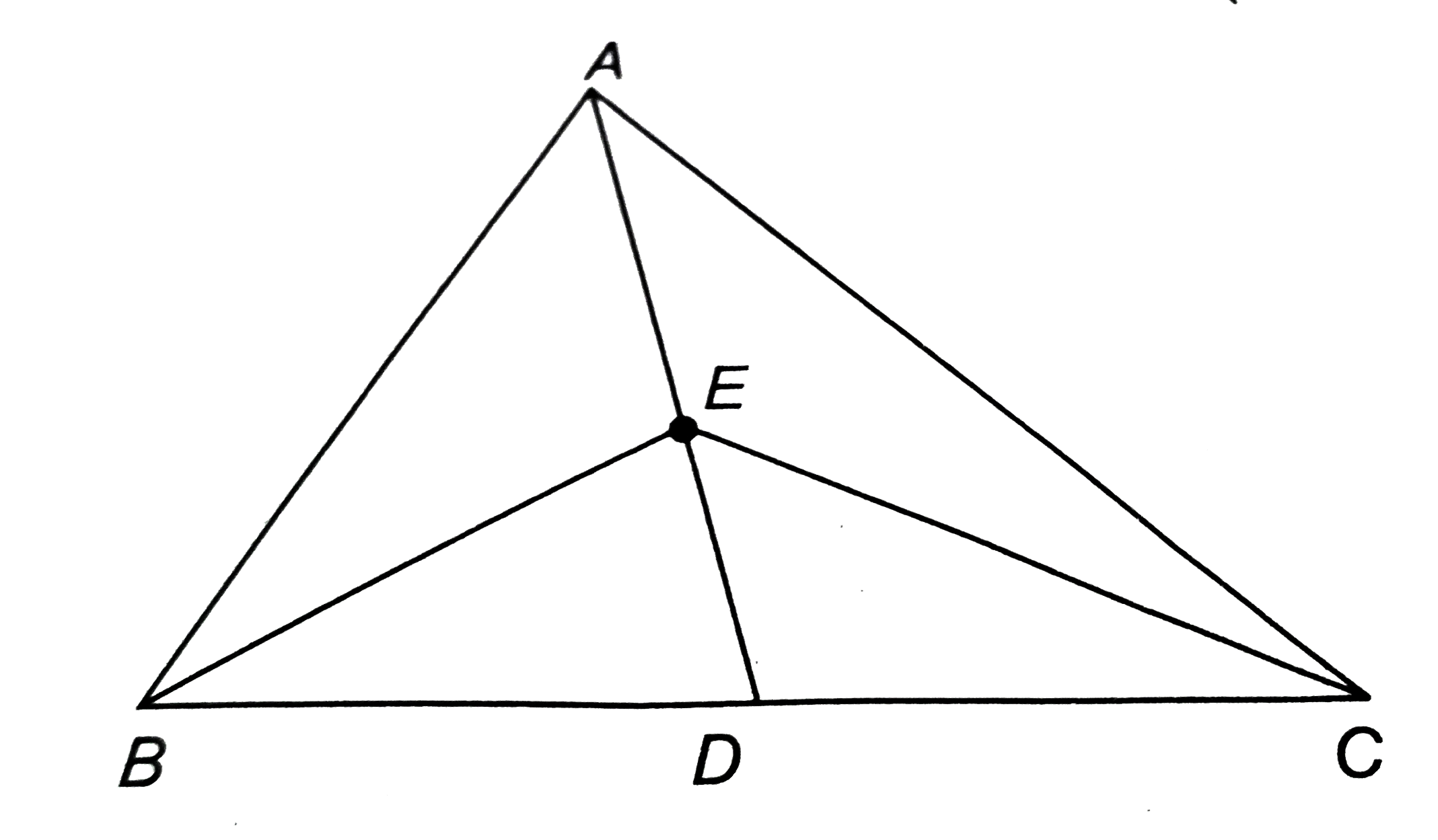 View Solution
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
05:16View SolutionIt is given that ΔABC~ΔPRQandBCQR=23 then ar(ΔPQR)ar(ΔABC)=?
View SolutionΔABC में, भुजाओं AB तथा BC के मध्य-बिंदु क्रमशः P तथा Q है और AP का मध्य-बिंदु R है। सिद्ध कीजिए कि
(i)ar(ΔPBQ)=ar(ΔARC) (ii)ar(ΔPRQ)=12ar(ΔARC)
(iii)ar(ΔRQC)=38ar(ΔABC)View SolutionP और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य बिंदु है तथा R रेखाखण्ड AP का मध्य बिंदु है |दर्शाइए
(i)ar(PQR)=12ar(ARC)
(ii)ar(RQC)=38ar(ABC)05:27View Solutionp और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य बिंदु है तथा R रेखाखण्ड AP का मध्य बिंदु है|दर्शाइए की
ar(PBQ)=ar(ARC)09:36View SolutionIn the following figure , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar (BDE) = 14 ar (ABC)
(ii) ar (BDE) = 12 ar (BAE)
(iii) ar (ABC)= 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 18 ar(AFC)08:15View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid point at AP, show that
(i) ar (PQR) = 12 ar (ARC)
(ii) ar (RQC) = 38 ar (ABC)
(iii) ar (PBQ) = ar (ARC)05:13View SolutionIf the median of a △ABC intersect at G. show that ar (△AGC) = ar (△AGB) = ar (△BGC) = 1/3 ar (△ABC)
04:11View SolutionP and Q are respectively the midpoints of sides AB and BC or a triangle ABC and R is the mid-point of AP, show ar(PRQ)=12 ar(ARC).
01:57View SolutionP and Q are respectively the midpoints of sides AB and BC or a triangle ABC and R is the mid-point of AP, show ar(RQC) = 38 ar(ABC).
03:01View SolutionP and Q are respectively the midpoints of sides AB and BC or a triangle ABC and R is the mid-point of AP, show ar(PBQ)=ar(ARC).
05:07View Solutionਚਿੱਤਰ 9.29 ਵਿਚ,ar (DRC) = ar (DPC) ਹੈ ਅਤੇ ar (BDP) = ar (ARC) ਹੈ।ਦਰਸਾਉ ਕਿ ਦੋਨੋਂ ਚਤੁਰਭੁਜ ABCD ਅਤੇ DCPR ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹਨ।
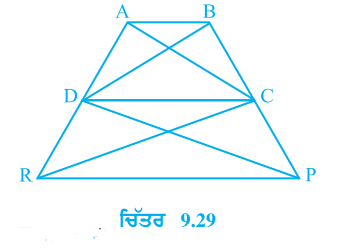 02:50View Solution
02:50View Solution

