आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग है। रेखाखण्ड AX⊥DE भुजा BC को बिन्दु Y पर मिलता है। दर्शाइए कि :
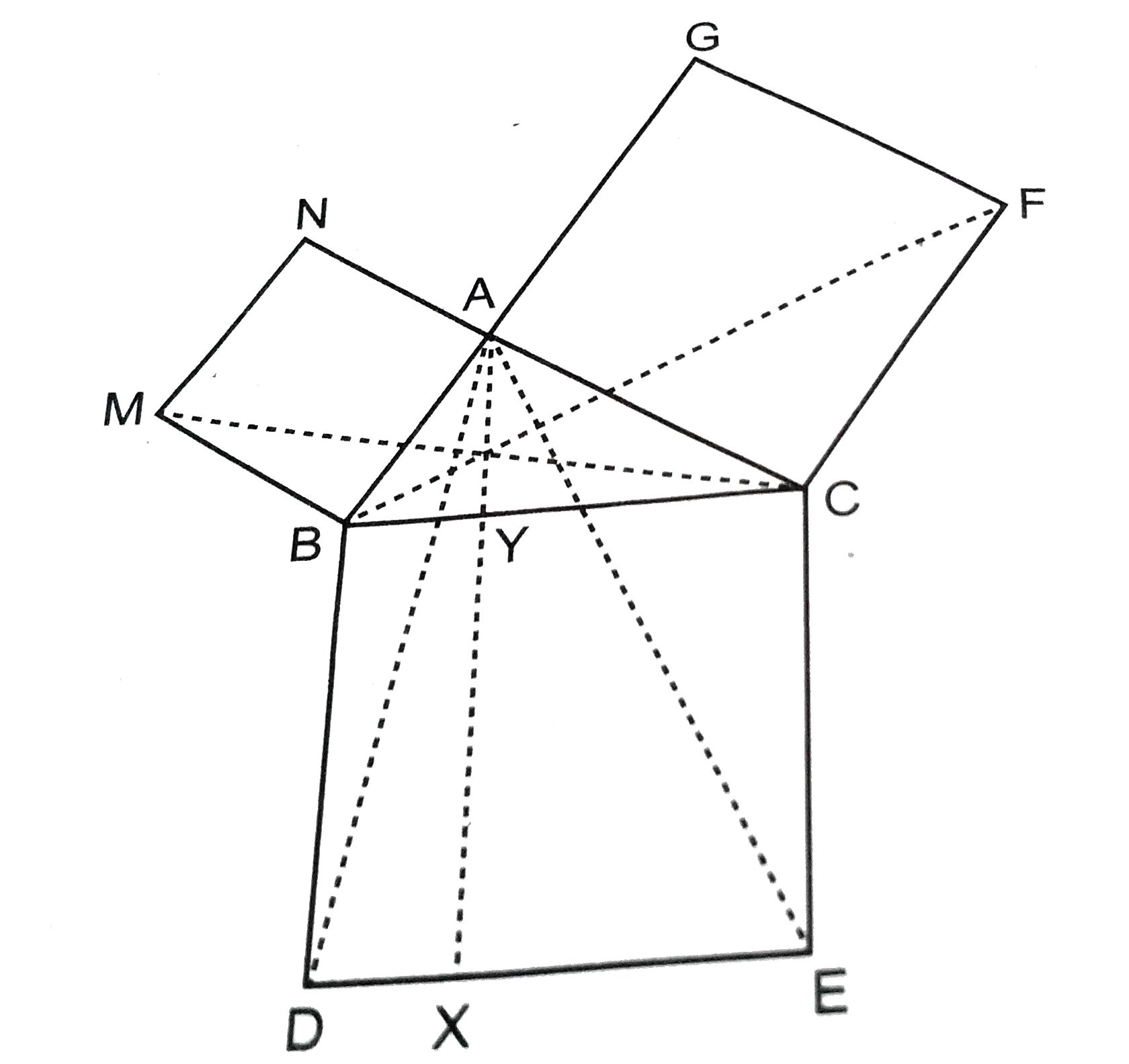
(i) ΔMBC≅ΔABD
(ii) ar(BYXD)=2ar(MBC)
(iii) ar(BYXD) = ar(AMBN)
(iv) ΔFCB≅ΔACE
(v) ar(CYXE)=2ar(FCB)
(vi) ar(CYXE)=ar(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACEG)
टिप्पणी : परिणाम (vii) प्रसिद्ध, (सुपरिचित) पाइथागोरस प्रमेय है। इस प्रमेय की एक सरलतम उपपत्ति आप कक्षा X में पढ़ेंगे।
(i) ΔMBC और ΔABD में,
BC = BD [वर्ग BCED की भुजाएँ]
∠MBC=∠ABD (क्योकि प्रत्येक 90∘+∠ABC)
तथा MB = AB [वर्ग ABMN की भुजाएँ]
अतः ΔMBC≅ΔABD (S.S.S. से)
(ii) अब ΔABD और चतुर्भुज BYXD एक ही आधार BD और एक ही समान्तर रेखाओं BD और AX के बीच स्थित है। अतः
ar(ΔADB)=12ar(BYXD)
परन्तु ΔMBC≅ΔABD [भाग (i) के अनुसार]
⇒ar(ΔMBC)=ar(ΔABD)
∴ar(ΔMBC)=12ar(BYXD) ...(1)
⇒ar(BYXD)=2ar(ΔMBC)
(iii) अब ΔMBC और वर्ग ABMN एक ही आधार MB और एक ही समान्तर रेखाओं MB तथा NC के बीच स्थित है। अतः
ar(ΔMBC)=12ar(ABMN) ...(2)
समीकरण (1) व (2) से
ar(BYXD) = ar(ABMN)
(iv) अब ΔFCB तथा ΔACE में,
CB = CE [वर्ग BCED की भुजाएँ]
∠FCB=∠ACE (क्योकि प्रत्येक कोण 90∘+∠BCA)
तथा FC = AC (वर्ग ACFG की भुजाएँ)
अतः ΔFCB≅ΔACE (S.A.S. से)
(v) ΔACE और चतुर्भुज CYXE एक ही आधार CE और एक ही समान्तर रेखाओं CE तथा AX के बीच स्थित है अतः
ar(ACE)=12ar(CYXE)
⇒12ar(CYXE)=ar(ΔFCB) [भाग (iii) से]
⇒ar(CYXE)=2ar(ΔFCB)
(vi) वर्ग ACFG और ΔBCF एक ही आधार CF और BG एक ही समान्तर रेखाओं और के बीच स्थित है अतः
ar(ΔBCF)=12ar(ACFG)
तथा ar(ΔFCB)=12ar(CYXE)
अतः 12ar(CYXE)=12ar(ACFG)
⇒ar(CYXE)=ar(ACFG)
(vii) ΔACB के पाइथागोरस प्रमेय से
BC2=AB2+AC2
⇒BC×BD=AB×MB+AC+FC
⇒ar(BCED)=ar(ABMN)+ar(ADFG)
Topper's Solved these Questions
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - अतिलघु उत्तरीय प्रश्न
10 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - लघु उत्तरीय प्रश्न
10 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.3
16 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
Similar Questions
एक समचतुर्भुज के विकर्णों की लम्बाईयाँ 12 सेमी और 16 सेमी है। समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionसलंग्न चित्र में, BD = DC और AE = ED है। सिद्ध कीजिए कि ar(ΔACE)=14×ar(ΔABC)
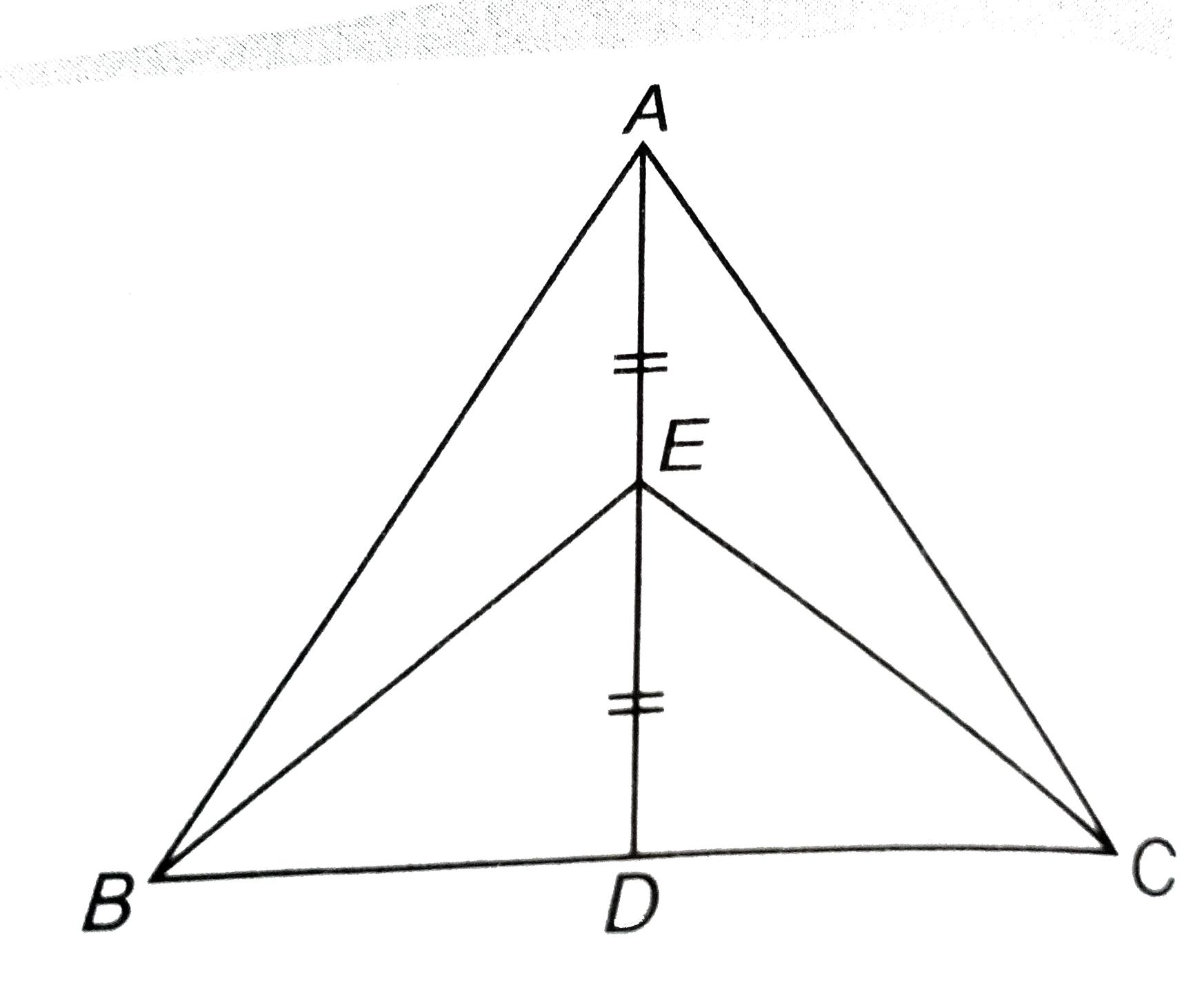
View Solutionआकृति में, ΔABC की एक माध्यिका AD पर स्थित E कोई बिन्दु है। दर्शाइए कि ar(ΔABE)=ar(ΔACE) है।
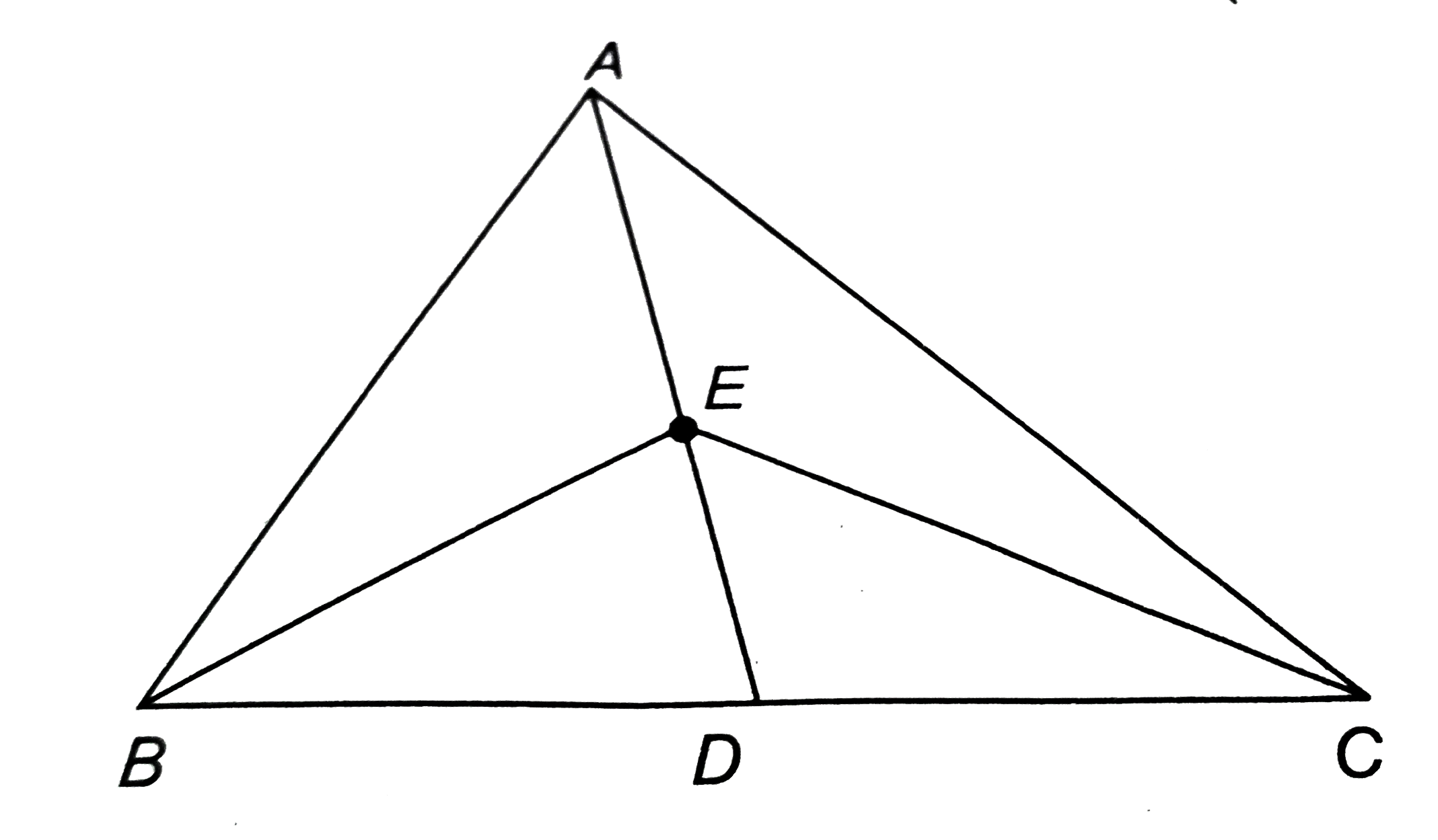
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionदी गए आकृति में ABC एक समकोण त्रिभुज है जिसके कोण A समकोण है | BCED,ACFG और ABMN क्रमशः भुजाओं BC ,CA और AB पर बने वर्ग है| रेखाखण्ड AX⊥DE भुजा BC से बिंदु Y पर मिलता हैं |दर्शाइए की :
(i)ΔMBC≡ΔABD
(ii)ar(BYXD)=2ar(MBC)
(iii)ar(BYXD)=ar(ABMN)
(iv) ΔFCB=ΔACE
(v)ar(CYXE)=2ar(FCB)
(vi)ar(CYXE)=ar(ACFG)
(vii)ar(BCED)=ar(ABMN)+ar(ACFG)
(viii)BC2=AB2+AC2
(##KCSHINMATIXC11SLV032_Q01##)
View SolutionF,Cl, Br ,I and Ar are collectively known as ____________.
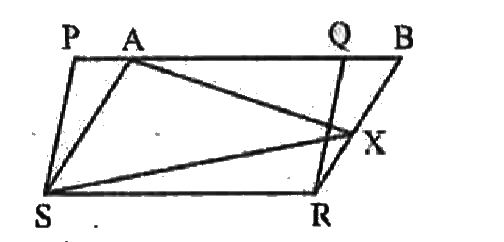
View SolutionIn, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
ar (PQRS) = ar (ABRS)
as (AXS) = 12 ar (PQRS)
View SolutionFactorise:
ar+br+at+bt
View SolutionIn the following figure , ABC is a right triangle right angled at A. BCED ACFG and ABMN and squares on the sides BC, CA and AB respectively , Line segement AX ⊥ DE meets BC at Y. Show that
(i) ti⟩MBC=ti⟩(MBC)
(ii) ar (BXYD) = 2 ar (MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ti⟩FCB=ti⟩ACE
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE ) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
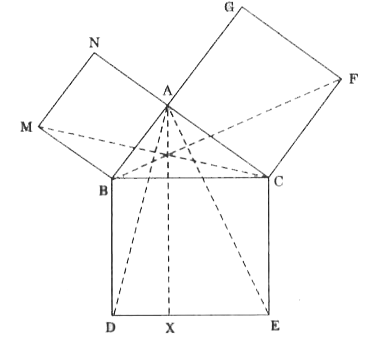
View Solutionआकृति में PQRS और ABRS समांतर चतुर्भज है तथा x भुजा BR पर स्थित कोई बिंदु है। दर्शाइए कि
ar(AXS)=12ar(PQRS)
View SolutionPQRS and ABRS are parallelograms and X is any point on the side BR. Show that
(i) ar(PQRS) = ar(ABRS)
(ii) ar(ΔAXS)=12ar(PQRS)
View SolutionIn the Fig Prove that XA+AR=XB+BR.
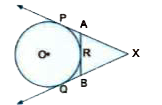
View Solutionगुणनखण्ड निकालें:
ar+br+at+bt
View Solutionਚਿੱਤਰ 9.17 ਵਿੱਚ,PQRS ਅਤੇ ABRS ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹਨ ਅਤੇ X ਭੁਜਾ BR ਉੱਤੇ ਸਥਿਤ ਕੋਈ ਬਿੰਦੂ ਹੈ। ਦਰਸਾਉ ਕਿ (i) ar (PQRS) = ar (ABRS) (ii) ar (AX S) =12ar(PQRS)
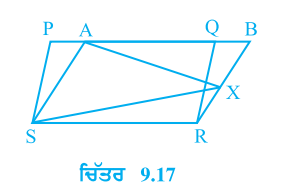
View Solutionar + br + at + bt = __
View SolutionIn shape, ABC There is a right angled triangle whose angle A is right angled. BCED,ACFG And ABMN sides respectively BC, CA And AB There are classes built on. Line segment AX_|_DE arm BC meets at point Y. Show that: ar (BYXD) =2 ar (MBC)
View Solution
