Complete Solutions to EXERCISE of chapter ਤ੍ਰਿਭੁਜਾਂ of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | ਤ੍ਰਿਭੁਜਾਂ |
| PSEB (PUNJABI MEDIUM) | EXERCISE |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
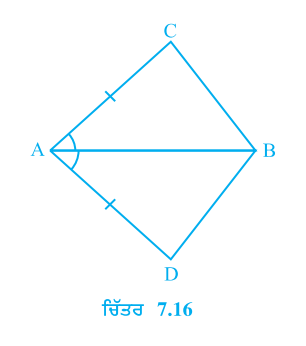
ਚਤੁਰਭੁਜ ABCD ਵਿਚ, AC = AD ਅਤੇ AB `angle A` ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੀ ਹੈ(ਦੇਖੋ ਚਿੱਤਰ 7.16)। ਸਿੱਧ ਕਰੋ ਕਿ `triangle ABC cong triangle ABD` ਤੁਸੀਂ BC ਅਤੇ BD ਬਾਰੇ ਕੀ ਕਹਿੰਦੇ ਹੋ?
 04:06View Solution
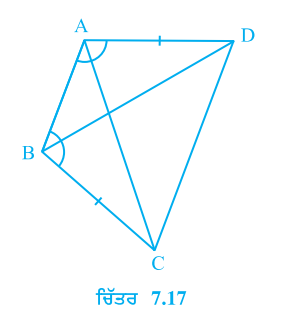
04:06View SolutionABCD ਇਕ ਚਤੁਰਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ AD = BC ਅਤੇ `angle DAB =angle CBA` ਹੈ(ਵੇਖੋ ਚਿੱਤਰ 7.17)। ਸਿੱਧ ਕਰੋ (i) `triangle ABD cong triangle BAC` (ii) BD = AC (iii) `angle ABD = angle BAC`
 04:37View Solution
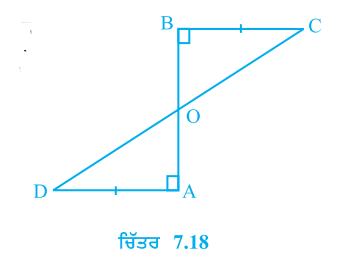
04:37View Solutionਰੇਖਾਖੰਡ AB 'ਤੇ AD ਅਤੇ BC ਲੰਬ ਹਨ(ਵੇਖੋ ਚਿੱਤਰ 7.18)। ਸਿੱਧ ਕਰੋ ਕਿ CD ਰੇਖਾ ਖੰਡ AB ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੀ ਹੈ।
 04:12View Solution
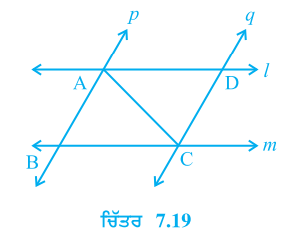
04:12View Solutionਦੋ ਸਮਾਨੰਤਰ ਰੇਖਾਵਾਂ l ਅਤੇ m, ਇਕ ਹੋਰ ਸਮਾਨੰਤਰ ਰੇਖਾਵਾਂ ਦੇ ਜੋੜੇ p ਅਤੇ q ਦੁਵਾਰਾ ਕੱਟੀਆਂ ਜਾਂਦੀਆਂ ਹਨ(ਵੇਖੋ ਚਿੱਤਰ 7.19)।ਸਿੱਧ ਕਰੋ ਕਿ `triangle ABC cong triangle CDA` ਹੈ।
 02:48View Solution
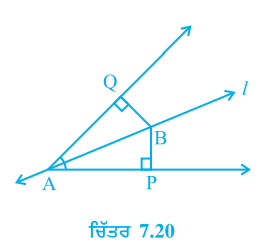
02:48View Solutionਰੇਖਾ l, `angle A` ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੀ ਹੈ ਅਤੇ B, l ਉੱਤੇ ਕੋਈ ਬਿੰਦੂ ਹੈ।BP ਅਤੇ BQ ਬਿੰਦੂ B ਤੋਂ `angle A` ਦੀਆਂ ਬਾਹਵਾਂ ਉੱਤੇ ਲੰਬ ਹਨ (ਵੇਖੋ ਚਿੱਤਰ 7.20)। ਸਿੱਧ ਕਰੋ (i) `triangle APB cong triangle AQB` (ii) BP = BQ ਜਾਂ B ਬਿੰਦੂ ਕੋਣ A ਦੀਆਂ ਭੁਜਾਵਾਂ ਤੋਂ ਸਮਾਨ ਦੂਰੀ 'ਤੇ ਹੈ।
 05:36View Solution
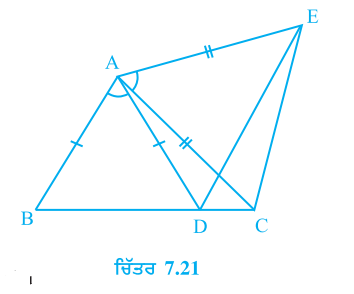
05:36View Solutionਚਿੱਤਰ 7.21 ਵਿਚ AC = AE, AB = AD, ਅਤੇ `angle BAD = angle EAC` ਹੈ। ਸਿੱਧ ਕਰੋ BC =DE
 03:41View Solution
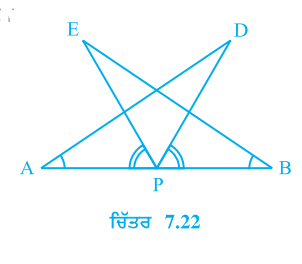
03:41View SolutionAB ਇੱਕ ਰੇਖਾ ਖੰਡ ਹੈ ਅਤੇ P ਇਸਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ। D ਅਤੇ E ਰੇਖਾਖੰਡ AB ਦੇ ਇਕੋ ਪਾਸੇ ਦੋ ਬਿੰਦੂ ਇਸ ਤਰ੍ਹਾਂ ਹਨ ਕਿ `angle BAD = angle ABE` ਅਤੇ `angle EPA = angle DPB` (ਵੇਖੋ ਚਿੱਤਰ 7.22 ) ਸਿੱਧ ਕਰੋ(i) `triangle DAP cong triangle EBP` (ii) AD = BE
 04:42View Solution
04:42View Solutionਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਵਿੱਚ AB = AC,`angle B` ਅਤੇ `angle C ` ਦੇ ਸਮਦੁਭਾਜਕ ਇੱਕ ਦੂਸਰੇ ਨੂੰ O 'ਤੇ ਕੱਟਦੇ ਹਨ। A ਅਤੇ O ਨਾਲ ਮਿਲਾਉ। ਸਿੱਧ ਕਰੋ:-(i) OB = OC (ii) AO , `angle A` ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦਾ ਹੈ।
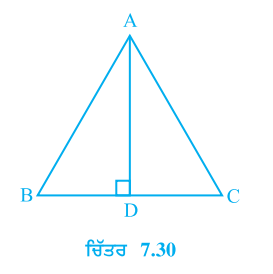
09:25View Solution`triangle ABC` ਵਿੱਚ AD ਭੁਜਾ BC ਦਾ ਲੰਬ ਸਮਦੁਭਾਜਕ ਹੈ ਦੇਖੋ ਚਿੱਤਰ 7.30)। ਸਿੱਧ ਕਰੋ ਕਿ `triangle ABC` ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ AB = AC ਹੈ।
 04:21View Solution
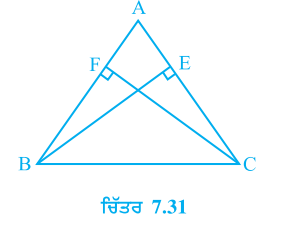
04:21View SolutionABC ਇੱਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ BE ਅਤੇ CF ਸਮਾਨ ਭੁਜਾਵਾਂ AC ਅਤੇ AB 'ਤੇ ਖਿੱਚੇ ਗਏ ਸਿਖਰ ਲੰਬ ਹਨ (ਦੇਖੋ ਚਿੱਤਰ 7.31)। ਸਿੱਧ ਕਰੋ ਕਿ ਇਹ ਸਿਖਰ ਲੰਬ ਸਮਾਨ ਹੈ।
 03:11View Solution
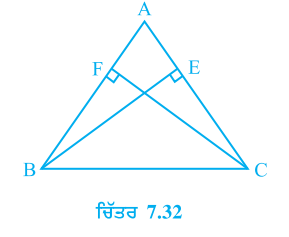
03:11View SolutionABC ਇੱਕ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ ਭੁਜਾਵਾਂ AC ਅਤੇ AB ਉੱਤੇ ਸਿਖਰਲੰਬ BE ਅਤੇ CF ਬਰਾਬਰ ਹਨ (ਦੇਖੋ ਚਿੱਤਰ 7.32)। ਸਿੱਧ ਕਰੋ ਕਿ (i) `triangle ABE cong triangle ACF` (ii) AB = AC ਜਾਂ `triangle ABC` ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ।
 04:05View Solution
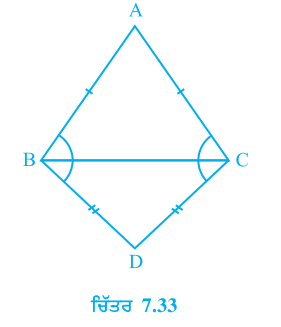
04:05View SolutionABC ਅਤੇ DBC ਇਕੋ ਆਧਾਰ BC ਉੱਤੇ ਦੋ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜਾਂ ਹਨ (ਵੇਖੋ ਚਿੱਤਰ 7.33)। ਸਿੱਧ ਕਰੋ `angle ABD = angle ACD`
 02:25View Solution
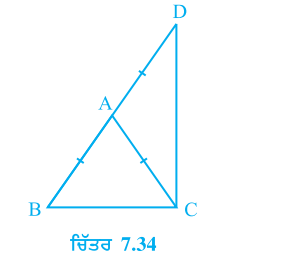
02:25View SolutionABC ਇੱਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ। ਜਿਸ ਵਿਚ AB=AC ਹੈ। ਭੁਜਾ BA ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਵਧਾਇਆ ਗਿਆ ਹੈ ਕਿ ਉਹ D 'ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਮਿਲਦੀ ਹੈ ਕਿ AD=AB (ਵੇਖੋ ਚਿੱਤਰ 7.34) ਹੋਵੇ।ਸਿੱਧ ਕਰੋ `angle BCD` ਇਕ ਸਮਕੋਣ ਹੈ।
 04:57View Solution
04:57View SolutionABC ਇੱਕ ਸਮਕੋਣੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ `angle A = 90^@` ਅਤੇ AB=AC ਹੈ। `angle B` ਅਤੇ `angle C` ਪਤਾ ਕਰੋ।
03:19View Solutionਸਿੱਧ ਕਰੋ ਕਿ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਦਾ ਹਰੇਕ ਕੋਣ `60^@` ਹੁੰਦਾ ਹੈ।
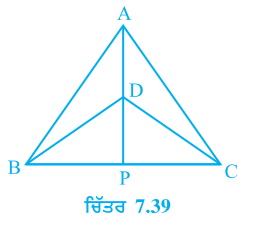
02:41View Solution`triangle ABC` ਅਤੇ `triangle DBC` ਇੱਕ ਹੀ ਆਧਾਰ BC ਉਤੇ ਦੋ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜਾਂ ਹਨ ਅਤੇ ਸਿਖਰ A ਅਤੇ D ਭੁਜਾ BC ਦੇ ਇਕੋ ਪਾਸੇ ਹਨ (ਵੇਖੋ ਚਿੱਤਰ 7.39)। ਜੇ ਭੁਜਾ AD ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਵਧਾਇਆ ਜਾਵੇ ਕਿ ਭੁਜਾ BC ਨੂੰ P 'ਤੇ ਕੱਟੇ ਤਾਂ ਸਿੱਧ ਕਰੋ ਕਿ `triangle ABD cong triangle ACD`
 06:30View Solution
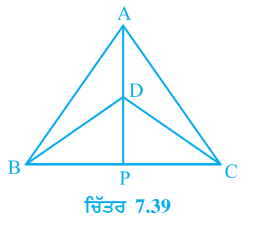
06:30View Solution`triangle ABC` ਅਤੇ `triangle DBC` ਇੱਕ ਹੀ ਆਧਾਰ BC ਉਤੇ ਦੋ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜਾਂ ਹਨ ਅਤੇ ਸਿਖਰ A ਅਤੇ D ਭੁਜਾ BC ਦੇ ਇਕੋ ਪਾਸੇ ਹਨ (ਵੇਖੋ ਚਿੱਤਰ 7.39)। ਜੇ ਭੁਜਾ AD ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਵਧਾਇਆ ਜਾਵੇ ਕਿ ਭੁਜਾ BC ਨੂੰ P 'ਤੇ ਕੱਟੇ ਤਾਂ ਸਿੱਧ ਕਰੋ ਕਿ`triangle ABP cong triangle ACP`
 03:42View Solution
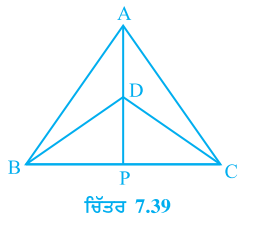
03:42View Solution`triangle ABC` ਅਤੇ `triangle DBC` ਇੱਕ ਹੀ ਆਧਾਰ BC ਉਤੇ ਦੋ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜਾਂ ਹਨ ਅਤੇ ਸਿਖਰ A ਅਤੇ D ਭੁਜਾ BC ਦੇ ਇਕੋ ਪਾਸੇ ਹਨ (ਵੇਖੋ ਚਿੱਤਰ 7.39)। ਜੇ ਭੁਜਾ AD ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਵਧਾਇਆ ਜਾਵੇ ਕਿ ਭੁਜਾ BC ਨੂੰ P 'ਤੇ ਕੱਟੇ ਤਾਂ ਸਿੱਧ ਕਰੋ ਕਿ AP, `angle A` ਅਤੇ `angle D` ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੀ ਹੈ।
 06:15View Solution
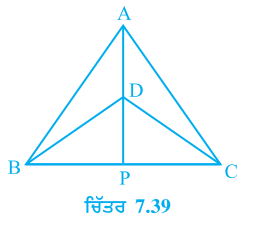
06:15View Solution`triangle ABC` ਅਤੇ `triangle DBC` ਇੱਕ ਹੀ ਆਧਾਰ BC ਉਤੇ ਦੋ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜਾਂ ਹਨ ਅਤੇ ਸਿਖਰ A ਅਤੇ D ਭੁਜਾ BC ਦੇ ਇਕੋ ਪਾਸੇ ਹਨ (ਵੇਖੋ ਚਿੱਤਰ 7.39)। ਜੇ ਭੁਜਾ AD ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਵਧਾਇਆ ਜਾਵੇ ਕਿ ਭੁਜਾ BC ਨੂੰ P 'ਤੇ ਕੱਟੇ ਤਾਂ ਸਿੱਧ ਕਰੋ ਕਿ AP, ਭੁਜਾ BC ਦਾ ਲੰਬ ਸਮਦੁਭਾਜਕ ਹੈ।
 04:34View Solution
04:34View SolutionAD ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਦਾ ਸਿਖਰਲੰਬ ਹੈ, ਜਿਸ ਵਿੱਚ AB=AC ਹੈ ਸਿੱਧ ਕਰੋ AD, BC ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੀ ਹੈ।
06:21View SolutionAD ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਦਾ ਸਿਖਰਲੰਬ ਹੈ, ਜਿਸ ਵਿੱਚ AB=AC ਹੈ ਸਿੱਧ ਕਰੋ AD,ਕੋਣ A ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੀ ਹੈ।
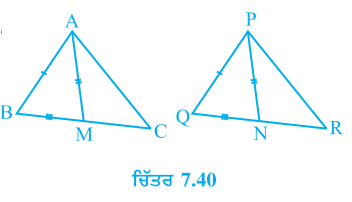
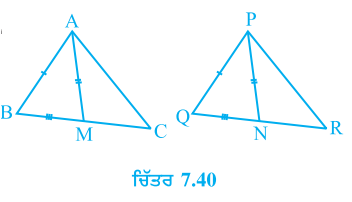
05:00View Solutionਤ੍ਰਿਭੁਜ ABC ਦੀਆਂ ਦੋ ਭੁਜਾਵਾਂ AB,BC ਅਤੇ ਮੱਧਿਕਾ AM ਕ੍ਰਮਵਾਰ ਦੂਸਰੀ ਤ੍ਰਿਭੁਜ PQR ਦੀਆਂ ਭੁਜਾਵਾਂ PQ ਅਤੇ QR ਅਤੇ ਮੱਧਿਕਾ PN ਦੇ ਬਰਾਬਰ ਹਨ (ਵੇਖੋ ਚਿੱਤਰ 7.40)। ਸਿੱਧ ਕਰੋ ਕਿ `triangle ABM cong triangle PQN`
 06:01View Solution
06:01View Solutionਤ੍ਰਿਭੁਜ ABC ਦੀਆਂ ਦੋ ਭੁਜਾਵਾਂ AB,BC ਅਤੇ ਮੱਧਿਕਾ AM ਕ੍ਰਮਵਾਰ ਦੂਸਰੀ ਤ੍ਰਿਭੁਜ PQR ਦੀਆਂ ਭੁਜਾਵਾਂ PQ ਅਤੇ QR ਅਤੇ ਮੱਧਿਕਾ PN ਦੇ ਬਰਾਬਰ ਹਨ (ਵੇਖੋ ਚਿੱਤਰ 7.40)। ਸਿੱਧ ਕਰੋ ਕਿ `triangle ABC cong triangle PQR`
 03:47View Solution
03:47View SolutionBE ਅਤੇ CF ਤ੍ਰਿਭੁਜ ABC ਦੇ ਦੋ ਸਮਾਨ ਸਿਖਰ ਲੰਬ ਹਨ। ਸ-ਕ-ਭੁ(RHS) ਸਰਬੰਗਸਮਤਾ ਨਿਯਮ ਵਰਤਦੇ ਹੋਏ ਸਿੱਧ ਕਰੋ ਕਿ ਤ੍ਰਿਭੁਜ ABC ਸਮਦੋਭੁਜੀ ਹੈ।
03:48View SolutionABC ਇੱਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ AB=AC ਹੈ। `AP bot BC` ਖਿੱਚ ਕੇ ਦਰਸਾਓ ਕਿ `angle B = angle C` ਹੈ।
03:00View Solutionਦਿਖਾਓ ਕਿ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਵਿੱਚ ਕਰਣ ਸਭ ਤੋਂ ਲੰਬੀ ਭੁਜਾ ਹੁੰਦੀ ਹੈ।
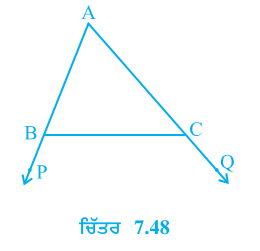
04:38View Solutionਚਿੱਤਰ 7.48 ਵਿੱਚ, `triangle ABC` ਦੀਆਂ ਭੁਜਾਵਾਂ AB ਅਤੇ AC ਨੂੰ ਕ੍ਰਮਵਾਰ ਬਿੰਦੂਆਂ P ਅਤੇ Q ਤੱਕ ਵਧਾਇਆ ਗਿਆ ਹੈ। ਨਾਲ ਹੀ, `angle PBC < angle QCB` ਹੈ। ਦਿਖਾਓ ਕਿ AC > AB ਹੈ।
 04:04View Solution
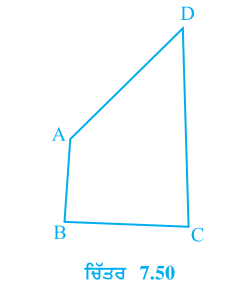
04:04View SolutionAB ਅਤੇ CD ਕ੍ਰਮਵਾਰ ਇੱਕ ਚਤੁਰਭੁਜ ABCD ਦੀ ਸਭ ਤੋਂ ਛੋਟੀ ਅਤੇ ਸਭ ਤੋਂ ਵੱਡੀ ਭੁਜਾ ਹੈ (ਦੇਖੋ ਚਿੱਤਰ 7.50)। ਦਿਖਾਓ ਕਿ `angle A > angle C` ਅਤੇ `angle B > angle D` ਹੈ।
 04:25View Solution
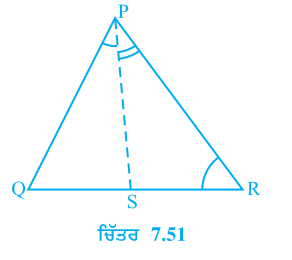
04:25View Solutionਚਿੱਤਰ 7.51 ਵਿੱਚ,PR > PQ ਹੈ ਅਤੇ PS, ਕੋਣ QPR ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦਾ ਹੈ। ਸਿੱਧ ਕਰੋ ਕਿ `angle PSR > angle PSQ` ਹੈ।
 04:06View Solution
04:06View Solutionਦਿਖਾਓ ਕਿ ਇੱਕ ਰੇਖਾ ਉੱਤੇ ਇੱਕ ਦਿੱਤੇ ਹੋਏ ਬਿੰਦੂ ਨਾਲ, ਜੋ ਉਸ ਰੇਖਾ ਉਪਰ ਸਥਿਤ ਨਹੀਂ ਹੈ, ਜਿੰਨੇ ਵੀ ਰੇਖਾ ਖੰਡ ਖਿੱਚੇ ਜਾ ਸਕਦੇ ਹਨ ਉਹਨਾਂ ਵਿੱਚੋਂ ਲੰਬ ਰੇਖਾਖੰਡ ਸਭ ਤੋਂ ਛੋਟਾ ਹੁੰਦਾ ਹੈ।
04:23View Solution
EXERCISE questions and complete solutions for chapter ਤ੍ਰਿਭੁਜਾਂ of PSEB (PUNJABI MEDIUM) of Class 9
