Complete Solutions to EXERCISE of chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREAS OF PARALLELOGRAMS AND TRIANGLES |
| PSEB | EXERCISE |
| Number Of Questions | 52 |
| Academic Year | 2023-24 |
Which of the following figures

 lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
View SolutionWhich of the following figures

 lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
View SolutionWhich of the following figures

 lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
View SolutionWhich of the following figures

 lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
View SolutionWhich of the following figures

 lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
View SolutionWhich of the following figures

 lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
View SolutionABCD is a parallelogram, `AE bot DC` and `CF bot AD`. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
View SolutionIf E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH)`=1/2`ar(ABCD).
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
View SolutionIn Fig.
 , P is a point in the interior of a parallelogram ABCD. Show that `ar(APB)+ar(PCD)=1/2ar(ABCD)`.
, P is a point in the interior of a parallelogram ABCD. Show that `ar(APB)+ar(PCD)=1/2ar(ABCD)`.
View SolutionIn fig.
 PQRS and ABRS are parallelograms and X is any point on side BR. Show that `ar(PQRS)=ar(ABRS)`.
PQRS and ABRS are parallelograms and X is any point on side BR. Show that `ar(PQRS)=ar(ABRS)`.
View SolutionA farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q.In how many parts the field is divided ? What are the shapes of these parts ? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it ?
View SolutionE is any point on median AD of a `triangle ABC` . Show that ar (ABE) = ar (ACE).
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE)=`1/4` ar(ABC).
View SolutionA diagonal of parallelogram divides it into four triangles of equal area.
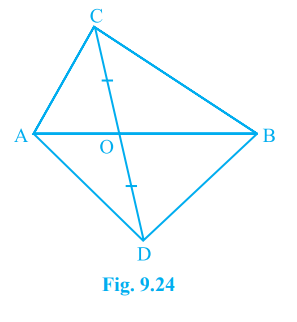
View SolutionIn Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar(ABC) = ar (ABD).
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a `triangle ABC`. Show that:- BDEF is a parallelogram.
View SolutionD, E and F are respectively the mid¬ points of the sides BC, CA and AB of `triangleABC`. Determine the ratio of the areas of triangles DEF and ABC.
View SolutionD, E and F are respectively the mid¬ points of the sides BC, CA and AB of `triangleABC`. Determine the ratio of the areas of triangles DEF and ABC.
View SolutionIn Fig.
 diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that : ar (DOC)=ar (AOB).
diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that : ar (DOC)=ar (AOB).
View SolutionIn Fig.
 diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that : ar (DCB)=ar (ACB).
diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that : ar (DCB)=ar (ACB).
View SolutionIn Fig.
 diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that : `DA||CB` or ABCD is a parallelogram.
diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that : `DA||CB` or ABCD is a parallelogram.
View SolutionD and E are points on sides AB and AC respectively of `DeltaABC` such that ar (DBC) = ar (EBC). Prove that `DE II BC`.
View SolutionXY is a line parallel to side BC of triangle ABC. If `BE II AC` and `CF II AB` meet XY at E and F respectively,show that ar (ABE) = ar (ACF).
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed . Show that ar (ABCD) = ar (PBQR). [Hint : Join AC and PQ. Now compare ar (ACQ) and ar (APQ).]

View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
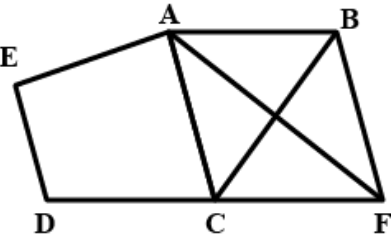
View SolutionIn Fig. 9.27, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that:- (i) ar (ACB) = ar (ACF) (ii) ar (AEDF) = ar (ABCDE)
View SolutionABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY). [Hint : Join CX.]
View SolutionIn Fig
 , `AP II BQ II CR`. Prove that ar (AQC) = ar (PBR).
, `AP II BQ II CR`. Prove that ar (AQC) = ar (PBR).
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
View SolutionIn Fig.
 , ar (ABQ) = ar (PBQ) and ar (BQC) = ar (BQR). Show that both the quadrilaterals ABQP and BCRQ are trapeziums.
, ar (ABQ) = ar (PBQ) and ar (BQC) = ar (BQR). Show that both the quadrilaterals ABQP and BCRQ are trapeziums.
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionIn fig.
 , D and E are two points on BC such that `BD = DE = EC`. Show that ar (ABD) = ar (ADE) = ar (AEC). Can you now answer the question that you have left in the ‘introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area ?
, D and E are two points on BC such that `BD = DE = EC`. Show that ar (ABD) = ar (ADE) = ar (AEC). Can you now answer the question that you have left in the ‘introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area ?
View SolutionIn Fig.
 ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).
ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).
View SolutionIn Fig.
 ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
View SolutionIn Fig.
 , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar (BDE)=`1/4`ar(ABC).
, ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar (BDE)=`1/4`ar(ABC).
View SolutionIn Fig.
 , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar (BDE)=`1/2`ar(BAE).
, ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar (BDE)=`1/2`ar(BAE).
View SolutionIn Fig.
 , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar(ABC)=2 ar(BEC).
, ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar(ABC)=2 ar(BEC).
View SolutionIn Fig.
 , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar(BFE)=ar(AFD).
, ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar(BFE)=ar(AFD).
View SolutionIn Fig.
 , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar(BFE)=2ar(FED).
, ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar(BFE)=2ar(FED).
View SolutionIn Fig.
 , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar(FED)=`1/8` ar(AFC).
, ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that : ar(FED)=`1/8` ar(AFC).
View SolutionDiagonals AC and BD of quadrilateral ABCD intersect each other at P. Show that ar `(APB) xx ar (CPD)` = ar `(APD)xx ar(BPC)`.
View SolutionP and Q are respectively the midpoints of sides AB and BC or a triangle ABC and R is the mid-point of AP, show ar(PRQ)=`1/2` ar(ARC).
View SolutionP and Q are respectively the midpoints of sides AB and BC or a triangle ABC and R is the mid-point of AP, show ar(RQC) = `3/8` ar(ABC).
View SolutionP and Q are respectively the midpoints of sides AB and BC or a triangle ABC and R is the mid-point of AP, show ar(PBQ)=ar(ARC).
View SolutionIn Fig.
 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment `AX _|_ DE` meets BC at Y. Show that : `DeltaMBC ~= DeltaABD`.
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment `AX _|_ DE` meets BC at Y. Show that : `DeltaMBC ~= DeltaABD`.
View SolutionIn Fig.
 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment `AX _|_ DE` meets BC at Y. Show that : ar (BYXD)=2ar(MBC).
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment `AX _|_ DE` meets BC at Y. Show that : ar (BYXD)=2ar(MBC).
View SolutionIn Fig.
 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment `AX _|_ DE` meets BC at Y. Show that : ar(BYXD)=ar(ABMN).
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment `AX _|_ DE` meets BC at Y. Show that : ar(BYXD)=ar(ABMN).
View SolutionIn Fig.
 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment `AX _|_ DE` meets BC at Y. Show that : `DeltaFCB ~= DeltaACE`.
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment `AX _|_ DE` meets BC at Y. Show that : `DeltaFCB ~= DeltaACE`.
View SolutionIn Fig.
 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment `AX _|_ DE` meets BC at Y. Show that : ar(CYXE)=2ar(FCB).
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment `AX _|_ DE` meets BC at Y. Show that : ar(CYXE)=2ar(FCB).
View SolutionIn Fig.
 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment `AX _|_ DE` meets BC at Y. Show that : ar(CYXE)=ar(ACFG).
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment `AX _|_ DE` meets BC at Y. Show that : ar(CYXE)=ar(ACFG).
View SolutionIn Fig.
 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment `AX _|_ DE` meets BC at Y. Show that : ar(BCED)=ar(ABMN)+ar(ACFG).
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment `AX _|_ DE` meets BC at Y. Show that : ar(BCED)=ar(ABMN)+ar(ACFG).
View Solution
EXERCISE questions and complete solutions for chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of PSEB of Class 9