Complete Solutions to EXERCISE 1.6 of chapter SET LANGUAGE of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | SET LANGUAGE |
| SURA PUBLICATION | EXERCISE 1.6 |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
If n(A) = 25, n(B) = 40, `n(AcupB)=50` and n(B') = 25, find `n(AcapB)` and n(U).
View SolutionIf n(A) = 300, `n(AcupB)=500,n(AcapB)=50` and n(B') = 350, find n(B) and n(U).
View SolutionIf `U={x:x inNN,xle10}`, A = {2, 3, 4, 8, 10} and B = {1, 2, 5, 8, 10}, then verify that `n(AcupB)=n(A)+n(B)-n(AcapB)`
View SolutionVerify `n(AcupBcupC)=n(A)+n(B)+n(C)-n(AcapB)-n(BcapC)-n(AcapC)+n(AcapBcapC)` for the following sets.
(i) A{a, c, e, f, h}, B = {c, d, e, f} and C = {a, b, c, f}
(ii) A = {1, 3, 5} B = {2, 3, 5, 6} and C = {1, 5, 6, 7}.
View SolutionIn a class, all students take part in either music or drama or both. 25 students take part in music, 30 students take part in drama and 8 students take part in both music and drama. Find
(i) The number of students who take part in only music.
(ii) The number of students who take part in only drama.
(iii) The total number of students in the class.
View SolutionIn a party of 45 people, each one likes tea or coffee or both. 35 people like tea and 20 people like coffee. Find the number of people who
(i) like both tea and coffee.
(ii) do not like tea.
(iii) do not like coffee.
View SolutionIn an examination 50% of the students passed in Mathematics and 70% of students passed in Science while 10% students failed in both subjects. 300 students passed in atleast one subjects. Find the total number of students who appeared in the examination, if they took examination in only two subjects.
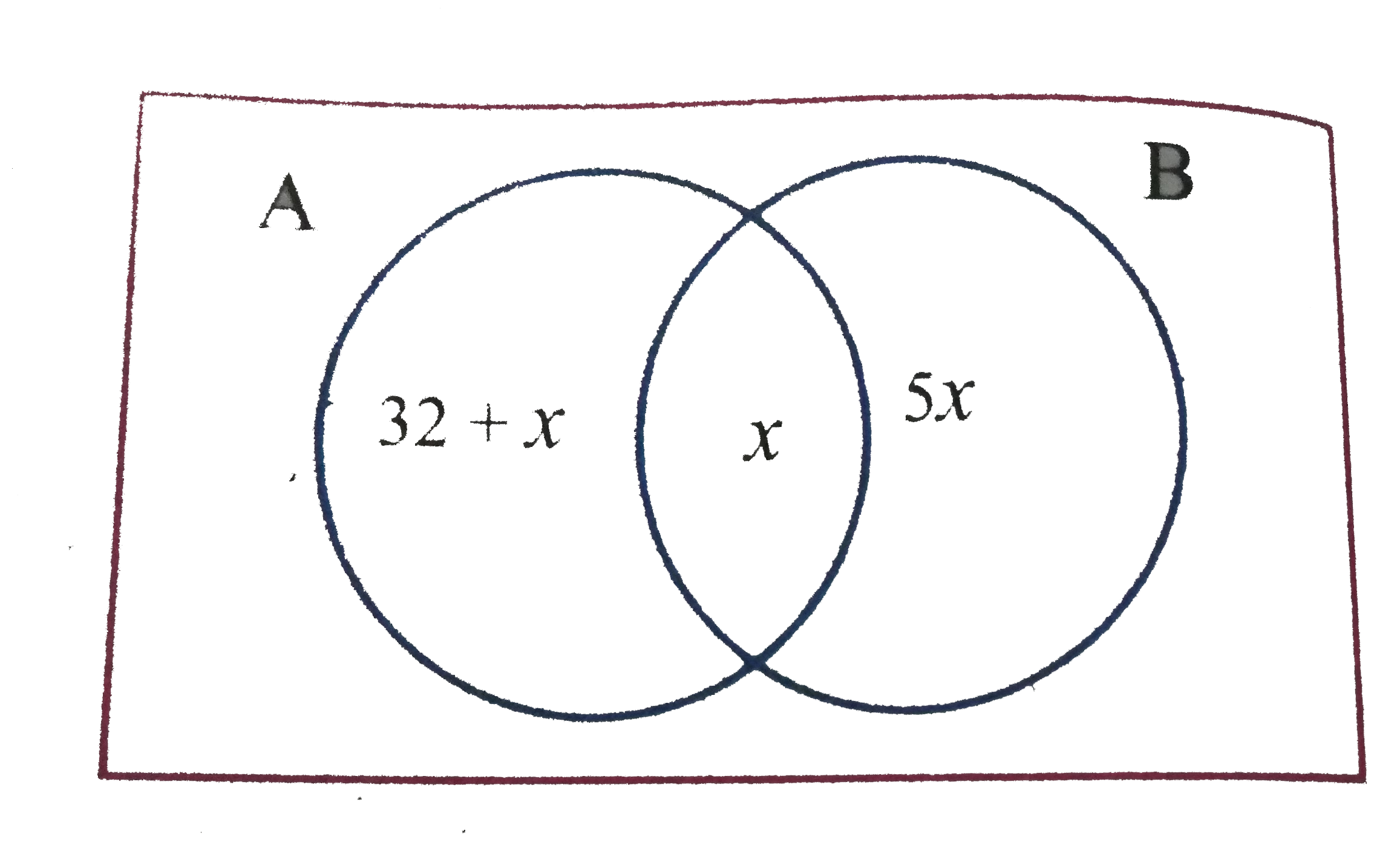
View SolutionA and B are two sets such that n(A - B) = 32 + x, n(B - A) = 5x and `n(AcapB)=x`. Illustrate the information by means of a venn diagram. Given that n(A) = n(B), calculate the value of x.
View SolutionOut of 500 car owners investigated, 400 owned car A and 200 owned car B, 50 owned both A and B cars. Is this data correct?
View SolutionIn a colony, 275 families buy Tamil newspaper, 150 families buy English newspaper, 45 families buy Hindi newspaper, 125 families buy Tamil and English newspapers, 17 families buy English and Hindi newspapers, 5 families buy Tamil and Hindi newspapers and 3 families buy all the three newspapers. If each family buy atleast one of these newspapers then find
(i) Number of families buy only one newspaper
(ii) Number of families buy atleast two newspapers
(iii) Total number of families in the colony.
View SolutionA survey of 1000 farmers found that 600 grew paddy, 350 grew ragi, 280 grew corn, 120 grew paddy and ragi, 100 grew ragi and corn, 80 grew paddy and corn. If each farmer grew atleast any one of the above three, then find the number of farmers who grew all the three.
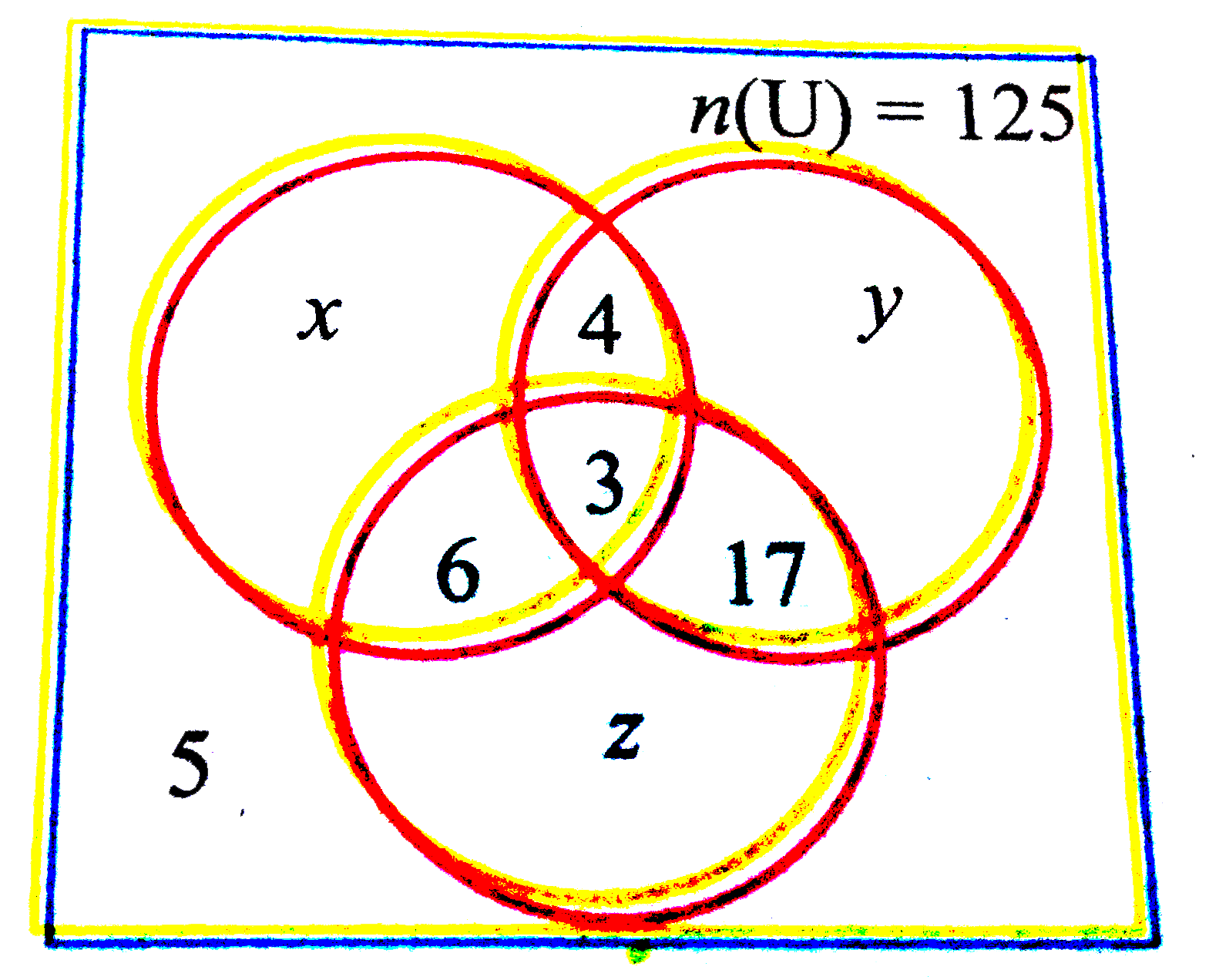
View SolutionIn the adjacent diagram, if n(U) = 125, y is two times of x and z is 10 more than x, then find the value of x, y and z.
View SolutionEach student in a class of 35 plays atleast one game among chess, carrom and table tennis. 22 play chess, 21 play carrom, 15 play table tennis, 10 play chess and table tennis, 8 play carrom and table tennis and 6 play all the three games. Find the number of students who play (i) chess and carrom but not table tennis (ii) only chess (iii) only carrom (Hint: Use Venn diagram)
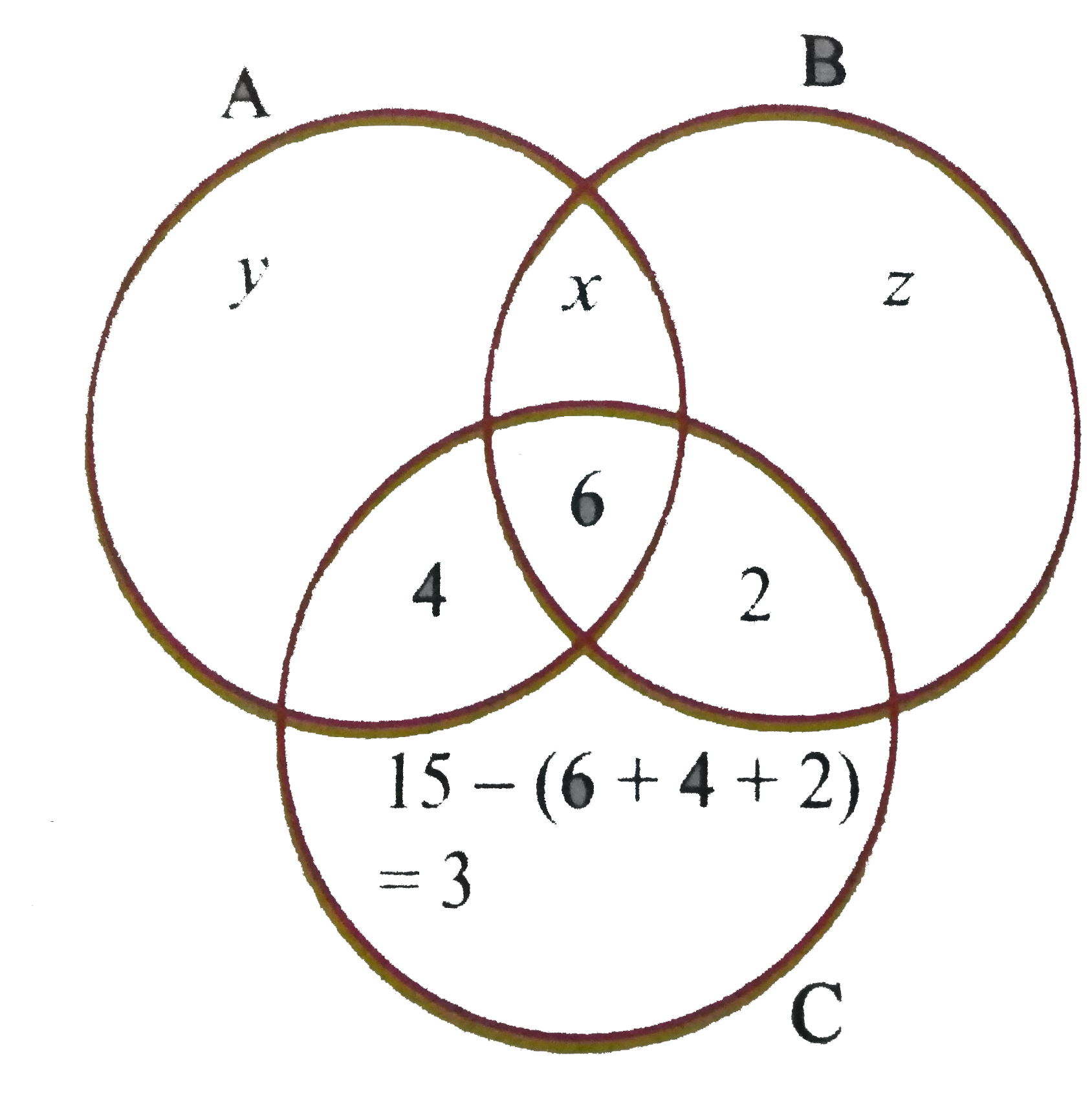
View SolutionIn a class of 50 students, each one come to school by bus or by bicycle or on foot. 25 by bus, 20 by bicycle, 30 on foot and 10 students by all the three. Now how many students come to school exactly by two modes of transport?
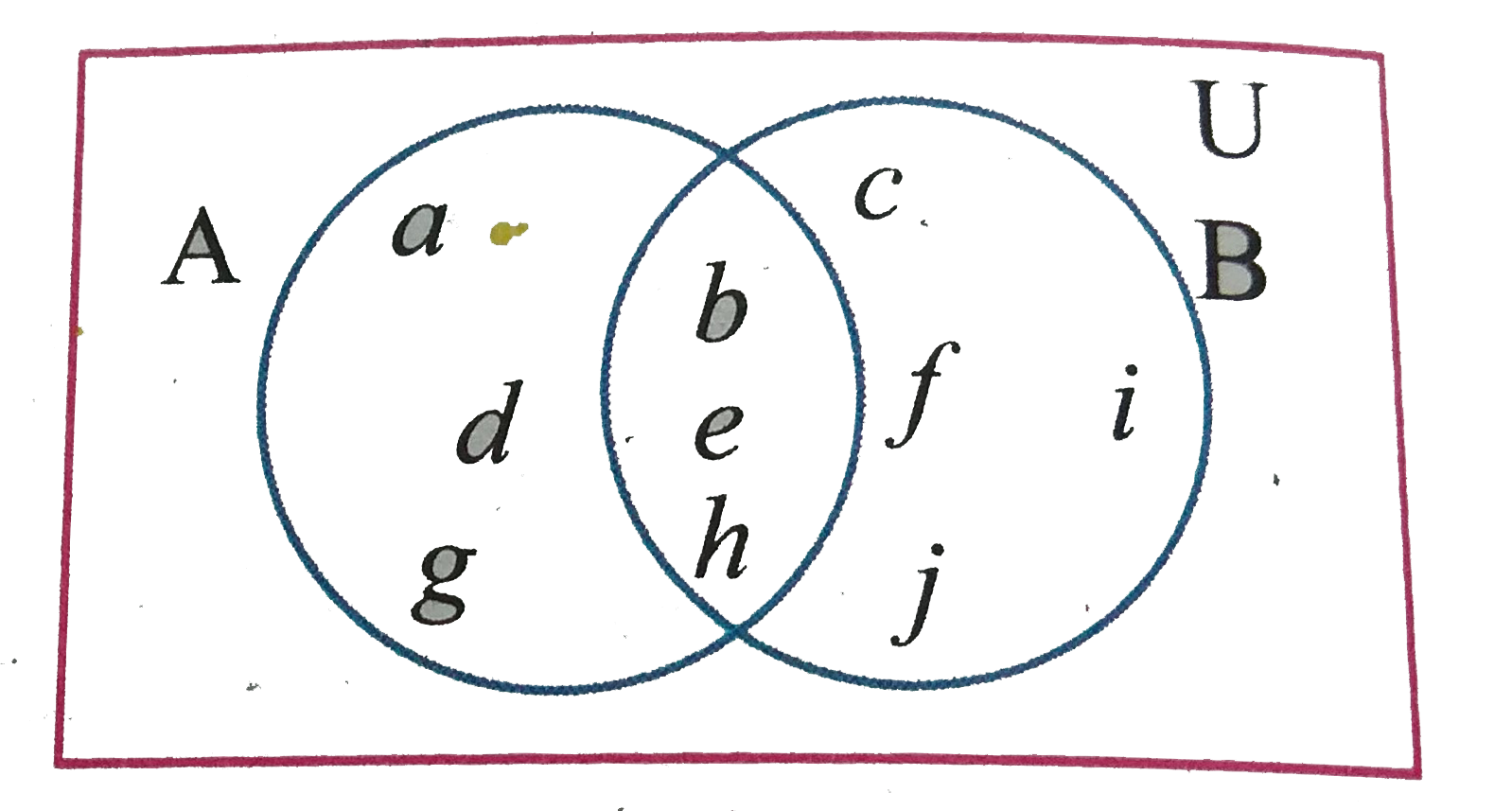
View SolutionFrom the given venn diagram. Find (i) A, (ii) B, (iii) `AcupB`, (iv) `AcapB` also verify that `n(AcupB)=n(A)+n(B)-n(AcapB)`
View SolutionIf n(A) = 12, n(B) = 17 and `n(AcupB)=21" find "n(AcapB)`.
View SolutionIn a school, 80 students like Maths, 90 students like Science, 82 students like History, 21 like both Maths and Science, 19 like both Science and History 20 like both Maths and History and 8 liked all the three subjects. If each student like atleast one subject, then find (i) the number of students in the school (ii) the number of students who like only one subject.
View SolutionState the formula to find `n(AcupBcupC)`.
View SolutionVerify `n(AcupBcupC)=n(A)+n(B)+n(C)-n(AcapB)-n(BcapC)-n(AcapC)+n(AcapBcapC)` for the following sets A = {1, 3, 5, 6, 8}, B = {3, 4, 5, 6) and C = {1, 2, 3, 6}
View Solution
EXERCISE 1.6 questions and complete solutions for chapter SET LANGUAGE of SURA MATHS (TAMIL ENGLISH) of Class 9