Complete Solutions to Question bank of chapter SIMILAR TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | SIMILAR TRIANGLES |
| V PUBLICATION | Question bank |
| Number Of Questions | 46 |
| Academic Year | 2023-24 |
The perpendicular from the square corner of a triangle cuts the Opposite side into two parts of 2 and 3 centimetres length.'(##VPU_HSS_MAT_IX_C07_E01_001_Q01##)'
i) Prove that the two small triangles cut by the perpendictlar have the same angles.
ii) Taking the length-of the perpendicular as 'h', prove that 'h2=3~h'.
iii) Calculate-the perpendicular sides the large triangle.
in) Prove that if the perpendicular from the square comer of a triangle divided the opposite side into parts of lengths a and 'mathbffb' and if the length of the perpendicular is 'h', then 'h^2=' ab.05:06View SolutionAt two ends of a horizontal line, angles of equal size are. drawn, and some points on the slanted lines are joined:'(##VPU_HSS_MAT_IX_C07_E01_002_Q01##)'
i) Prove that the parts of the horizontal line and parts of the slanted line are in, the same ratio.
ii) Prove that the two slanted lines at the ends of the horizontal line are also in the same ratio.
iii) Explain how a line of length 6 centimetres can be divided in the ratio '3: 4' using this.05:14View SolutionThe midpoint of the bottom side a square is joined to the ends of the top side and extended by the same length. The ends of these lines are joined and perpendiculars are drawn from these points to the bottom side of the square extended:'(##VPU_HSS_MAT_IX_C07_E01_003_Q01##)'
a) Prove that the rilateral obtained thus is also a square.
b) Explain how we can draw a square with two corners on the dlaineter and the others on a sëmicircle, as shown in the picture.05:38View SolutionThe picture shows a square drawn sharing one corner with a triangle and the other three corners on'the sides of this triangle.'(##VPU_HSS_MAT_IX_C07_E01_004_Q01##)'
I) Calculate the length of a.side' of the square.
ii) What. is the length of a side. of the square drawn like this within a triangle of sides 3, 4 and 5 centimetres?01:46View SolutionTwo poles of heights 3 metres and 2 metres are erected up on thè ground and ropes are stretched from the top of each to the foot of the other.'(##VPU_HSS_MAT_IX_C07_E01_005_Q01##)'
i)' At what height above the ground do the ropes cross each other?
ii) Prove that this height would be the same, whatever be the distance between the poles.
ii) Taking the heights of the poles as a and 'mathbffb' and height above the ground of the point where the ropes cross each other, as,'h', find the relation between 'mathbffa, underlineb' and 'h'.01:35View SolutionIn the figure, 'A P' and 'B Q' are perpendicular to 'A B'. Suppose that 'A P=4 ~cm' and 'B Q=2 ~cm'. Prove that 'A C: C B=2: 1''(##VPU_HSS_MAT_IX_C07_E01_006_Q01##)'
03:58View SolutionA boy '1.2' metres tall stands 1 metre away from the foot of a lamp post. If the length of his shadow is '1.5' metres, what is the height of the lamp post?
03:53View SolutionProve that PR = 2 QS.'(##VPU_HSS_MAT_IX_C07_E01_008_Q01##)'
02:21View Solutiona) Find the measures of the angles of triangleAPB and. 'triangle APC'.
b) What is the relation between the sides?
c) Prove that 'P B xx P C=P A^2'.'(##VPU_HSS_MAT_IX_C07_E01_009_Q01##)'04:05View SolutionIn the figure 'angle A D B=angle B C E' Prove that 'AB xx AC=AD xx AE''(##VPU_HSS_MAT_IX_C07_E01_010_Q01##)'
07:13View SolutionIn the figure, 'angle A D B=angle B C D'. Prove that 'A B xx A C=A D^2''(##VPU_HSS_MAT_IX_C07_E01_011_Q01##)'
04:58View SolutionIn the figure, 'angle A=angle D'. Prove that 'PA xx PB=PC xx PD'.'(##VPU_HSS_MAT_IX_C07_E01_012_Q01##)'
02:49View SolutionDraw a triangle of angles the same as those of tho triangle shown and sides scaled by '1 14'.'(##VPU_HSS_MAT_IX_C07_E02_001_Q01##)'
02:02View SolutionSee this picture of a rilateral.
1) Draw a rilateral with angles the same as those of this one and sides scaled by '1 12'
2) Draw a rilateral with angles different from those of this and sides scaled by '1 12''(##VPU_HSS_MAT_IX_C07_E02_002_Q01##)'02:04View SolutionDraw a rilateral with angles the same as those of this one and the sides scaled by '1 12''(##VPU_HSS_MAT_IX_C07_E02_003_Q01_Q01##)'
02:04View SolutionThe picture shows two circles with the same centre and two triangles formed by joining the centre to the. points of Intersection of the circles with two radii of the larger circle:
'(##VPU_HSS_MAT_IX_C07_E03_001_Q01##)' Prove that these 'triangles are similar.03:31View SolutionThe lines joining the circumcentre of a triangle to the vertices are extended to meet another circle with the same centre, and these points are joined to make another triangle.
'(##VPU_HSS_MAT_IX_C07_E03_002_Q01##)' i) Prove that the twò triangles are similar,
ii). Prove that the scale factor of the sides of the triangle is the scale factor of the rạdii of the circles.03:11View SolutionÀ point inside a rilateral is joined.to its vertices and the lines are extended by the same scale factor. Their ends are joined to make another rilateral.
'(##VPU_HSS_MAT_IX_C07_E03_003_Q01##)' i). Prove that the sides of the two rilaterals are scaled by the same factor.
ii) Prove that the angles of the two quađrilaterals are the same.03:24View SolutionTriangle ABC' and 'triangle PQR' 'are similar triangles. If 'AB=6 cm, BC=7 cm, PQ=9 cm','PR=6 cm', find other sides of the triangles.
02:48View SolutionIn the figure 'A D' is parallel to 'B D' and 'A B' is parallel to DE. Prove that 'triangle A B C' and 'triangle E D' A are similar triangles.'(##VPU_HSS_MAT_IX_C07_E03_005_Q01##)'
02:26View SolutionIn 'triangle A B C, P' is any point in 'B C_i D, E, F' are midpoints of 'BP, AP', CP respectively. Prove.that 'triangle A B C' and 'triangle D E F' are similar.'(##VPU_HSS_MAT_IX_C07_E03_006_Q01##)'
01:28View SolutionIn the figure AB is parallel to PQ. BC is parallel to BR. Prove that 'A BB C= PQ QR '.
04:07View SolutionTriangle ABC' is a right angled triangle with 'angle B=90degree.' The altitude through B meets AC at D. Prove that the three triángles 'triangle ABC, triangle ADB, triangle BCD' 'are similar.
03:22View SolutionIn the figure 'B C'. is parallel to 'D E'. 'A B=6 ~cm, BD=3 ~cm'
a) '(##VPU_HSS_MAT_IX_C07_E04_001_Q##)'What is the length of AD? b) If 'BC=4 cm', what is DE?
(c) What is the ratio of the perimeters of the triangles 'ABC' and ADE?
d) 'cdot A B=5 ~cm_j AC^prime=4 ~cm, angle A=30^(circ) .' Draw the. triangle ABC and drạw a triangle whose periméter_is '11^1 /_2' xx the perimeter of ABC. '' (Annual 2019)03:00View SolutionIn the figure, 'angle dotA=angle P, angle B=angle Q_1, A B=9' centimetres, 'A C=10' centimetres, 'P R=' 20 centimetres,
a) What is the length of PQ?.
b) If the perimeter of triangle 'ABC' is 30 centimetres, what Is the perimeter of triangle PQR?
'(##VPU_HSS_MAT_IX_C07_E04_002_Q01##)' c) If area of triangle ABC is '30 sqrt2' square centimetres. What is the area of triangle 'beginarrayll PQR?01:32View SolutionIn the figure, 'O' is the centre of the circle. 'angle P=angle R=90^(circ), OP=2' centi- metres. PR = RB.
a) What is the measure of 'angle B ?'
b) What is the length of 'BC' ?
c) Find the length of 'Q R'. '(##VPU_HSS_MAT_IX_C07_E04_003_Q01##)'03:45View SolutionIn the figure, 'angle A B C=angle A P B=90^(circ) .'
a). How' many triangles are there in the figure? Which are they?
b) Prove that these triangles are similar.'(##VPU_HSS_MAT_IX_C07_E04_004_Q01##)'03:09View SolutionIn the figure 'angle B=angle D=90^(circ), angle B F E=65^(circ)'
a) What is the measure of 'angle D F C ?'
b) Prove that 'FE xx FC=FD xx FB' '(##VPU_HSS_MAT_IX_C07_E04_005##)'03:12View SolutionIn the figure 'angle dotB=angle D=angle E C A=90^(circ)' 'B C=D C=4' centimetres. 'E D=3' centimetres.
a) What is the length of EC?
b) If 'angle ECD=x_i' find 'angle ACB',
c) Find the lengths of AE.
d) 'CE: AC: AE=' mes '' '(##VPU_HSS_MAT_IX_C07_E04_006_Q01##)'02:00View Solution'A B' is the diameter of the circle. 'C D' is a chord perpendicular to 'AB, angle A=angle D'.
a) Write another pair of equal angles in the figure.
b) If 'P C=6' centimetres, what is the length of D?
c) Prove that 'PA cdot x PB=PC^2'
d) If 'P A=9' centimetres, 'P C=6' centimetres, what is the tength of 'PB' ? '(##VPU_HSS_MAT_IX_C07_E04_007_Q01##)'07:27View SolutionIn rilateral 'A B C D, A B=4' centimetres, 'BC=3' centimetres, 'CD=2' centimetres, 'A D=2' centimetres, 'A C=3' centimetres. Draw rilateral ABCD. Draw another riateral with same angles and sides two xx as that of ABCD. '(##VPU_HSS_MAT_IX_C07_E04_008_Q01##)'
02:18View SolutionIn the figure, 'angle A D B=angle B C D'. Prove that 'A B xx A C=A D^2'. '(##VPU_HSS_MAT_IX_C07_E04_009_Q01##)'
03:49View SolutionIn the figure
a) How many xx the sides of the large triangle is longer than fhat of the smali triangle?
b) Write the angles of two triangles which 'beginarrayll are equal. '(##VPU_HSS_MAT_IX_C07_E04_010_Q01##)'03:20View Solution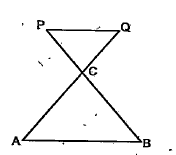
In the figure, the sides AC and BC are extended to the points 'Q' and 'P' respectively- If `angle A=angle P`
a) Write the equal angles of triangles ABC and 'PQC'.
b) Prové that `A C xx Q C=B C xx P C`06:49View SolutionIn the figure, the sides of triangle 'ABC' are 5 cenfinetres, 6 centimetres and the sides of trianglePQR are 10 cantimetre, 12 centimetres and 14 centimetres.
'(##VPU_HSS_MAT_IX_C07_E04_012_Q01##)'
a) If 'angle B=x^(circ)', find 'angle Q'.
b) The perpendicular from A to BC is AD and the perpendicular from 'P' to 'QR' is PS. Write the measures of angles of 'triangle ABD and PQS.
c) How mamy times of AD is PS?
d) How many tịmes the area of triangle 'A B C' is the area of friangle PQR?01:26View SolutionIn triangle 'ABC, angle B=90 degree and 'BD' is perpendicular to AC.
a) If 'angle A=x degree, write the angles of triangles 'ABD' 'and 'BDC'.
b) Prove that '(BD)^2=AD X CD'.04:49View SolutionIn the figure, the lines 'A B' and 'C D' Intersect at the point 'P'. Prove that length of 'PB' is a third of the length of AP.
'(##VPU_HSS_MAT_IX_C07_E04_014_Q01##)'03:04View SolutionIn the figure, the line 'D B' extended and the perpendicular to 'BC' at 'C' meets at E.
i) Prove that the triangles 'ADB' and 'CBE' have the same angles.
if) Compute the length of CE.
'(##VPU_HSS_MAT_IX_C07_E04_015_Q01##)'02:57View Solutiona)Find out the angles of the triangles APC and BPC in the figure.
'(##VPU_HSS_MAT_IX_C07_E04_016_Q01##)'
b) What is the relation between the sides of these triangles?
c) Prove that 'A P xx B P=C P^2'.02:20View SolutionPQR and XVZ are. angled triangles and 'O Q=8' centimetre.
1) Find- 'angle P' and 'angle X_i'.
2) If 'Y Z' is '1 12' xx of 'P Q', find all sides of " triangle XYZ. (Second term 2017)01:25View SolutionA point 'O' inside the hexagon ABCDEF is joined to its vertices and those line are extended '1_22^1' xx. Their ends are joined to make another hexagon PQRSTU.
'(##VPU_HSS_MAT_IX_C07_E04_018_Q01##)'
i) Prove that the angles of the two hexagons are same.
ii) Prove that the length of sides of the bigger hexagon is '1 12' times the length. of sides of the smaller hexagon.03:11View Solution(##VPU_HSS_MAT_IX_C07_E04_019_Q01##)'
a) Write the measure of 'angle A'.
b) Find the length of 'PQ'.02:37View SolutionProve that 'P R=2 Q S'
'(##VPU_HSS_MAT_IX_C07_E04_020_Q01##)'01:59View Solution(##VPU_HSS_MAT_IX_C07_E04_021_Q01##)'
In the figure 'P Q' is parallel to 'B C' and 'P R' is parallel to 'CD'.
a) Write, the equal angles of triangle 'AQP', and ABC.
b) Write the equal angles of triangles ARP and 'ADC'.
c) Prove that 'ARAD=AQAB'01:05View SolutionIn triangle 'ABC, angle B=90 degree . BD' is perpendicular to 'AC'.
a) If 'angle A=x degree', find the measures of 'angle C' and 'angle ABD'
b) Write the ratios of the sides opposite to the equal angles in triangle 'ABD' and triangle ABC.
c) Prove that 'AB^2=AD x AC'.04:37View SolutionIn the figure, 'ABC' is a triangle and 'PQRB' is a square. 'PA=12 cm' and 'R C=3 cm'. Find the area of the square.
'(##VPU_HSS_MAT_IX_C07_E04_023_Q01##)'02:12View Solution
Question bank questions and complete solutions for chapter SIMILAR TRIANGLES of V PUBLICATION of Class 9