Complete Solutions to Example of chapter త్రిభుజాలు of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | త్రిభుజాలు |
| VGS PUBLICATION-BRILLIANT(TELUGU) | Example |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
కింద కొన్ని ప్రవచనాలు ఇవ్వబడ్డాయి. అవి సత్యమో, కాదో సరిచూడుము. రెండు వృత్తములు ఎల్లప్పుడూ సర్వసామానం
View Solutionకింద కొన్ని ప్రవచనాలు ఇవ్వబడ్డాయి. అవి సత్యమో, కాదో సరిచూడుము. ఒకే పొడవు కలిగిన రెండు రేఖఖండములు ఎల్లప్పుడూ సర్వసమనం
View Solutionకింద కొన్ని ప్రవచనాలు ఇవ్వబడ్డాయి. అవి సత్యమో, కాదో సరిచూడుము. రెండు లంబకోణ త్రిభుజాములు కొన్నిసార్లు సర్వసమనము
View Solutionకింద కొన్ని ప్రవచనాలు ఇవ్వబడ్డాయి. అవి సత్యమో, కాదో సరిచూడుము. భుజాముల కొలతలు సమనముగాగల రెండు సమబాహు త్రిభుజాములు ఎల్లప్పుడూ సర్వసామానం
View Solutionఇచ్చిన పటములు సర్వసమనమో కాదో సరిచూచుటకు కావలసిన కనీస కొలతలు ఎన్ని? రెండు దీర్ఘచతురస్రాలు
View Solutionఇచ్చిన పటములు సర్వసమనమో కాదో సరిచూచుటకు కావలసిన కనీస కొలతలు ఎన్ని? రెండు సమచతుర్భుజములు
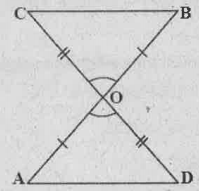
View Solutionఇచ్చిన పటంలో AB మరియు CD లు 'O' వద్ద ఖండించుకొనుచున్నాయి. OA=OB మరియు OD=OC అయిన `Delta AOD= Delta BOC`
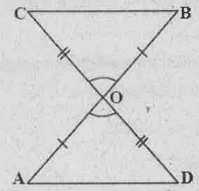
View Solutionఇచ్చిన పటంలో AB మరియు CD లు 'O' వద్ద ఖండించుకొనుచున్నాయి. OA=OB మరియు OD=OC అయిన `AD |\| BC` అని నిరూపించండి.
View SolutionAB ఒక రేఖఖండము సరళరేఖ l దీనికి లంబ సమద్విఖండన రేఖ . ఈ రేఖపై P ఒక బిందువు అయిన ఈ P బిందువు A,B బిందువుల నుండి సమాన దూరంలో ఉంటుందని చూపుము.
View Solutionఈ కింది త్రిభుజాములు సర్వసమనములు అవునో కాదో తెలుపుము. దానికి కారణములను వివరించుము .
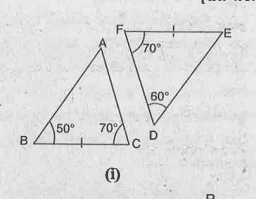
View Solutionఈ కింది త్రిభుజాములు సర్వసమనములు అవునో కాదో తెలుపుము. దానికి కారణములను వివరించుము .
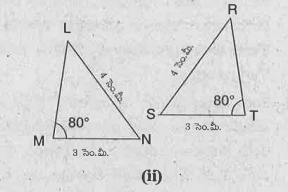
View Solutionఇచ్చిన పటంలో AB,DC రేఖఖండములను P బిందువు సమద్విఖండన చేసిన `Delta APC = Delta BPD` అని చూపుము.
<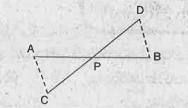
View Solutionఒక త్రిభుజాములోని రెండు కోణములు , వాటి మద్య భుజము వరుసగా వేరొక త్రిభుజాములోని రెండు కోణములు, వాటి మధ్య భుజామునకు సమానమైన ఆ రెండు త్రిభుజాములు సర్వసమనములు.
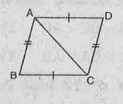
View Solutionపటంలో `Delta ABC ~= Delta CDA` అగుటకు నియమం
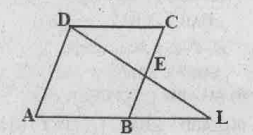
View Solutionఇచ్చిన పటంలో `AL |\| DC,BC` మధ్యబిందువు E అయిన `Delta EBL = Delta ECD`అని చూపుము.
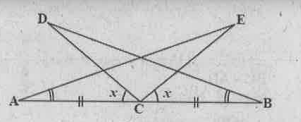
View Solutionకింది పటంలోని సమాచారమును ఉపయోగించుకుని `Delta DBC = Delta EAC`
View SolutionAB,CD లు సమంతారాలు. AD మధ్య బిందువు O అయిన BC కి కూడా మధ్య బిందువు O అని నిరూపించుము.
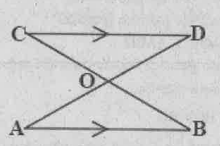
View SolutionAB,CD లు సమంతారాలు. AD మధ్య బిందువు O అయిన BC కి కూడా మధ్య బిందువు O అని నిరూపించుము.

View Solutionఒక త్రిభుజాములో సమాన కొనలకు ఎదురుగా ఉండే భుజాలు సమానము.,
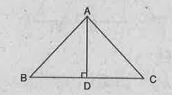
View Solution`Delta ABC`లో AD అనేది BC భుజామునకు లంబ సమద్విఖండన రేఖ. `Delta ABC`, AB=AC అయ్యేటట్లున్న సమద్విబహు త్రిభుజామని చూపండి.
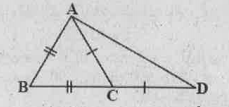
View Solutionఇచ్చిన పటంలో AB=AC మరియు AC=CD. అయిన `/_BAD : /_ADB = 3:1` అని చూపండి.
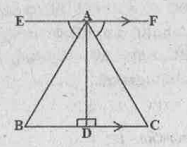
View Solutionఇచ్చిన పటంలో AD అనేది BC మరియు EF లు రెండింటికీ లంబము. ఇంకా `/_EAB = /_FAC`, అయిన `Delta ABD మరియు Delta ACD` లు సర్వసమనమని చూపుము . ఇంకా `AB=2x+3,AC =3y+1`, BD =x మరియు DC = y+1 అయిన x,y విలువలు కనుగొనండి.
View Solution`Delta ABC` లో సమాన భుజాలు AB, AC ల మధ్య బిందువులు వరుసగా E మరియు F , BF = CE అని చూపండి.
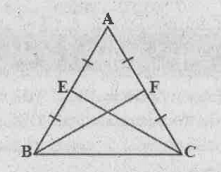
View Solutionఒక సమద్విబహు త్రిభుజము ABC లో AB=AC , D మరియు E బిందవులు BC పై BE=CD అయ్యేటట్లున్న బిందువులు అయిన AD=AE అని చూపండి.
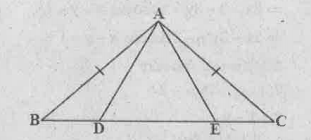
View Solution(లం. క. భు. సర్వసమానత్వ నియమం.) : రెండు లంబకోణ త్రిభుజాములలో ఒక త్రిభూజములోని కర్ణము, భుజాములు వరుసగా రెండవ త్రిభుజాములోని కర్ణము, భుజాములకు సమానమైన ఆ రెండు త్రిభుజాములు సర్వసమాన త్రిభుజాములు. లం. క. భు. అనగా లంబకోణము-కర్ణము-భుజము. ఇప్పడూ నిరూపణ చేద్దాం.
View SolutionAB ఒక రేఖఖండము. P మరియు Q అనే బిందువులు AB కి రెండు వైపులలో A,B లకు సమానదూరంలో ఉన్నాయి. అయిన PQ రేఖ AB కి లంబసమద్విఖండన రేఖ అని చూపండి.
View Solutionl,m రేఖలు A బిందువు వద్ద ఖండించుకొంటున్నాయి. P బిందువు ఈ రేఖలకు సమాన దూరంలో ఉంది. AP రేఖ l,m ల మధ్య ఏర్పడిన కోణాన్ని సమద్విఖండన చేస్తుందని చూపండి.
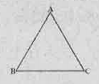
View Solutionఒక సమబాహు త్రిభుజాములో ప్రతి కోణము `60^@` అని చూపండి.
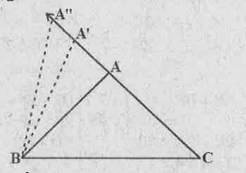
View SolutionABC త్రిభుజాన్ని గీసి CA ని A బిందువు వరకు పొడిగించండి. కావున `A^(')C>AC, A^('),B` లను కలిపి త్రిభుజము `A^(')BC` ని ఏర్పరచండి. ఇప్పుడు మీరు `/_A^(')BC `మరియు `/_ABC` గురించి ఏమి చెప్పగలరు? ఆ రెండు కోణములను పొలచండి. మీరు ఏమి గమనించారు? స్పస్టంగా , `/_A^(')BC > /_ABC`
View Solutionఒక విషమబహు త్రిభుజాన్ని నిర్మించుము. భుజాల పొడవులను కొలవండి.
View Solutionఒక త్రిభుజాములో రెండు భుజాములు అసమనముగా నున్న పెద్ద భుజానికి ఎదురుగానున్న కోణము పెద్దది.
View SolutionAB రేఖఖండమును గీయుము. A కేంద్రంగా కొంత వ్యాసార్థముతో చపమును గీసి దానిపై వేర్వేరు బిందువులు P,Q,R,S,T లను గుర్తించుము. ఈ బిందువులన్నింటిని A,B బిందువులతో కలుపుము . మనం P బిందువు నుండి T బిందువు వైపు కదులుతున్నప్పుడు `/_A` క్రమంగా పెద్దదవుతుంది. దానికి ఎదురుగా ఉండే భుజం కొలత ఎలా ఉంటుంది. దాని ఎదురుగా ఉండే భుజం కొలత కూడా పెరుగుతూ ఉండడాన్ని గమనించవచ్చును. అనగా `/_TAB > /_SAB > /_RAB > /_QAB > /_PAB` మరియు `TB>SB>RB>QB>PB.`
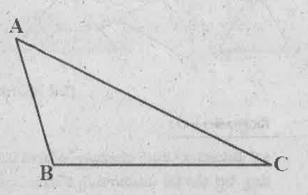
View Solutionఇప్పుడు వేర్వేరు కోణముల కొలతలు గల ఒక త్రిభుజామును గీయుము. భుజాల పొడవులను కొలుచుము. పెద్ద కోణానికి ఎదురుగవున్న భుజము పొడవుగా ఉండడాన్ని గమనించవచ్చును. పటంలో పెద్ద కోణము `/_B` మరియు దాని ఎదురుగానున్న పొడవైన భుజము AC. ఈ కృత్యమును వివిధ త్రిభుజాములతో చేయుము . పై సిద్దాంతము విపర్యాయము సరియమని గ్రహిస్తాము
View Solutionకింద ఇవ్వబడిన ప్రతి త్రిభుజం యొక్క కోణాలను, భుజాల పొడవులను కొలవండి. ప్రతి త్రిభుజంలోని ఒక్కొక్క భుజామునకు మరియు వాటి ఎదురుగానున్న కొనలకు మధ్యగాల సంభందం ఏమై ఉంటుందనుకొంటున్నారు?
 ,
,  ,
, 
View Solutionఒక త్రిభుజాములో పెద్ద కోణానికి ఎదురుగానున్న భుజము పొడవైనది.
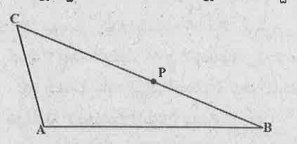
View Solutionత్రిభుజము ABC గీసి వాటి భుజాల పొడవులు కొలవండి. దానిలో AB+BC, BC +AC మరియు AC +AB లను కనుగొని వాటి మూడు భుజాలతో పొలచండి. మీరు ఏమి గమణిస్తారు? ఈ కృత్యమును వివిధ త్రిభుజాములను తిశకుకుని చేయండి.
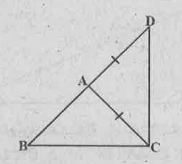
View Solutionఒక త్రిభుజాములో ఏవైనా రెండు భుజాల పొడవుల మొత్తము 3 వ భుజము పొడవుకన్న ఎక్కువ. కింది పటంలో `Delta ABC` లో AD =AC అగునట్లు భుజము BA బిందువు D వద్దకు పొడిగించబడినది. `/_BCD > /_BDC` అని `BA+AC > BC? ` అని మీరు చూపించగలరా?
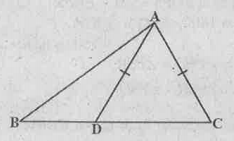
View Solution`Delta ABC` లో AD=AC అగునట్లు భుజం BC పై D ఒక బిందువు అయిన `AB > AD` అని చూపండి.
View Solution
Example questions and complete solutions for chapter త్రిభుజాలు of VGS MATHS (TELUGU) of Class 9