Complete Solutions to Exercise of chapter త్రిభుజాలు of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | త్రిభుజాలు |
| VGS PUBLICATION-BRILLIANT(TELUGU) | Exercise |
| Number Of Questions | 89 |
| Academic Year | 2023-24 |
చతుర్భుజం ABCD లో , AC=AD మరియి `/_A` కు AB కోన సమద్విఖండన రేఖ అయిన `Delta ABC = Delta ABD` అని చూపండి. BC మరియు BD ల గురించి మీరు ఏమి చెప్పగలరు?
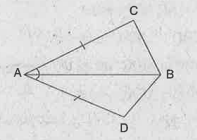
View SolutionABCD చతుర్భుజంలో AD=BC మరియు `/_DAB = /_CBA` అయిన `Delta ABD ~= Delta BAC`
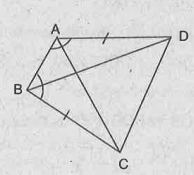
View SolutionABCD చతుర్భుజంలో AD=BC మరియు `/_DAB = /_CBA` అయిన BD=AC
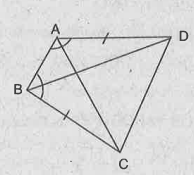
View SolutionABCD చతుర్భుజంలో AD=BC మరియు `/_DAB = /_CBA` అయిన `/_ABD = /_BAC` అని నిరూపించుము.
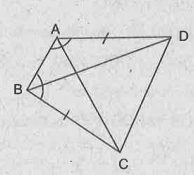
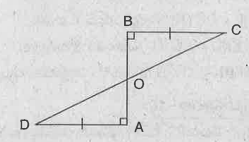
View SolutionAD,BC లు సమానము మరియు రేఖఖండము AB కి లంబములు, అయిన CD రేఖఖండము AB ని సమద్విఖండన చేయునని చూపుము.
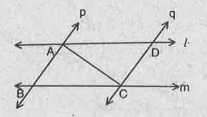
View Solutionl,m అనే ఒక జత సమాంతర రేఖలు p మరియు q అనే వేరొక జత సమాంతర రేఖలచే ఖండించబడినవి. అయిన `Delta ABC ~= Delta CDA`అని నిరూపించుము.
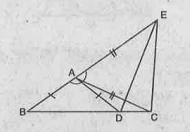
View Solutionక్రింది పటంలో AC=AE,AB=AD మరియు `/_BAD=/_EAC` అయిన BC=DE అని నిరూపించుము.
View Solutionలంబకోన త్రిభుజము ABC లో లంబకోణము C వద్ద ఉన్నది. కర్ణము AB యొక్క మధ్యబిందువు. M. C బిందువు M కు కలిపి DM=CM అగునట్లు D బిందువు వద్దకు పొడిగించినవారు. పటంలో చూపినట్లు D బిందువును B బిందువుకు కలిపినరు. అయిన క్రింది వాటిని నిరూపించండి. `Delta AMC ~= Delta BMD`
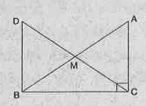
View Solutionలంబకోన త్రిభుజము ABC లో లంబకోణము C వద్ద ఉన్నది. కర్ణము AB యొక్క మధ్యబిందువు. M. C బిందువు M కు కలిపి DM=CM అగునట్లు D బిందువు వద్దకు పొడిగించినవారు. పటంలో చూపినట్లు D బిందువును B బిందువుకు కలిపినరు. అయిన క్రింది వాటిని నిరూపించండి. `/_DBC` ఒక లంబకోణము
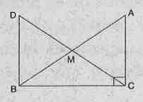
View Solutionలంబకోన త్రిభుజము ABC లో లంబకోణము C వద్ద ఉన్నది. కర్ణము AB యొక్క మధ్యబిందువు. M. C బిందువు M కు కలిపి DM=CM అగునట్లు D బిందువు వద్దకు పొడిగించినవారు. పటంలో చూపినట్లు D బిందువును B బిందువుకు కలిపినరు. అయిన క్రింది వాటిని నిరూపించండి. `Delta AMC ~= Delta BMD`

View Solutionలంబకోన త్రిభుజము ABC లో లంబకోణము C వద్ద ఉన్నది. కర్ణము AB యొక్క మధ్యబిందువు. M. C బిందువు M కు కలిపి DM=CM అగునట్లు D బిందువు వద్దకు పొడిగించినవారు. పటంలో చూపినట్లు D బిందువును B బిందువుకు కలిపినరు. అయిన క్రింది వాటిని నిరూపించండి. ``CM = 1/2 AB
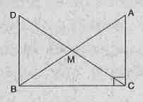
View Solutionక్రింది పటంలో ABCD ఒక చతురస్రము మరియు `Delta APB` ఒక సమబాహు త్రిభుజము అయిన `Delta APD ~= Delta BPC`అని నిరూపించుము. (సూచన:`Delta APD Delta BPC` లలో `bar AD = bar BC, bar AP = bar BP` మరియు `/_PAD = /_PBC = 90^@ -60^@=30^@`)
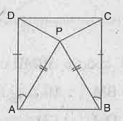
View Solutionక్రింది పటంలో AB = AC కావున `Delta ABC` ఒక సమద్విబహు త్రిభుజము BA మరియు `bar CA` లను `bar AQ = bar AP` అగునట్లు Q,P బిందువుల వద్దకు పొడిగించిన `bar PB bar QC` అని నిరూపించుము.
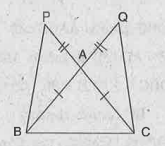
View Solutionక్రింది పటంలో `Delta ABC` లో BC మధ్య బిందువు D . `DE_|_AB,DF_|_AC`మరియు DE=DF అయిన `Delta BED ~= Delta CFD` అని నిరూపించుము.
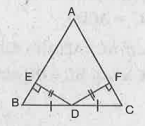
View Solutionఒక త్రిభుజాములో ఒక కోణం యొక్క కోన సమద్విఖండనరేఖ ఎదుటి భుజాన్ని కూడా సమద్విఖండన చేసిన ఆ త్రిభుజము సమద్విబహు త్రిభుజమని చూపుము.
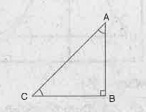
View Solutionఇచ్చిన పటంలో ABC ఒక లంబకోణ త్రిభుజము. లంబకోణము శీర్షము B వద్ద కలదు మరియు `/_BCA = 2 /_BAC` అయిన కారణము AC=2 BC అని చూపుము.
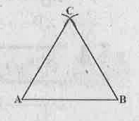
View Solutionవృత్తాలేకిని ఊపయోగించి త్రిభుజామును నిర్మించుటకు, ఏదేని కొంత కొలతతో రేఖఖండము AB ని గీయుము. వృత్తాలేఖిని తీసుకొని దానికి సరిపడినంత కొలత తీసుకొని బిందువులు A,B ల వద్ద ఉంచి చపములు గీయుము. అప్పుడు మీకు ఎ రకమైన త్రిభుజము ఏర్పడుతుంది.? అపుడు ఏర్పడినది ఒక సమద్విబహు త్రిభుజము. అందువలన పటంలోని `Delta ABC,AC=BC` కలిగిన ఒక సమద్విబహు త్రిభుజము. ఇప్పుడు కోణములు `/_A, /_B` ల విలువలను కొలవండి. మీరు ఏమి గమనిస్తారు?
 ,
,  ,
, 
View Solutionఒక సమద్విబహు త్రిభుజామును కత్తిరించుము. సర్వసమాన భాగములు ఒకదానిపై ఒకటి ఏకీభవించునట్లు ఆ త్రిభుజామును మాడవండి. `/_A,/_B` ల గురించి మీరు ఏమి గమనించారు? అటువంటి ప్రతి త్రిభుజాములో, సమాన భుజాములకు ఎదురుగా ఉండే కోణములు సమానంగా ఉండడాన్ని మీరు గమనిస్తారు.
View Solutionఒక సమద్విబహు త్రిభుజాములో సమానభుజాములకు ఎదురుగానున్న కోణములు సమానము.
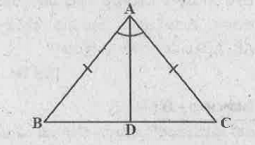
View Solutionసమద్విబహు త్రిభుజము ABC లో AB=AC,`/_B, /_C` ల కోన సమద్విఖండన రేకలు 'O' బిందువు వద్ద ఖండించుకొంటాయి. A మరియు O బిందువులను కలపండి. OB=OC
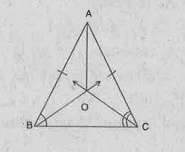
View Solutionసమద్విబహు త్రిభుజము ABC లో AB=AC,`/_B, /_C` ల కోన సమద్విఖండన రేకలు 'O' బిందువు వద్ద ఖండించుకొంటాయి. A మరియు O బిందువులను కలపండి. AO, `/_A` కు కోన సమద్విఖండన రేఖ.
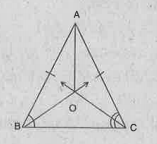
View Solution`Delta ABC`లో AD అనేది BC భుజామునకు లంబ సమద్విఖండన రేఖ. `Delta ABC`, AB=AC అయ్యేటట్లున్న సమద్విబహు త్రిభుజామని చూపండి.
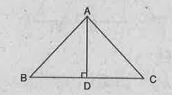
View Solution`Delta ABC` ఒక సమద్విబహు త్రిభుజము. సమాన భుజాలు AC,AB లకు గీసిన లంబాలు వరుసగా BE మరియు CF అయిన ఈ లంబాలు సమానమని చూపండి.
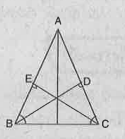
View Solution`Delta ABC` లో AC,AB భుజాలకు గీసిన లంబాలు BE,CF లు సమానము అయిన `Delta ABD ~= Delta ACE`
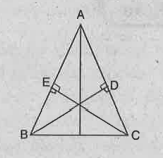
View Solution`Delta ABC` లో AC,AB భుజాలకు గీసిన లంబాలు BE,CF లు సమానము అయిన AB =AC అనగా `Delta ABC` ఒక సమద్విబహు త్రిభుజామని చూపండి.
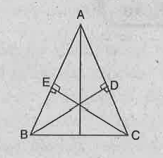
View Solution`Delta ABC, Delta DBC` లు ఒకే భుజము BC పై ఉన్న రెండు సమద్విబహు త్రిభుజాములు అయిన `/_ABD = /_ ACD` అని చూపండి.
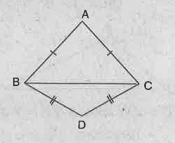
View Solution(భు. భు. భు. సర్వసామానత్వ నియమం) : నిర్మాణముల ద్వారా భు. భు. భు. సర్వసమానత్వ నియమము వర్తిస్తుంది. భు. భు. భు. సర్వసమానత్వ నియమం నిరూపణ.
View SolutionABCD చతుర్భుజములో AB=CD, BC =AD అయిన `Delta ABC ~= Delta CDA` అని నిరూపించండి.
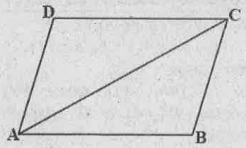
View Solutionకింది పటంలో `Delta ABC` మరియు `Delta DBC` లు `bar AB = bar BD` మరియు `bar AC = bar CD` అయ్యేటట్లున్న రెండు త్రిభుజాములు అయిన `Delta ABC ~= Delta DBC` అని చూపండి.
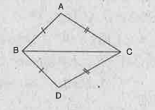
View Solutionఒక సమద్విబహు త్రిభుజము ABC లో AB=AC ,AD అనేది A నుండి BC కి గీసిన లంబము అయిన BC భుజాన్ని AD సమద్విఖండన చేయునని
View Solutionఒక సమద్విబహు త్రిభుజము ABC లో AB=AC ,AD అనేది A నుండి BC కి గీసిన లంబము అయిన `/_A` ని AD కోన సమద్విఖండన చేయునని చూపండి.
View Solution`Delta ABC ` లో రెండు భుజాములు AB,BC మరియు మధ్యగతం AM వరుసగా `Delta PQR` లో రెండు భుజాములు PQ,QR లు మరియు మధ్యగటం PN కు సమానము . అయిన ` Delta ABM ~= Delta PQN`
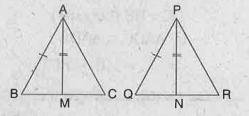
View Solution`Delta ABC ` లో రెండు భుజాములు AB,BC మరియు మధ్యగతం AM వరుసగా `Delta PQR` లో రెండు భుజాములు PQ,QR లు మరియు మధ్యగటం PN కు సమానము . అయిన ` Delta ABC ~= Delta PQR` అని చూపండి.
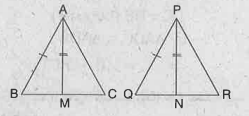
View Solution`Delta ABC` లో AC,AB భుజాలకు గీసిన లంబాలు BE,CF లు సమానము అయిన AB =AC అనగా `Delta ABC` ఒక సమద్విబహు త్రిభుజామని చూపండి.

View Solutionఒక సమద్విబహు త్రిభుజము ABC లో AB=AC అయిన `/_B = /_C` అని నిరూపించండి.
View Solutionఒక సమద్విబహు త్రిభుజము ABC లో AB=AC . AD=AB అగునట్లు భుజము BA ని D బిందువు వద్దకు పొడిగించినరు. `/_BCD` ఒక లంబకోణమని చూపండి.
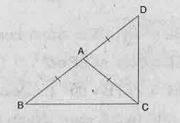
View Solution`Delta ABC` ఒక లంబకోణ త్రిభుజము. దీనిలో `/_A=90^@` మరియు AB=AC అయిన `/_B=/_C` అని చూపండి.
View Solutionఒక లంబకోణ త్రిభుజాములో కర్ణము అతి పొడవైన భుజమని నిరూపించండి.
View Solutionకింది పటంలో `Delta ABC ` లో భుజాలు AB,AC లు వరుసగా P,Q బిందువులకు పొడిగించబడినవి. ఇంకనూ `/_PBC < /_QCB`. అయిన AC >AB అని చూపండి.
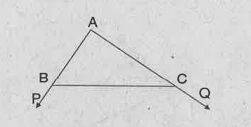
View Solutionకింది పటంలో `/_B < /_A` మరియు `/_C< /_D` అయిన `/_AD < /_BC` అని చూపండి.
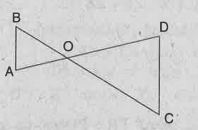
View Solutionచతుర్భుజము ABCD లో AB అతి చిన్న భుజం మరియు CD అతి పొడవైన భుజం . అయిన `/_A > /_C` మరియు `/_B>/_D` అని చూపండి.
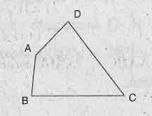
View Solutionక్రింది పటంలో `PR>PQ` మరియు `/_QPR` కోన సమద్విఖండన రేఖ PS అయిన `/_PSR > /_PSQ` అని చూపండి.
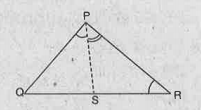
View Solutionఒక త్రిభుజము రెండు భుజాల కొలతలు 4 సెంమీ. మరియు 6 సెంమీ . అయిన 3 వ భుజం కోలాటగా ఉండడానికి సాధ్యమయ్యే అన్నీ ధనాత్మక పూర్ణ సంఖ్యల విలువలు కనుగొనండి. అటువంటి ఎన్ని త్రిభుజాలు సాధ్యమవుతాయి?
View Solution5 సెంమీ. 8 సెంమీ. 1 సెంమీ. కొలతతో ఒక త్రిభుజాన్ని నిర్మించడానికి ప్రయటనీచండి. ఈ నిర్మాణం సాధ్యమా?కదా?మీ వివరణను రాయండి.
View Solution`Delta ABC` సమద్విబహు త్రిభుజంలో AB=AC,AD ఒక ఉన్నతి, `/_BAD =50^@` అయిన `/_CAD`=
View Solution`Delta ABC ~= Delta LKM, Delta ABC` లోని AC భుజము, `Delta LKM` లోని దీనికి సమానము
View Solution`Delta ABC ~= Delta ACB` అయిన `Delta ABC` ఒక సమద్విబహు త్రిభుజము అయి ___అగును
View SolutionABC మరియు PQR త్రిభుజాలలో 3 భాగాలకు సంబంధించిన తుల్య సంబంధాలను ఇవ్వడమైనది. AB=QP,`/_B=/_P` మరియు BC=PR అయిన ఎ సరూపకత పై నియమాలను తృప్తిపరచును.
View Solution`Delta PQR ~= Delta EFD` అయిన ED=
View Solutionకింది వాటిలో సర్వసమానతను సూచించండి అంశము
View Solution`Delta ABC` భుజాలు BC,CA మరియు AB ల మధ్య బిందువులు D,E,F లయిన `Delta DEF` సర్వసమనమగును.
View Solution`Delta PQR ~= Delta EFD` అయిన ED=
View Solution`Delta PQR ~= Delta EFD` అయిన `/_E`=
View Solution`Delta ABC` లో AB=AC మరియు BC ని D దాకా పొడిగించిన `/_ACD=100^@` అయిన `/_A`=
View Solution`Delta PQR ~= Delta ABC` అయిన `/_R` =
View Solutionపటంలో `Delta ABC ~= Delta CDA` అగుటకు నియమం
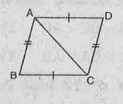
View Solutionపటంలో PQ=RS లు 'O' వద్ద ఖండించుచున్న `Delta POR ~= Delta QOS` అగుటకు నియమం
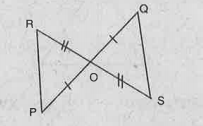
View Solution`Delta PQR` ఒక సమద్విబహు త్రిభుజంలో `bar QR` యొక్క మద్య బిందువు 'S' అయిన `Delta PQS ~=`
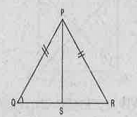
View Solutionపటంలో `bar XY` అనునది `bar PQ` కు లంబ సమద్విఖండన రేఖాయిన `Delta POX ~=Delta QOX` అగుటకు నియమము
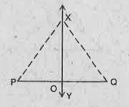
View Solution`Delta DEF` లో `bar DF` గరిష్ట భుజమైన , గరిష్ట కోణము విలువ
View Solution`Delta PQR` లో PQ > QR అయిన
View Solution`Delta ABC` విషయంలో కింది వాటిలో సరైనది ఏది?
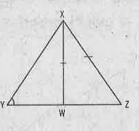
View Solution`Delta XYZ` లో YZ మద్య బిందువు 'W' మరియు XW=XZ గా అగుటకు నియమము
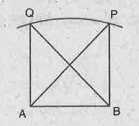
View Solutionపటంలో AB ఒక రేఖ ఖండము, PQ ఒక చపము అయిన
View Solutionపటంలో PA=PB మరియు QA=QB అయిన `/_POA` ఒక _____కోణము
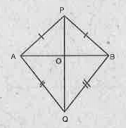
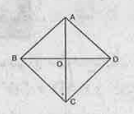
View Solutionరాంబస్ ABCD లో 'Delta AOB ~=`
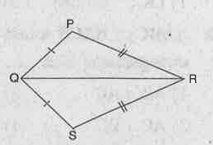
View Solutionపటంలో PQ=SQ, PR=SR అయిన `Delta PQR ~= Delta SQR` ____సర్వసమనము ద్వారా అగును.
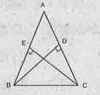
View Solution`Delta ABC` లో BD మరియు CE ఇన్నతులు సమానమైన `Delta DCB ~= Delta EBC` అగు నియమం
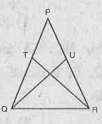
View Solution`Delta PQR` లో PQ=PR మరియు RT మరియు QU లు మధ్యగతలైన `Delta QRT ~= Delta RQU` అగు నియమం
View Solution`Delta ABC` లో AB=AC మరియు `AP _|_ BC` అయిన `/_B = /_C` అని నిరూపణకు ఉపయోగపడు నియమం
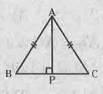
View Solutionకింది వాటిలో త్రిభుజ నిర్మాణానికి సరిపడని కొలతలు
View Solution4 సెంమీ మరియు 6 సెంమీ ల కొలతలతో త్రిభుజ నిర్మాణానికి అవసరమైన మరొక కొలతను గుర్తించుము
View Solutionకింది వాటిలో త్రిభుజాల సర్వసమననికి ఉపయోగపడు నియమం
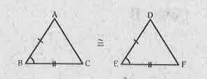
View Solutionకింది పటాల సర్వసమాన నిరూపణకు ఉపయోగపడు నియమం
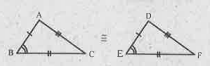
View Solutionకింది పటాలు ఎ నియమం ద్వారా తుల్యము?
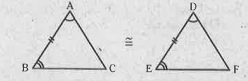
View Solutionకింది పటాలు ఎ నియమం ద్వారా తుల్యము?
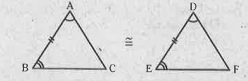
View Solution`Delta PQR` లో PQ = 5 సెంమీ, QR=12 సెంమీ మరియు PR = 13 సెంమీ అయిన `Delta PQR` ఒక ____త్రిభుజము
View Solutionఒకే ఆకారం మరియు పరిమాణము గల పటాలను ______పటలంటారు
View Solutionరెండు చతురస్రాలు సర్వసమానాలు అగుటకు వాటికి ఒకే _____ఉండాలి
View Solutionఏవైనా రెండు వృత్తాలు
View Solutionఒక త్రిభుజం యొక్క 3 కోణాలు మరొక త్రిభుజము యొక్క 3 కొనలకు సమానమైన అవి
View Solutionసమబాహు త్రిభుజము యొక్క కోణము
View Solution`Delta ABC` లో AB > AC అయిన
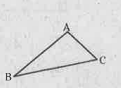
View Solutionదత్త పటాలను గణయనించగ ని పరిశీలన
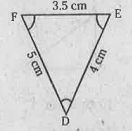
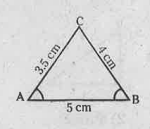 ,
,
View Solutionదత్త పటంలో AB మరియు CD లు 'O' వద్ద ఖండించుకున్న OA=OB, OD=OC అయినAD∥BC అనినిరూపించండి
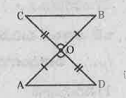
View Solutionపటంలో `Delta ABC ~= Delta CDA` అగుటకు నియమం

View Solution`Delta ABC` లో BD మరియు CE ఇన్నతులు సమానమైన `Delta DCB ~= Delta EBC` అగు నియమం

View Solutionసరైన ఎంపిక ద్వారా జతపరుచుము
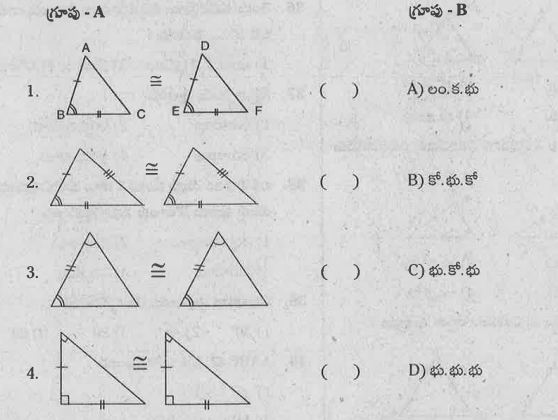
View Solutionసరైన ఎంపిక ద్వారా జతపరుచుము
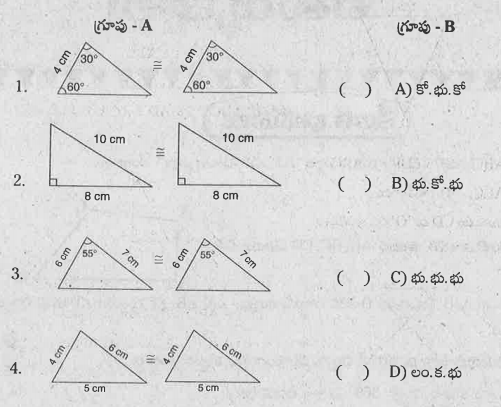
View Solution
Exercise questions and complete solutions for chapter త్రిభుజాలు of VGS MATHS (TELUGU) of Class 9