Level 3 from ARIHANT PHYSICS (HINGLISH) KINETIC THEORY OF GASES for Class 11
| Class 11 | PHYSICS |
| Chapter | KINETIC THEORY OF GASES |
| ARIHANT PHYSICS (HINGLISH) | Level 3 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
Find the number of atoms in molecule of a gas for which the ratio of specific heats at constant pressure and constant volumeλ becomes 2521 times if the rotational degree of freedom of its molecules are frozen. Assume that the gas molecules originally had translational and rotational degree of freedom. View SolutionQuestion 3
An ideal gas expands following a relation P2ρ= constant, where P = pressure and ρ = density of the gas. The gas is initially at temperature T and density ρ and finally its density becomes ρ3.
(a) Find the final temperature of the gas. (b) Draw the P – T graph for the process. View SolutionQuestion 4
A container having volume V contains N atoms of a gas X. 2 N atoms of another gas Y is injected into the container and temperature is raised to T and maintained constant. At this temperature the atoms of X and Y combine to form molecule X2 Y. Find the pressure inside the container after the reaction is completedView SolutionQuestion 6
A container of volume V1 has an ideal gas of molar mass M1 at pressure P1 and temperature T1. Another container of volume V2 has another ideal gas of molar mass M2 at pres- sure P2 and temperature T2. Two gases are mixed in a vessel and acquire an equilibrium temperature and pressure of T0 and P0 respectively. Find the density of the mixture. View SolutionQuestion 7
A U shaped tube has two arms of equal cross section and lengths l1=80 cm and l2=40 cm. The open ends are sealed with air in the tube at a pressure of 80 cm of mercury. Some mercury is now introduced in the tube through a stopcock connected at the bottom (the air is not allowed to leak out). In steady condition the length of mercury column in the shorter arm was found to be 10 cm. Find the length of the mercury column in the longer arm. Neglect the volume of the part of the tube connecting two arms and assume that the temperature is constant.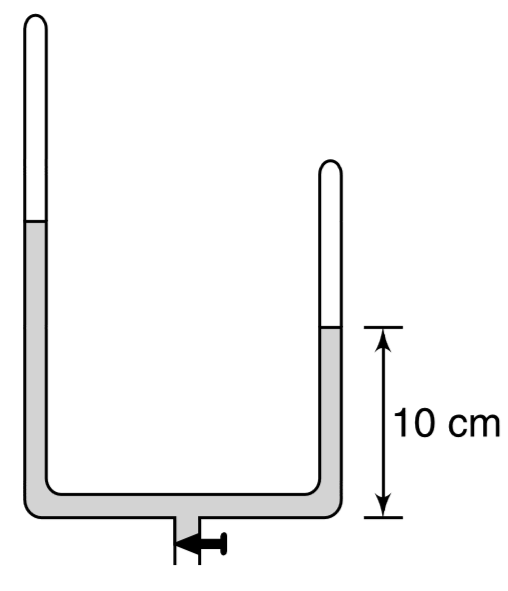 View Solution
View SolutionQuestion 8
Tidal volume is that volume of air which is inhaled (and exhaled) in one breath by a human during quiet breathing. For a normal man this volume is close to 0.6 litre. 35% of oxygen (in terms of molecular count) gets converted into carbon – di – oxide in the exhaled air. Nearly 21% of the air that we breath in is oxygen. Assume that a man is breathing when the air is at STP and the moisture content of inhaled and exhaled air is same. Estimate the difference in mass of an inhaled breath and exhaled breath. View SolutionQuestion 9
A cylindrical container of volume V0 is divided into two parts by a thin conducting separator of negligible mass. The walls of the container are adiabatic. Ideal gases are filled in the two parts such that the pressures are P0 and 2P0 when the separator is held in the middle of the container (see figure). Now the separator is slowly slid and released in a position where it stays in equilibrium. Find the volume of the two parts.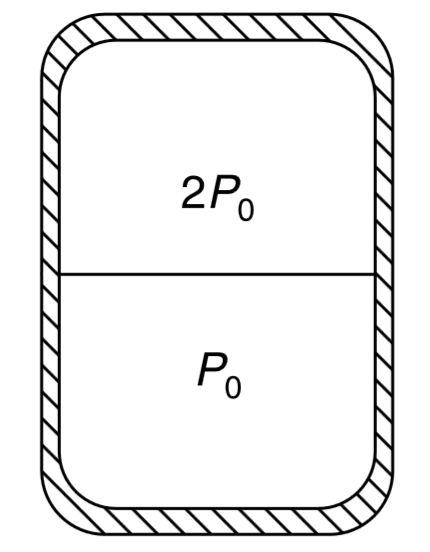 View Solution
View SolutionQuestion 10
Two identical glass bulbs are interconnected by a thin tube of negligible volume. An ideal gas is filled in the bulbs at STP. One bulb is placed in a tub of melting ice and the other bulb is placed in a hot bath. The gas pressure in the bulbs becomes 1.5 times. Find the tem perature of the hot bath. Which bulb has more gas?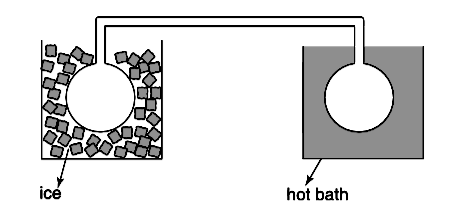 View Solution
View SolutionQuestion 12
A cylindrical tube of cross sectional area A and length L is filled with an ideal gas. Temperature of the gas varies linearly from T0 at one end to2T0 at the other end. Calculate the number of mole of the gas in the tube assuming pressure to be uniform throughout equal to P.View SolutionQuestion 14
A jar contains a gas and a few drops of water at absolute temperture T1. The pressure in the jar is 830mm of mercury. The temperature of the jar is reduced by 1%. The saturation vapour pressures of water at the two temperatures are 30mm of mercury and 25mm of mercury. Calculate the new pressure in the jar. View SolutionQuestion 15
A close container of volume 0.02m3 contains a mixture of neon and another gas A of unknown molecular mass. The container contains 4 g of Neon and 24 g of gas A. At a temperature of 27∘C the pressure of the mixture is 105N/m2. Is there any possibility of finding gas A in the atmosphere of a planet of radius 600 km and mean density r=5x×103kg/m3 ?
Temperature of the planet is 2200∘C.
Molar molecular mass of neon = 20 g,
Gas constant R=8.314J mol–1K–1
Gravitational constant G=6.67x×10–11Nm2kg–2 View SolutionQuestion 16
We know that volume (V ) occupied by a substance scales as x3 , where x is the average distance between its molecules. Assume that water vapour at 100∘C and atmospheric pressure has average intermolecular separation equal to xv and for liquid water at 100∘C the intermolecular separation is xw. Find the ratio Xvxw considering density of water at 100∘C to be 1.0x×103kg/m3 and taking water vapour as an ideal gas. Atmospheric pressure P0=1.0x×105N/m2 , Gas constant R=8.3J mol–1K–1. View SolutionQuestion 17
The diameter of molecules of a gas, considered as sphere, is about 3x×10–10 m. Assume the entire volume occupied by the gas to be divided into cubic cells with one molecule per cell. Estimate the distance between molecules in terms of molecular diameter under standard conditions. View SolutionQuestion 18
The core of the sun is a plasma. It is at a temperature of the order of 107 K and contains equal number of protons and electrons. The density of the core of the Sun is 105kgm–3 . Assume that molar mass of proton is 1g mol–1 and the mass of an electron to be negligible compared to the mass of a proton. Estimate the pressure at the core of the sun. Assume that plasma behaves like an ideal gas. View SolutionQuestion 20
A cylinder of oxygen, used as medical aid, has a volume of 16 L. It is filled to a pressure of 1.37x×107Nm–2 above the atmospheric pressure at room temperature of 300 K. When in use, the flow rate at atmospheric pressure is 2.4L/min. How long will the cylinder last? Atmospheric pressure is 105Nm–2. View SolutionQuestion 21
It is known that pressure of a gas increases if–
(A) You increase the temperature of the gas while holding its volume constant.
(B) You compress the gas holding its temperature constant.
(i) In which of the two cases [A or B] the average impulse imparted by a gas molecule to the container wall during a collision increases?
(ii) In which of the two cases the frequency of collisions of gas molecules with the container wall increases. View SolutionQuestion 23
An insulated cylindrical vessel is divided into three identical parts by two partitions 1 and 2. The left part contains O2 gas, the middle part has N2 and the third chamber has vacuum. The average molecular speed in oxygen chamber is V0 and that in nitrogen chamber is √87V0. Pressure of the gases in two chambers is same. Partition 1 is removed and the gases are allowed to mix. Now the stopper holding the partition 2 is removed and it slides to the right wall of the container, so that the mixture of gases occupy the entire volume of the container.
Find the average speed of O2 molecules now.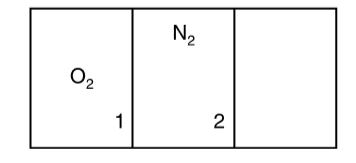 View Solution
View SolutionQuestion 24
In a cylindrical container two pistons enclose gas in two compartments as shown in the figure. The pistons have negligible thickness and can move without friction. The sys- tem is originally in equilibrium. The outer piston is slowly moved out by 10 cm and the inner piston is found to move by 4 cm. Find the distance of the inner piston in equilibrium from the closed end of the cylinder if the outer piston is slowly moved out of the cylinder. Assume temperature of the gas to remain constant.
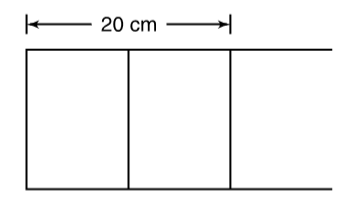 View Solution
View SolutionQuestion 28
A cylindrical container of length 2 L is rotating with an angular speed w about an axis passing through its centre and perpendicular to its length. Its contains an ideal gas of molar mass M. Calculate the ratio of gas pressure at the end of the container to the pressure at its centre. Neglect gravity and assume that temperature of the gas throughout the container is T.
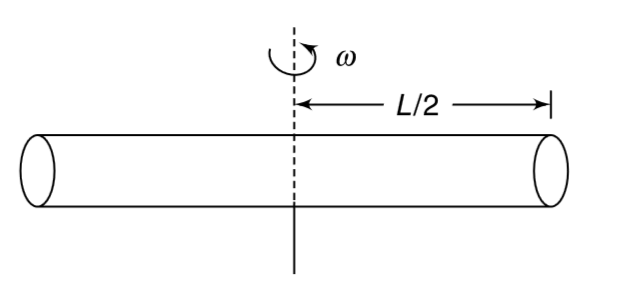 View Solution
View SolutionQuestion 29
A container of volume V = 16.6 litre contains a mixture of hydrogen and helium at a temperature of 300 K. The pressure in the container is 6x×105 Pa and mass of the mixture is 10 g. Let f1 and f2 be the number of collisions made by the hydrogen and helium molecules with unit area of the container wall in unit time. Calculate the ratio f1f2.
[R=8.3J mol–1K–1].View SolutionQuestion 30
An ideal gas is enclosed in a cylinder having cross sectional area A. The piston of mass M has its lower face inclined at θ to the horizontal. The lower face of the piston also has a hemispherical bulge of radius r. The atmospheric pressure is P0.
(a) Find pressure of the gas.
(b) The piston is slowly pulled up by a distance x. During the process the piston is always maintained in equilibrium by adding heat to the gas. [It means if the piston is left at any stage it will stay there in equilibrium]. Find change in temperature of the gas. Number of mole of the gas in the cylinder is one.
 View Solution
View SolutionQuestion 31
A beam of gas molecules is incident normally on a plate AB. Each gas molecule has mass m and velocity V. The incident beam falls on an area A on the plate and all the molecule strike the plate elastically. Number of molecules in unit volume of the beam is n. When the plate is moved to right (see fig.) a force F1 is needed to keep it moving with constant velocity u (>V) . When the plate is moved to left with constant velocity u, an external force F2 is needed. Find F2–F1.
 View Solution
View SolutionQuestion 32
Atmosphere of a planet contains only an ideal gas of molar mass M0. The temperature of the atmosphere varies with height such that the density of atmosphere remains same throughout. The planet is a uniform sphere of mass M and radius ‘a’. Thickness of atmosphere is small compared to ‘a’ so that acceleration due to gravity can be assumed to be uniform throughout the atmosphere.
(a) Find the temperature difference between the surface of the planet and a point at height H in its atmosphere
(b) If the rms speed of gas molecules near the surface of the planet is half the escape speed, calculate the temperature of the atmosphere at a height H above the surface. Assume CpCV=γ for the atmospheric gasView SolutionQuestion 33
The Maxwell-Boltzmann distribution of molecular speeds in a sample of an ideal gas can be expressed as
f=4√π(m2kT)3/2v2e−mv22kT.dv
Where f represent the fraction of total molecules that have speeds between v and v + dv.m, k and T are mass of each molecule, Boltzmann constant and temperature of the gas.
(a) What will be value of ∫v=∞v=0fdv?
(b) It is given that ∫∞0v3e−av2dv=12a2
Find the average speed of gas molecules at temperature T. View SolutionQuestion 34
A large cylindrical tower is kept vertical with its ends closed. An ideal gas having molar mass M fills the tower. Assume that temperature is constant throughout, acceleration due to gravity (g) is constant throughout and the pressure at the top of the tower is zero.
(a) Calculate the fraction of total weight of the gas inside the tower that lies above certain height h.
(b) At what height h0 the quantity of gas above and below is same. How does the value of h0 change with temperature of the gas in the tower? View SolutionQuestion 35
A physics book was found on a newly discovered island in 18th century. A problem in the book was as follows. “1 pinch of an ideal gas is kept in a container of volume 1.5 volka. When the temperature is 40 tapu, the gas pressure is 25 phatka. When the temperatue is reduced to – 20 tapu the gas pressure becomes 10 phatka. Find the temperature of absolute zero in tapu. View SolutionQuestion 36
A L shaped container has dimensions shown in the fig. It has circular cross section of radius R. It is placed on a smooth horizontal table. The container is divided into two equal sections by a membrane AB. One section contains nitrogen and the other one contains oxygen. Temperature of both sides is same but pressure in the compartment having N2 is 4 times that in the other compartment. Due to some reason the membrane gets punctured. Find the distance moved by the cylinder if the cylinder is constrained to move in x direction only [with the help of guiding walls W1 and W2]. There is no friction anywhere and mass of the cylinder and membrane is negligible
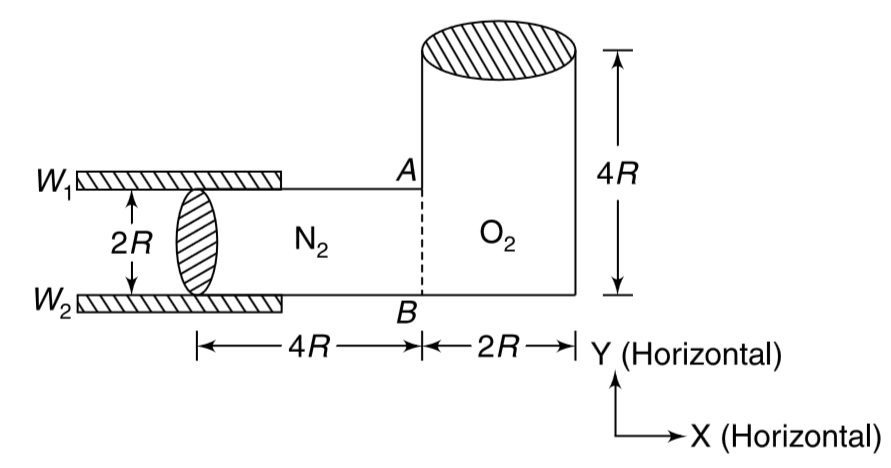 View Solution
View SolutionQuestion 37
(a) Assume the atmosphere as an ideal gas in static equilibrium at constant temperature T0. The pressure on the ground surface is P0. The molar mass of the atmosphere is M. Calculate the atmospheric pressure at height h above the ground.
(b) To be more realistic, let as assume that the temperature in the troposphere (lower part of the atmosphere) decreases with height as shown in the figure. Now calculate the atmospheric pressure at a height h0 above the ground.
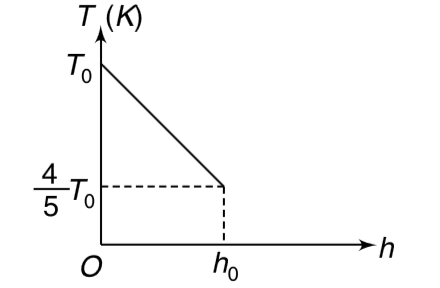 View Solution
View SolutionQuestion 38
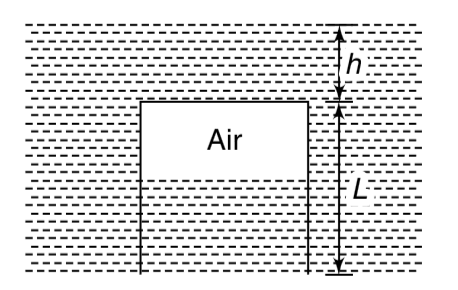
A cylindrical container has cross sectional area of A=0.05m2 and length L = 0.775 m. Thickness of the wall of the container as well as mass of the container is negligible. The container is pushed into a water tank with its open end down. It is held in a position where its closed end is h = 5.0 m below the water surface. What force is required to hold the container in this position? Assume temperature of air to remain constant.
Atmospheric pressure P0=1x×105 Pa, Acceleration due to gravity g=10m/s2
Density of water = 103kg/m3
 View Solution
View SolutionQuestion 39
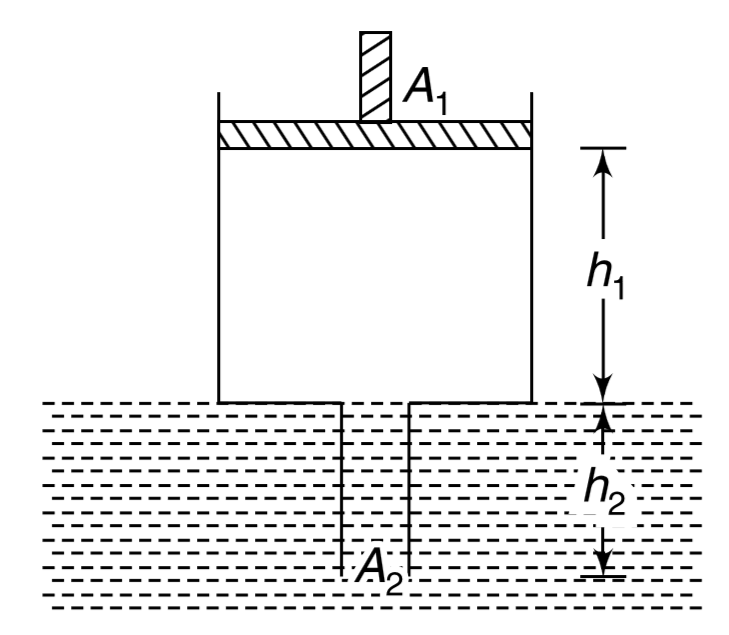
A syringe has two cylindrical parts of cross sectional area A1=4cm2 and A2=1cm2. A mass less piston can slide on the inner wall of the part having cross section A1. The end of the part having cross section A2 is open. Syringe is dipped in a large water tank such that the narrower part remains completely submerged and the wider part is filled with air. The length shown in figure are h1=55cm and h2=100 cm. The piston is pushed down by a distance x such that 25% of the air inside the syringe is expelled out through the open end of the narrower part. Assume that the temperature of air remains constant and calculate x.
Density of water = 103kgm–3,g=10ms–2, Atmospheric pressure = 105Nm–2.
 View Solution
View SolutionQuestion 42
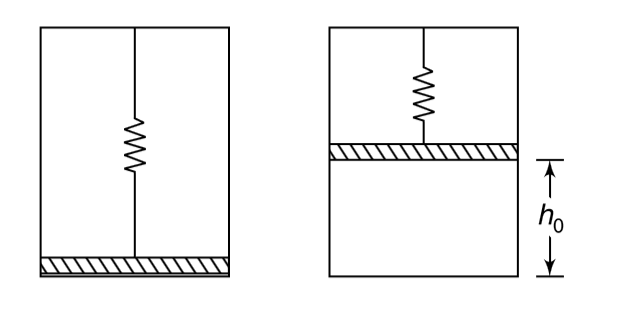
A freely sliding massive piston is supported by a spring inside a vertical cylinder as shown. When all air is pumped out of the container, the piston remains in equilibrium with only a tiny gap between the piston and the bottom surface of the cylinder. An ideal gas at temperature T0 is slowly injected under the piston so that it rises to height h0 (see figure). Calculate the height of the piston from the bottom of the container if the temperature of the gas is slowly raised to 4T0.
 View Solution
View SolutionQuestion 43
An ideal gas is inside a cylinder with a piston that can move freely. The walls of the cylinder and piston are non- conducting. The piston is being moved out of the cyl- inder at a constant speed u.
(a) Consider a gas molecule of mass m moving with speed v(>>u). It hits the piston elastically at an angle of incidence q. Calculate the loss in kinetic energy of the molecule.
(b) If the area of piston is A and pressure of the gas is P, calculate the rate of decreases of molecular kinetic energy of the gas sample.
(c) Ifu>> molecular velocities, at what rate will the gas lose its molecular kinetic energy
 View Solution
View SolutionQuestion 44
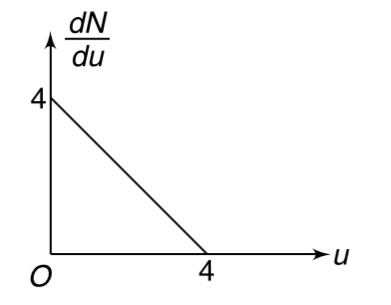
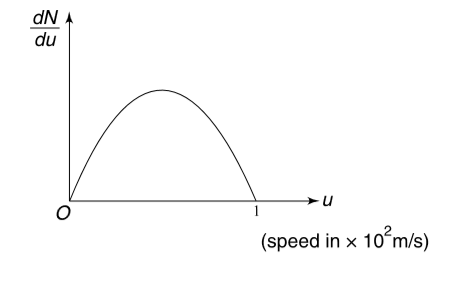
The speed distribution of molecules in a sample of a gas is shown in the figure. The graph between dNdu and u is a parabola and total number of molecules in the sample is N0.
(a) Calculate the rms speed of the molecules.
(b) Calculate the total translational kinetic energy of molecules if mass of the sample is 10 g.
 View Solution
View SolutionQuestion 45
A cylindrical container is divided into three parts by two tight fitting pistons. The pistons are connected by a spring. The region between the pistons is vacuum and the other two parts have same number of moles of an ideal gas. Initially, both the gas chambers are at temperature T0 and the spring is compressed by 1 m. Length of both gas chambers is 1 m in this position. Now the temperature of the left and right chambers are raised to 4T03 and 5T03 respectively. Find the final compression in the spring in equilibrium. Assume that the pistons slide without friction
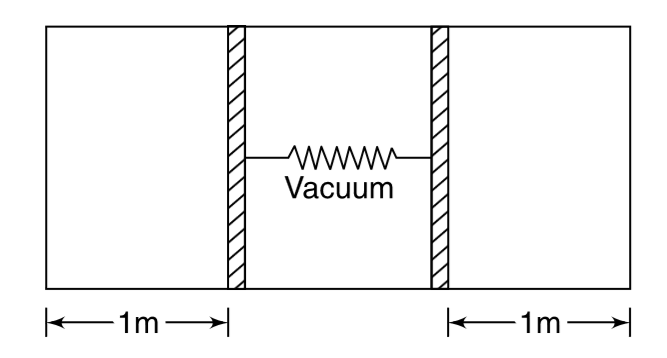 View Solution
View SolutionQuestion 46
A helium balloon has its rubber envelope of weight wRubber and its is used to lift a weight of wLoad. The volume of fully inflated balloon is V0. The atmospheric temperature is T0 throughout and the atmospheric pressure is known to change with height y according to equation P=P0e–ky where k is a positive constant and P0 is atmospheric pres- sure at ground level. The balloon is inflated with sufficient amount of helium so that the net upward force on is F0 at the ground level. Assume that pressure inside the balloon is always equal to the outside atmospheric pressure. Density of air and helium at ground level is ρa and ρHe respectively.
(a) Find the number of moles (n) of the helium in the balloon.
For following two questions assume n to be a known quantity.
(b) Find the height (y(0)) at which the balloon is fully inflated.
(c) Prove that the balloon will be able to rise to height y0 if nRT0gP0(ρa−ρHg)>wRubber+wLoadView Solution