All Questions from ARIHANT PHYSICS (HINGLISH) TEMPERATURE AND THERMAL EXPANSION for Class 11
| Class 11 | PHYSICS |
| Chapter | TEMPERATURE AND THERMAL EXPANSION |
| ARIHANT PHYSICS (HINGLISH) | All Questions |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
In a temperature scale X ice point of water is assigned a value of 20∘ X and the boiling point of water is assigned a value of 220∘ X . In another scale Y the ice point of water is assigned a value of −20∘ Y and the boiling point is given a value of 380∘ Y. At what temperature the numerical value of temperature on both the scales will be same? View SolutionQuestion 2
The length of the mercury column in a mercury-in- glass thermometer is 5.0 cm at triple point of water. The length is 6.84 cm at the steam point. If length of the mercury column can be read with a precision of 0.01 cm, can this thermometer be used to distinguish between the ice point and the triple point of water? View SolutionQuestion 3
What effect the following changes will makes to the range, sensitivity and responsiveness of a mercury in glass thermometer – (a) Increase in size of the bulb. (b) Increase in diameter of the capillary bore. (c) Increase in length of the stem. (d) Use of thicker glass for the bulb. View SolutionQuestion 6
A pendulum based clock keeps correct time in an aeroplane flying uniformly at a height h above the surface of the earth. The cabin temperature inside the plane is 10∘C. The same pendulum keeps correct time on the surface of the earth when temperature is 30∘C. Find the coefficient of linear expansions of the material of the pendulum. You can assume that h ltlt R (radius of the earth) View SolutionQuestion 7
A liquid having coefficient of volume expansion γ0 is filled in a cylindrical glass vessel. Glass has a coefficient of linear expansion of αg. The liquid along with the container is heated to raise their temperature by ΔT. Mass of the container is negligible. (a) find relationship between αg and γ0 if it was found that the centre of mass of the system did not move due to heating.
(b) Find relationship between αg and γ0 if the fraction of volume of the container occupeid by the liquid does not change due to heating. View SolutionQuestion 8
A water in glass thermometer has density of water marked on its stem [Density of water is the thermometric property in this case]. When this thermometer is dipped in liquid A the density of water read is 0.99995 g cm3. Thereafter it is dipped in liquid B and the reading remains unchanged. Maximum density of water is 1.00000 g cm−3. (a) Can we say that liquid A and B are necessarily in thermal equilibrium? (b) If two liquids are mixed and the thermometer is inserted in the mixture, the height of water column in stem is found to change (i.e. reading is different from 0.99995 g cm−3). Has the height increased or decreased? View SolutionQuestion 10
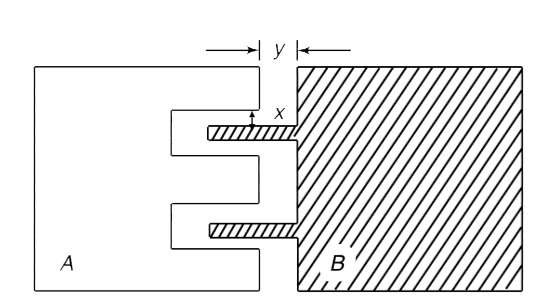
Containers A and B contain a liquid up to same height. They are connected by a tube (see figure). (a) If the liquid in container A is heated, in which direction will the liquid flow through the tube. (b) If the liquid in the container B is heated in which direction will the liquid flow through the tube? Assume that the containers do not expand on heating.
 View Solution
View SolutionQuestion 11
Height of mercury in a barometer is h0=76.0 cm at a temperature of θ1=20∘C. If the actual atmospheric pressure does not change, but the temperature of the air, and hence the temperature of the mercury and the tube rises to θ2=35∘C, what will be the height of mercury column in the barometer now? Coefficient of volume expansion of mercury and coefficient of linear expansion of glass are
γHg=1.8×10−4.∘C−1,αg=0.09×10−4.∘C−1View SolutionQuestion 13
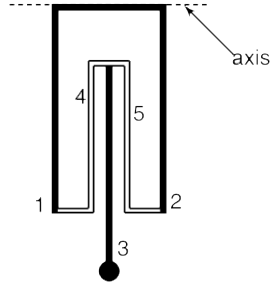
Pendulum of a clock consists of very thin sticks of iron and an alloy. At room temperature the iron sticks 1 and 2 have length L0 each. Length of each of the two alloy sticks 4 and 5 is 0 and the length of iron stick 3 (measured up to the centre of the iron bob) is l0. Thickness of connecting strips are negligible and mass of everything except the bob is negligible. The pendulum oscillates about the horizontal axis shown in the figure. It is desired that the time period of the pendulum should not change even if temperature of the room changes. Find the coefficient of linear expansion (α) of the alloy if the coefficient of linear expansion for iron is α0.
 View Solution
View SolutionQuestion 14
Two samples of a liquid have volumes 400 cc and 220 cc and their temperature are 10∘C and 110∘C respectively. Find the final temperature and volume of the mixture if the two samples are mixed. Assume no heat exchange with the surroundings. Coefficient of volume expansion of the liquid is g=10−3.∘C−1 and its specific heat capacity is a constant for the entire range of temperature.View SolutionQuestion 15
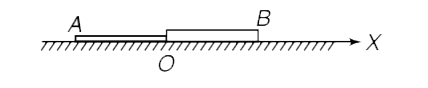
A composite bar has two segments of equal length L each. Both segments are made of same material but cross sectional area of segment OB is twice that of OA. The bar is kept on a smooth table with the joint at the origin of the co - ordinate system attached to the table. Temperature of the composite bar is uniformly raised by Δθ. Calculate the x co-ordinate of the joint if coefficient of linear thermal expansion for the material is α∘C−1
 View Solution
View SolutionQuestion 16
Two rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length l1, coefficient of linear expansion α1 and Young's modulus Y1. The correcsponding quantities for second rod are l2,α2 and Y2. The temperature of both the rods is now raised by t∘C.
i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities.
ii. Also find the length of the rods at higher temperature.
 View Solution
View SolutionQuestion 17
Two rods of equal cross-sections, one of copper and the other of steel are joined to from a composite rod of length 2.0m at 20∘C the length of the copper rod is 0.5m. When the temperature is raised to 120∘C, the length of composite rod increases to 2.002m. If the composite rod is fixed between two rigid walls and thus not allowed to expand, it is found that the length of the component rod also do not change with increase in temperature. Calculate the Young's modulus of steel. Given Young's modulus of copper =1.3×1011N/m2 the coefficient of linear expansion of copper αC=1.6×10−5/.∘cView SolutionQuestion 18
A beaker contains a liquid of volume V0. A solid block of volume V floats in the liquid with 90% of its volume submerged in the liquid. The whole system is heated to raise its temperature by Δθ. It is observed that the height of liquid in the beaker does not change and the solid in now floating with its entire volume submerged. Calculate Δθ. It is given that coefficient of volume expansion of the solid and the glass (beaker) are γs and γg respectively.
 View Solution
View SolutionQuestion 19
Assume that the coefficient of linear expansion of the material of a rod remains constant, equal to α∘C−1 for a fairly large range of temperature. Length of the rod is L0 at temperature θ0. (a) Find the length of the rod at a high temperature θ. (b) Approximate the answer obtained in (a) to show that the length of the rod for small changes in temperature is given by L=L0[1+α(δ−δ0)] View SolutionQuestion 20
In a compensated pendulum a triangular frame ABC is made using two different metals. AB of length l1 is made using a metal having coefficient of linear expansion α1. BC and AC of length l2 each have coefficient of linear expansion α2. A heavy bob is attached at C. Pendulum can oscillate about the pivot D. Find l2l1 so that distance of bob from the pivot point D does not change with change in temperature.
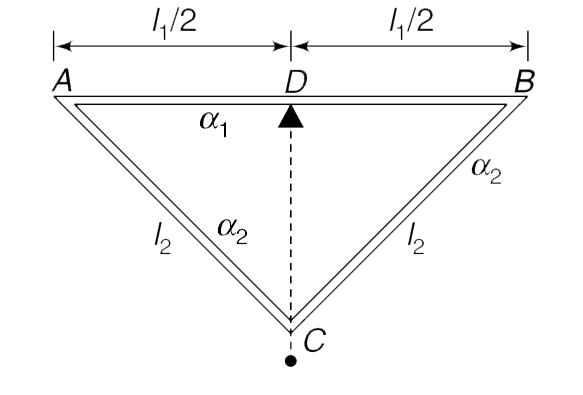 View Solution
View SolutionQuestion 21
A thin uniform rod of mass M and length l is rotating about a frictionless axis passing through one of its ends and perpendicular to the rod. The rod is heated uniformly to increases its temperature by Δθ. Calculate the percentage change in rotational kinetic energy of the rod. Explain why the answer is not zero. Take coefficient of linear expansion of the material of the rod to be α.View SolutionQuestion 22
(a) A steel tank has internal volume V0 (= 100 litre). It contains half water ( volume = V02 ) and half kerosene oil at temperature θ1=10∘C
Calculate the mass of kerosene that flows out of the tank at temperature of θ2=40∘C. Coefficient of cubical expansion for different substances are: γk=10−3.∘C−1,γw=2×10−4.∘C−1,γsteel=1.2×10−5.∘C−1. density of kerosene at 10∘C is ρ1=0.8kg /litre.
(b) In the last problem the height of water in the container at θ1=10∘C is H1=1.0m. Find the height of water at θ2=40∘C.
 View Solution
View SolutionQuestion 23
A metal cylinder of radius R is placed on a wooden plank BD. The plank is kept horizontal suspended with the help of two identical string AB and CD each of length L. The temperature coefficient of linear expansion of the cylinder and the strings are a1 and a2 respectively. Angle q shown in the figure is 30∘. It was found that with change in temperature the centre of the cylinder did not move. Find the ratio α1α2 , if it is know that L = 4R. Assume that change in value of θ is negligible for small temperature changes
 View Solution
View SolutionQuestion 24
A vernier calliper has 10 divisions on vernier scale coinciding with 9 main scale divisions. It is made of a material whose coefficient of linear expansion is α=10−3.∘C−1. At 0∘C each main scale division = 1mm. An object has a length of 10 cm at a temperature of 0∘C and its material has coefficient of linear expansion equal to α1=1×10−4.∘C−1. The length of this object is measured using the said vernier calliper when room temperature is 50∘C. (a) Find the reading on the main scale and the vernier scale (b) The same object is measured (at 50∘C) using a wooden scale whose least count is 1mm. Write the measured reading using this scale assuming it to be correct at all temperature. View SolutionQuestion 25
A rectangular tank contains water to a height h. A metal rod is hinged to the bottom of the tank so that it can rotate freely in the vertical plane. The length of the rod is L and it remains at rest with a part of it lying above the water surface. In this position the rod makes an angle θ with the vertical. Assume thaty=cosθ and find fractional change in value of y when temperature of the system increases by a small value ΔT.Coefficient of linear expansion of material of rod and the tank areα1 and α2 respectively. Coefficient of volume expansion of water is λ. What is necessary condition for θ to increase?
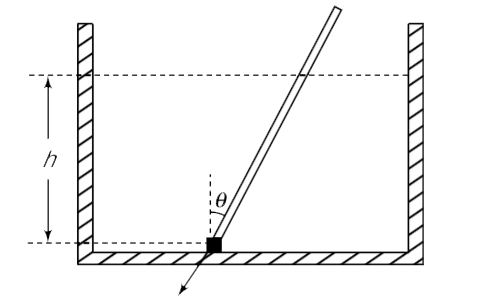 View Solution
View SolutionQuestion 27
In design of a compensated pendulum, a light metal rod of length L0 = 1.0 m is attached to a glass tube filled with mercury. Neglecting the mass of the glass tube as well, calculate the height of mercury column in the glass tube so that centre of mass of this system does not rise or fall with temperature Given : λ)Hg)=1.82×10−4K−1,αglass')=9xx10^(-6),alpha_(mηl=1.2×10−5K−1
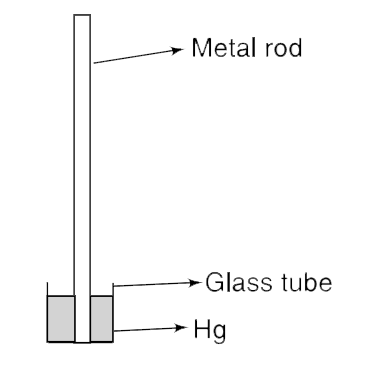 View Solution
View Solution