Level 3 from ARIHANT PHYSICS Chapter 8 KINEMATICS for Class 11
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| ARIHANT PHYSICS | Level 3 |
| Medium | English |
| Academic Year | 2023-2024 |
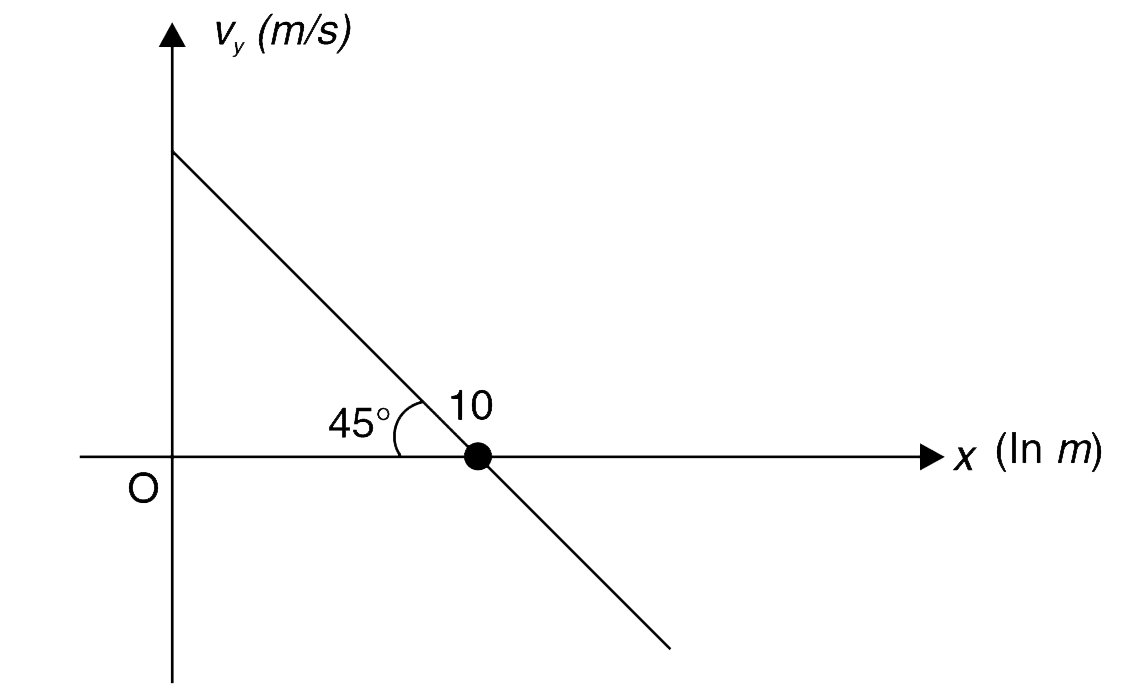
Question 1
A car manufacturer usually tells a optimum speed (V0) at which the car should be driven to get maximum mileage. In order to find the optimum speed for a new model, an engineer of the car company experimented a lot and finally plotted a graph between the extreme time t (defined as number of hours a tank full of petrol lasts) vs the constant speed V at which car was run.
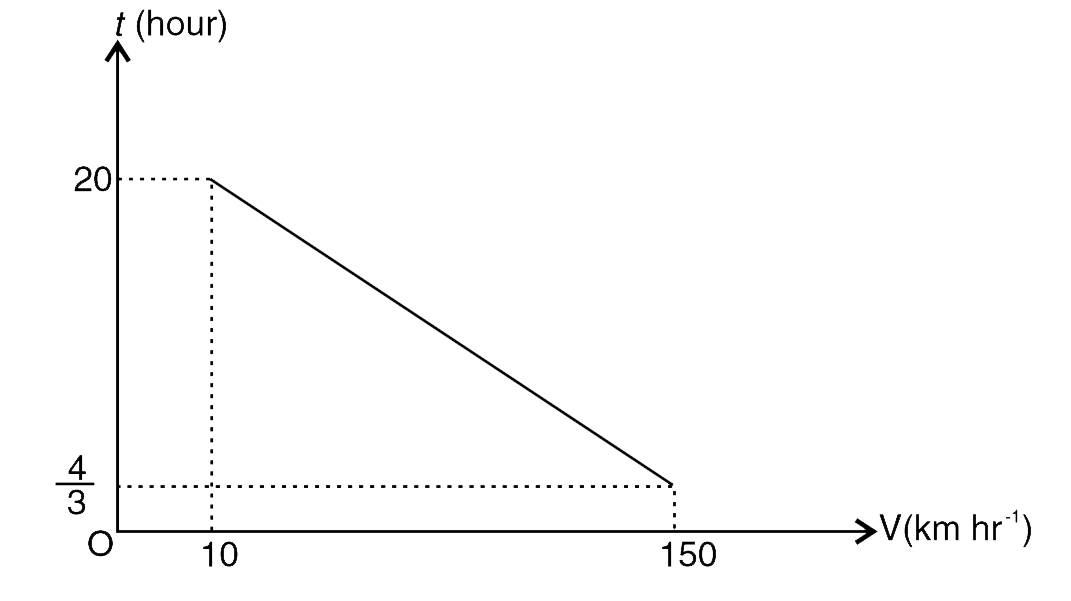
(a) Calculate the optimum speed V0 for this new model.
(b) If the fuel tank capacity of this car is 50 litre, what maximum mileage can be obtained from this car?View SolutionQuestion 2
While starting from a station, a train driver was instructed to stop his train after time T and to cover maximum possible distance in that time.
(a) If the maximum acceleration and retardation for the train are both equal to ‘a’, find the maximum distance it can cover.
(b) Will the train travel more distance if maximum acceleration is ‘a’ but the maximum retardation caused by the brakes is ‘2a’? Find this distance. View SolutionQuestion 3
Two particles 1 and 2 start simultaneously from origin and move along the positive X direction. Initial velocity of both particles is zero. The acceleration of the two particles depends on their displacement (x) as shown in fig.
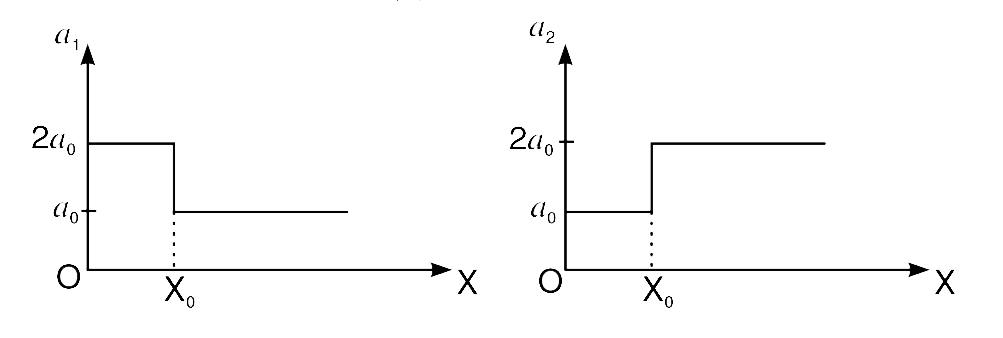
(a) Particles 1 and 2 take t1 and t2 time respectively for their displacement to become x0. Find t2t1.
(b) Which particle will cover 2x0 distance in least time? Which particle will cross the point x=2x0 with greater speed?
(c) The two particles have same speed at a certain time after the start. Calculate this common speed in terms of a0 and x0.View SolutionQuestion 4
A cat is following a rat. The rat is running with a constant velocity u. The cat moves with constant speed v with her velocity always directed towards the rat. Consider time to be t=0 at an instant when both are moving perpendicular to each other and separation between them is L. View SolutionQuestion 5
(a) Prove that bodies starting at the same time t=0 from the same point, and following frictionless slopes in different directions in the same vertical plane, all lie in a circle at any subsequent time.
(b) Using the above result do the following problem. A point P lies above an inclined plane of inclination angle α. P is joined to the plane at number of points by smooth wires, running in all possible directions. Small bodies (in shape of beads) are released from P along all the wires simultaneously. Which body will take least time to reach the plane.
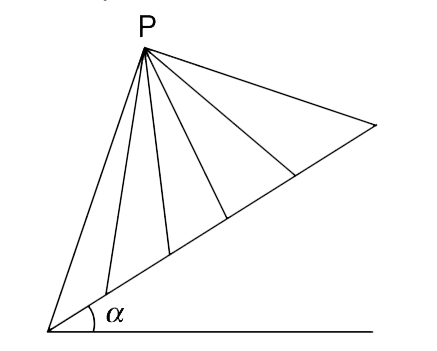 View Solution
View SolutionQuestion 6
The acceleration due to gravity near the surface of the earth is →g . A ball is projected with velocity →u from the ground.
(a) Express the time of flight of the ball.
(b) Write the expression of average velocity of the ball for its entire duration of flight. Express both answers in terms of →u and →g. View SolutionQuestion 7
A ball is projected from point O on the ground. It hits a smooth vertical wall AB at a height h and rebounds elastically. The ball finally lands at a point C on the ground. During the course of motion, the maximum height attained by the ball is H.
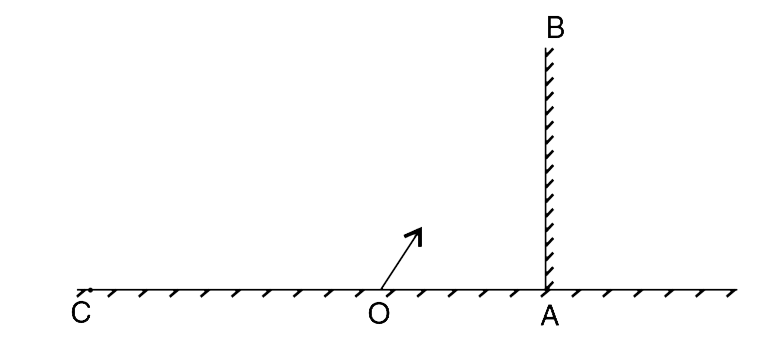
(a) Find the ratio hH if OAOC=13
(b) Find the magnitude of average acceleration of the projectile for its entire course of flight if it was projected at an angle of 45∘ to the horizontal. View SolutionQuestion 8
A boy can throw a ball up to a speed of u=30m/s . He throws the ball many a times, ensuring that maximum height attained by the ball in each throw is h=20m. Calculate the maximum horizontal distance at which a ball might have landed from the point of projection. Neglect the height of the boy. [g=10m/s2]View SolutionQuestion 9
A valley has two walls inclined at 37° and 53° to the horizontal. A particle is projected from point P with a velocity of u=20m/s along a direction perpendicular to the incline wall OA. The Particle hits the incline surface RB perpendicularly at Q. Take g=10m/s2 and find:
(a) The time of flight of the particle.
(b) Vertical height h of the point P from horizontal surface OR.
[tan37∘=34]
 View Solution
View SolutionQuestion 10

A ball is released in air above an incline plane inclined at an angle α to the horizontal. After falling vertically through a distance h it hits the incline and rebounds. The ball flies in air and then again makes an impact with the incline. This way the ball rebounds multiple times. Assume that collisions are elastic, i.e., the ball rebound without any loss in speed and in accordance to the law of reflection.
(a) Distance between the points on the incline where the ball makes first and second impact is l1 and distance between points where the ball makes second and third impact is l2. Which is large l1 or l2?
(b) Calculate the distance between the points on the incline where the ball makes second and fifth impact. View SolutionQuestion 11
A terrorist ‘A’ is walking at a constant speed of 7.5km/hr due West. At time t=0, he was exactly South of an army camp at a distance of 1 km. At this instant a large number of army men scattered in every possible direction from their camp in search of the terrorist. Each army person walked in a straight line at a constant speed of 6km/hr.
(a) What will be the closest distance of an army person from the terrorist in this search operation?
(b) At what time will the terrorist get nearest to an army person? View SolutionQuestion 12
A large wedge BCD, having its inclined surface at an angle θ=45∘ to the horizontal, is travelling horizontally leftwards with uniform velocity u=10m/s
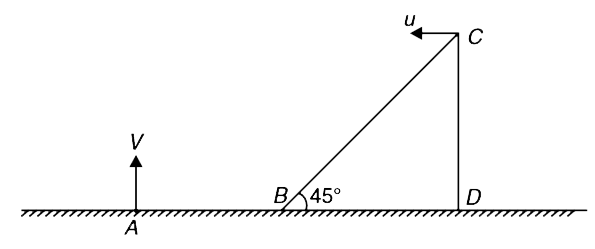
At some instant a particle is projected vertically up with speed V=20m/s from point A on ground lying at some distance right to the lower edge B of the wedge. The particle strikes the incline BC normally, while it was falling. [g=10m/s2]
(a) Find the distance AB at the instant the particle was projected from A.
(b) Find the distance of lower edge B of the wedge from point A at the instant the particle strikes the incline.
(c) Trace the path of the particle in the reference frame attached to the wedge. View SolutionQuestion 13
The speed of river current close to banks is nearly zero. The current speed increases linearly from the banks to become maximum (=V0) in the middle of the river. A boat has speed ‘u’ in still water. It starts from one bank and crosses the river. Its velocity relative to water is always kept perpendicular to the current. Find the distance through which the boat will get carried away by the current (along the direction of flow) while it crosses the river. Width of the river is l. View SolutionQuestion 14
A water sprinkler is positioned at O on horizontal ground. It issues water drops in every possible direction with fixed speed u. This way the sprinkler is able to completely wet a circular area of the ground (see fig). A horizontal wind starts blowing at a speed of u2√2.Mark the area on the ground that the sprinkler will now be able to wet.
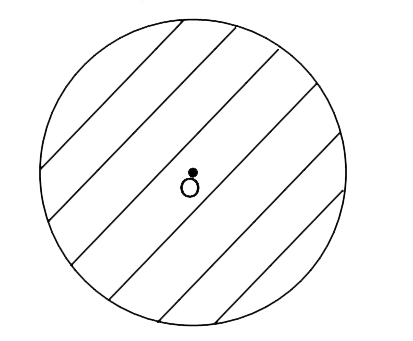 View Solution
View SolutionQuestion 15
A cylinder of radius R has been placed in a corner as shown in the fig. A wedge is pressed against the cylinder such that its inclined surfaces touches the cylinder at a height of 2R5 from thw ground. Now the wedge is pushed to the left at a constant speed V=15m/s. With what speed will the cylinder move?
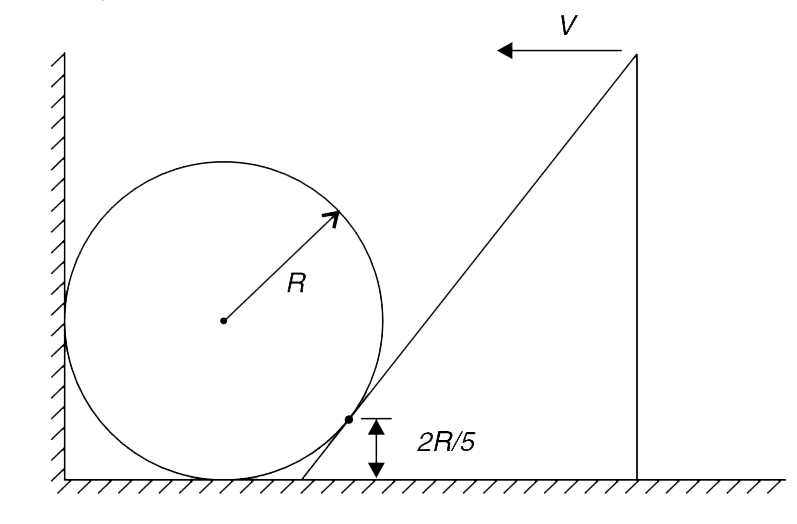 View Solution
View SolutionQuestion 16
The entrance to a harbour consists of 50m gap between two points A and B such that B is due east of A. Outside the harbour there is a 8km/hr current flowing due east. A motor boat is located 300 m due south of A. Neglect size of the boat for answering following questions-
(a) Calculate the least speed (Vmin) that the motor boat must maintain to enter the harbour.
(b) Show that the course it must steer when moving at Vmin does not depend on the speed of the current. View SolutionQuestion 17
Two small pegs (A and B) are at horizontal and vertical separation b and h respectively. A small block of mass M is suspended with the help of two light strings passing over A and B as shown in fig. The two string are always kept at right angles (i.e., <APB=90∘). Find the minimum possible gravitation potential energy of the mass assuming the reference level at location of peg A. [Hint: the potential energy is minimum when the block is at its lowest position]
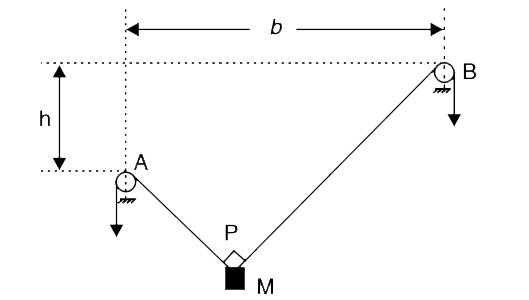 View Solution
View SolutionQuestion 18
A ball of mass m is projected from ground making an angle q to the horizontal. There is a horizontal wind blowing in the direction of motion of the ball. Due to wind the ball experiences a constant horizontal force of mg√3 in direction of its motion. Find θ for which the horizontal range of the ball will be maximum. View SolutionQuestion 20
In the arrangement shown in the figure, the block C begins to move down at a constant speed of 7.5cm/s at time t=0. At the same instant block A is made to start moving down at constant acceleration. It starts at M and its speed is 30cm/s when it reaches N(MN=20cm). Assuming that B started from rest, find its position, velocity and acceleration when block A reaches N.
 View Solution
View SolutionQuestion 21
A rocket prototype is fired from ground at time t=0 and it goes straight up. Take the launch point as origin and vertically upward direction as positive x direction. The acceleration of the rocket is given by
a=g2−kt2,0<t≤t0
=−g,t>t0
Where t0=√3g2k
(a) Find maximum velocity of the rocket during the up journey.
(b) Find maximum height attained by the rocket.
(c) Find total time of flight.View SolutionQuestion 22
A man standing inside a room of length L rolls a ball along the floor at time t=0. The ball travels at constant speed v relative to the floor, hits the front wall (B) and rebounds back with same speed v. The man catches the ball back at the wall A at time t0. The ball travelled along a straight line relative to the man inside the room. Another observer standing outside the room found that the entire room was travelling horizontally at constant velocity v in a direction parallel to the two walls A and B.

(a) Find the average speed of the ball in the time interval t=0 to t=t0 as observed by the observer outside the room.
(b) If the room has acceleration in the direction of its velocity draw a sketch of the path of the ball as observed by the observer standing outside. Assume that velocity of room was v at the instant the ball was released. View SolutionQuestion 23
There is a tall cylindrical building standing in a field. Radius of the cylinder is R=8m. A boy standing at A (at a distance of 10 m from the centre of the cylindrical base of the building) knows that his friend is standing at B behind the building. The line joining A and B passes through the centre of the base of the building. Distance between A and B is 50 m. A wants to throw a ball to B but he realizes that the building is too tall and he cannot throw the ball over it. He throws the ball at a speed of 20m/s such that his friend at B has to move minimum distance to catch it.

(a) What is the minimum distance that boy at B will have to move to catch the ball?
(b) At what angle to the horizontal does the boy at A throws the ball? Assume that the ball is released and caught at same height above the ground.
[Take g=10m/s2 and sin−1(0.75)≅48.6∘View SolutionQuestion 24
A wet umbrella is held upright (see figure). The man holding it is rotating it about its vertical shaft at an angular speed of ω=5 rad s–1. The rim of the umbrella has a radius of r=0.5 m and it is at a height of H=1.8 m from the floor. The man holding the umbrella gradually increases the angular speed to make it 2ω. Calculate the area of the floor that will get wet due to water drops spun off the rim and hitting the floor. [g=10m/s2].
 View Solution
View SolutionQuestion 25
A ball is projected vertically up from ground. Boy A standing at the window of first floor of a nearby building observes that the time interval between the ball crossing him while going up and the ball crossing him while going down is t1. Another boy B standing on the second floor notices that time interval between the ball passing him twice (during up motion and down motion) is t2.
(a) Calculate the height difference (h) between the boy B and A.
(b) Assume that the height of boy A from the point of projection of the ball is also equal to h and calculate the speed with which the ball was projected. View SolutionQuestion 26
A stick of length L is dropped from a high tower. An ant sitting at the lower end of the stick begins to crawl up at the instant the stick is released. Velocity of the ant relative to the stick remains constant and is equal to u. Assume that the stick remains vertical during its fall, and length of the stick is sufficiently long.

(a) Calculate the maximum height attained by the ant measured from its initial position.
(b) What time after the start the ant will be at the same height from where it started?View SolutionQuestion 27
Two balls are projected simultaneously from the top of a tall building. The first ball is projected horizontally at speed u1=10m/s and the other one is projected at an angle θ=tan−1(43) to the horizontal with a velocity u2.[g=10m/s2]

(a) Find minimum value of u2(=u0) so that the velocity vector of the two balls can get perpendicular to each other at some point of time during their course of flight. ltbr? (b) Find the time after which velocities of the two balls become perpendicular if the second one was projected with speed u0. View SolutionQuestion 28
There is a large wedge placed on a horizontal surface with its incline face making an angle of 37∘ to the horizontal. A particle is projected in vertically upward direction with a velocity of u=6.5m/s from a point O on the inclined surface. At the instant the particle is projected, the wedge begins to move horizontally with a constant acceleration of a=4m/s2. At what distance from point O will the particle hit the incline surface if
(i) direction of a is along BC?
(ii) direction of a is along AB?
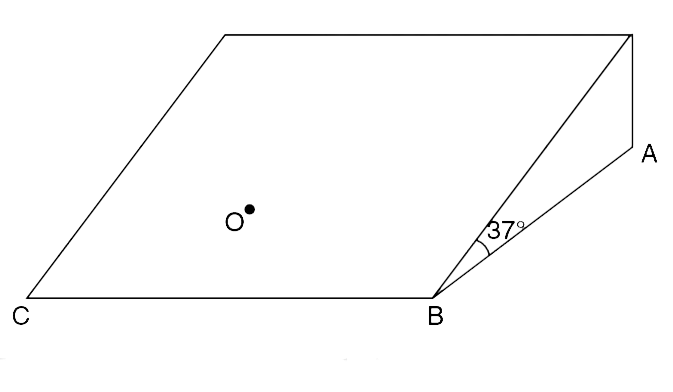 View Solution
View SolutionQuestion 29
The windshield of a truck is inclined at 37∘ to the horizontal. The truck is moving horizontally with a constant acceleration of a=5m/s2. At the instant the velocity of the truck is v0=0.77m/s, an insect jumps from point A on the windshield, with a velocity u=2.64m/s (relative to ground) in vertically upward direction. It falls back at point B on the windshield. Calculate distance AB. Assume that the insect moves freely under gravity and g=10m/s2.
 View Solution
View SolutionQuestion 30
Two persons are pulling a heavy block with the help of horizontal inextensible strings. At the instant shown, the velocities of the two persons are v1 and v2 directed along the respective strings with the strings making an angle of 60∘ between them.
(a) Find the speed of the block at the instant shown.
(b) For what ratio of v1 and v2 the instantaneous velocity of the block will be along the direction of v1.
 View Solution
View SolutionQuestion 31
A heavy block 'B' is sliding with constant velocity u on a horizontal table. The width of the block is L. There is an insect A at a distance d from the block as shown in the figure. The insect wants to cross to the opposite side of the table. It begins to crawl at a constant velocity v at the instant shown in the figure. Find the least value of v for which the insect can cross to the other side without getting hit by the block.
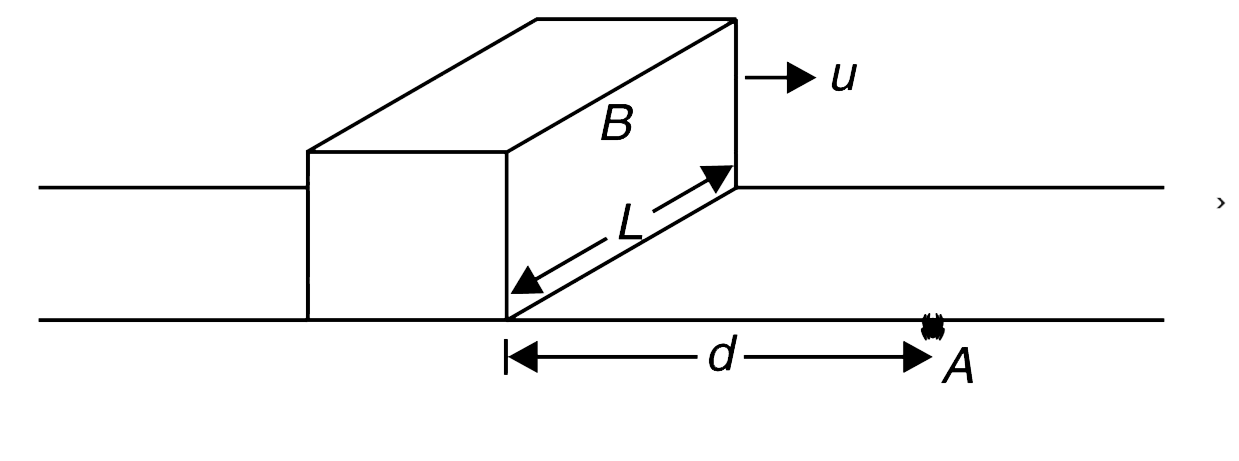 View Solution
View SolutionQuestion 32
A projectile is thrown from ground at a speed v0 at an angle α to the horizontal. Consider point of projection as origin, horizontal direction as X axis and vertically upward as Y axis. Let t be the time when the velocity vector of the projectile becomes perpendicular to its position vector.
(a) Write a quadratic equation in t.
(b) What is the maximum angle a for which the distance of projectile from the point of projection always keeps on increasing? [Hint: Start from the equation you obtained in part (a)]View Solution