A water sprinkler is positioned at O on horizontal ground. It issues water drops in every possible direction with fixed speed u. This way the sprinkler is able to completely wet a circular area of the ground (see fig). A horizontal wind starts blowing at a speed of u2√2.Mark the area on the
ground that the sprinkler will now be able to wet.
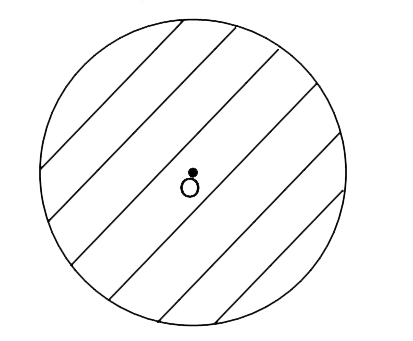
The correct Answer is:A circle of same size shifted from the original circle by ΔX=u22g in the direction of wind.
Topper's Solved these Questions
Similar Questions
_E01_216_Q01.png)
A syringe containing water is held horizontally with its nozzle at a height h above the ground as shown in fig the cross sectional areas of the piston and the nozzle are A and a respectively the piston is pushed with a constant speed v. Find the horizontal range R of the stream of water on the ground.
View Solution_E01_216_Q01.png)
A syringe containing water is held horizontally with its nozzle at a height h above the ground as shown in fig the cross sectional areas of the piston and the nozzle are A and a respectively the piston is pushed with a constant speed v. Find the horizontal range R of the stream of water on the ground.
View SolutionIn a garden a spherical sprinkler is used at the end of the lose from which the speed of the flowing water is the same to every direction. The water beam which is directed vertically upward reaches a height of h. Once the sprinkler is placed to the ground and at another time ti a height of h. By what factor will the watered area of greater in the second case ? (Neglect air resistance and consider the pressure in the sprinkler constant.)
View SolutionA wall OP is inclined to the horizontal ground at an angle α. Two particles are projected from points A and B on the ground with same speed (u) in directions making an angle θ to the horizontal (see figure). Distance between points A and B is x0=24m. Both particles hit the wall elastically and fall back on the ground. Time of flight (time required to hit the wall and then fall back on to the ground) for particles projected from A and B are 4 s and 2 s respectively. Both the particles strike the wall perpendicularly and at the same location. [In elastic collision, the velocity component of the particle that is perpendicular to the wall gets reversed without change in magnitude]
(a) Calculate maximum height attained by the particle projected from A.

(b) Calculate the inclination of the wall to the horizontal (α)[g=10m/s2]
View SolutionA canon can fire shells at speed u. Inclination of its barrel to the horizontal can be changed in steps of Δθ=1∘ ranging from θ1=15∘ to θ2=85∘. Let Rn be the horizontal range for projection angle θ=n∘.
ΔRn=|Rn−Rn+1|
For what value of n the value of ΔRn is maximum? Neglect air resistance.
(ii) A small water sprinkler is in the shape of a hemisphere with large number of uniformly spread holes on its surface. It is placed on ground and water comes out of each hole with speed u. Assume that we mentally divide the ground into many small identical patches – each having area ΔS. What is the distance of a patch from the sprinkler which receives maximum amount of water ?
View SolutionTwo guns A and B can fire bullets at speeds 1 km/s and 2 km/s respectively. From a point on a horizontal ground, they ared fired in all possible directions. The ratio of maximum areas covered by the bullets fired by the two guns, on the ground is :
View SolutionTwo guns A and B can fire bullets at speeds 1 km/s and 2 km/s respectively. From a point on a horizontal ground, they ared fired in all possible directions. The ratio of maximum areas covered by the bullets fired by the two guns, on the ground is :
View SolutionTwo guns A and B can fire bullets at speeds 1 km/s and 2 km/s respectively. From a point on a horizontal ground, they ared fired in all possible directions. The ratio of maximum areas covered by the bullets fired by the two guns, on the ground is :
View SolutionA man of mass m is standing on the flat top of a cart of mass 2m. The length and height of the cart is LandH respectively and it is at rest on a smooth horizontal ground. The man starts running from end A, speeds up and jumps out of the cart at point B with a velocity u relative to the cart in horizontal direction. Calculate the total horizontal distance covered by the man by the time he lands on the ground.
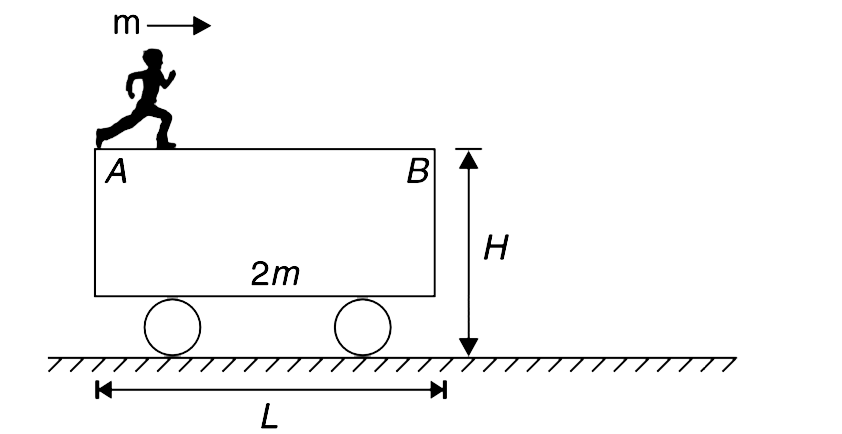
View SolutionA massive horizontal platform is moving horizontally with a constant acceleration of 10m/s2 as shown in the figure. A particle P of mass m=1kg is kept at rest at the smooth surface as shown in the figure. The particle is hinged at O
with the help of a massless rod OP of length 0.9m. Hinge O is fixed on the platform and the rod can freely rotate about point O. Now the particle P is imparted a velocity in the opposite direction of the platform's acceleration such that it is just able to complete the circular motion about point O. Then the maximum tension appearing in the rod during the motion is 10n. Find the value of n.

View Solution
