Exercise 22.2 from DC PANDEY PHYSICS (HINGLISH) CALORIMETRY & HEAT TRANSFER for Class 11
| Class 11 | PHYSICS |
| Chapter | CALORIMETRY & HEAT TRANSFER |
| DC PANDEY PHYSICS (HINGLISH) | Exercise 22.2 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 4
A lead bullet just melts when stopped by an obstacle. Assuming that 25 per cent of the heat is absorbed by the obstacle, find the velocity of the bullet if its initial temperature is 27∘C. (Melting point of lead=327∘C, specific heat of lead =0.03calories/gm/∘C, latent heat of fusion of lead=6calories/gm,J=4.2joe–s/calorie).View SolutionQuestion 7
Three liquids P,Q and R are given 4 kg of P at 60∘Cand1kgofRat50∘C when mixed produce a resultant temperature 55∘C . A mixture of 1kg of P at 60∘C and 1kg of Q at 50∘C shows a temperature of 55∘C . What will be the resulting temperature when 1 kg of Q at 60∘C is mixed with 1 kg of R at 50∘C? View SolutionQuestion 12
Three rods each of same length and cross - section are joined in series. The thermal conductivity of the materials are K, 2K and 3K respectively. If one end is kept at 200∘C and the other at 100∘C. What would be the temperature of the junctions in the steady state? Assume that no heat is lost due to radiation from the sides of the rods. View SolutionQuestion 24
Assertion : A solid sphere and a hollow sphere of same material and same radius are kept at same temperature in atmosphere. Rate of cooling of hollow sphere will be more.
Reason : If all other conditions are same, then rate of cooling is inversely proportional to the mass of body. View SolutionQuestion 29
The intensity of radiation emitted by the sun has its maximum value at a wavelength of 510nm and that emitted by the North star has the maximum value at 350nm. If these stars behave like black bodies, then the ratio of the surface temperatures of the sun and the north star is View SolutionQuestion 33
A wall has two layers A and B each made of different materials. The layer A is 10cm thick and B is 20 cm thick. The thermal conductivity of A is thrice that of B. Under thermal equilibrium temperature difference across the wall is 35∘C. The difference of temperature across the layer A is View SolutionQuestion 34
A wall has two layers A and B, each made of different material. Both the layers have the same thickness. The thermal conductivity of the material of A is twice that of B . Under thermal equilibrium, the temperature difference across the wall is 36∘C. The temperature difference across the layer A is View SolutionQuestion 35
The end of two rods of different materials with their thermal conductivities, area of cross-section and lengths all in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat in the first rod is 4cal/s. Then, in the second rod rate of heat flow in cal/s will be View SolutionQuestion 37
A lead bullet penetrates into a solid object and melts Assuming that 50% of its K.E. was used to heat it , calculate the initial speed of the bullet , The initial temp , of bullet is 27∘c and its melting point is 327∘C Latent heat of fasion of lead =2.5×104Jkg−1 and sp heat capacity of lead =1.25Jkg−1K−1View SolutionQuestion 38
A ball is dropped on a floor from a height of 2.0m. After the collision it rises up to a height of 1.5m. Assume that 40% of the mechanical energy lost goes as thermal energy into the ball.Calculate the rise in the temperature of the ball in the collision. Heat capacity of the ball is 800JK−1View SolutionQuestion 40
The emissivity of tungsten is 0.4. A tungsten sphere with a radius of 4.0 cm is suspended within a large evacuated enclosure whose walls are at 300 K. What power input is required to maintain the sphere at a temperature of 3000 K if heat conduction along supports is neglected ?
Take, σ=5.67×(10−8)Wm2−K4.View SolutionQuestion 41
A pot with a steel bottom 1.2 cm thick rests on a hot stove. The area of the bottom of the pot is 0.150m2. The water inside the pot is at 100∘Cand0.440kg are evaporated every 5.0 minute. Find the temperature of the lower surface of the pot, which is in contact with the stove. Take Lv=2.256×(106)J/kgandksteel=50.2W/m−K .View SolutionQuestion 42
A carpenter builds an outer house wall with a layer of wood 2.0 cm thick on the outside and a layer of an insulation 3.5 cm thick as the inside wall surface. The wood has K=0.08W/m−K and the insulation has K=0.01W/m−K . The interior surface temperature is 19∘C and the exterior surface temperature is −10∘C.
(a) What is the temperature at the plane where the wood meets the insulation?
(b) What is the rate of heat flow per square metre through this wall ? View SolutionQuestion 43
A closely thermally insulated vessel contains 100 g of water at 0∘C. If the air from this vessel is rapidly pumped out, intensive evaporation will produce cooling and as a result of this, water freeze. How much ice will be formed by this method? If latent heat of fusion is 80cal/g and of evaporation 560cal/g .
[ Hint If m gram ice is formed, mLf=(100−m)lv]View SolutionQuestion 45
A certain amount of ice is supplied heat at a constant rate for 7 minutes. For the first one minute the temperature rises uniformly with time. Then, it remains constant for the next 4 minute and again the temperature rises at uniform rate for the last two minutes. Calculate the final temperature at the end of seven minutes.
(Given, L of ice =336×(103)J/kg and specific heat of water =4200J/kg−K).View SolutionQuestion 46
Four identical rods AB,CD,CFandDE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l,AandK respectively. The ends A,EandF are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.
 View Solution
View SolutionQuestion 47
The ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.View SolutionQuestion 48
A copper sphere is suspended in an evacuated chamber maintained at 300K. The sphere is maintained at a constant temperature of 500K by heating it electrically. A total of 210W of electric power is needed to do it. When the surface of the copper sphere is completely blackened, 700W is needed to maintain the same temperature of the sphere. Calculate the emissivity of copper.View SolutionQuestion 49
A cylindrical rod with one end in a steam chamber and the other end in ice results in melting of 0.1 g of ice per second. If the rod is replaced by another with half the length and double the radius of the first and if the thermal conductivity of material of second rod is 1/4 that of first, the rate at which ice melts in g/s will be View SolutionQuestion 50
Two sheets of thickness d and 3d, are touching each other. The temperature just outside the thinner sheet is T1 and on the side of the thicker sheet is T3. The interface temperature is T2.T1,T2andT3 are in arithmetic progression. The ratio of thermal conductivity of thinner sheet to thicker sheet isView SolutionQuestion 51
A long rod has one end at 0∘C and other end at a high temperature. The coefficient of thermal conductivity varies with distance from the low temperature end as K=K0(1+ax), where K0=102 SI unit and a=1m−1 . At what distance from the first end the temperature will be 100∘C? The area of cross-section is 1cm2 and rate of heat conduction is 1 W. View SolutionQuestion 53
Three rods of identical cross-sectional area and made from the same metal form the sides of an isosceles triangle ABC right angled at B as shown in the figure. The points A and B are maintained at temperature T and (√2)T respectively in the steady state. Assuming that only heat conduction takes place, temperature of point C will be
 View Solution
View SolutionQuestion 55
The temperature of the two outer surfaces of a composite slab consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab in steady state is (AK(T2−T1)x)f. where, f is equal to
 .View Solution
.View SolutionQuestion 61
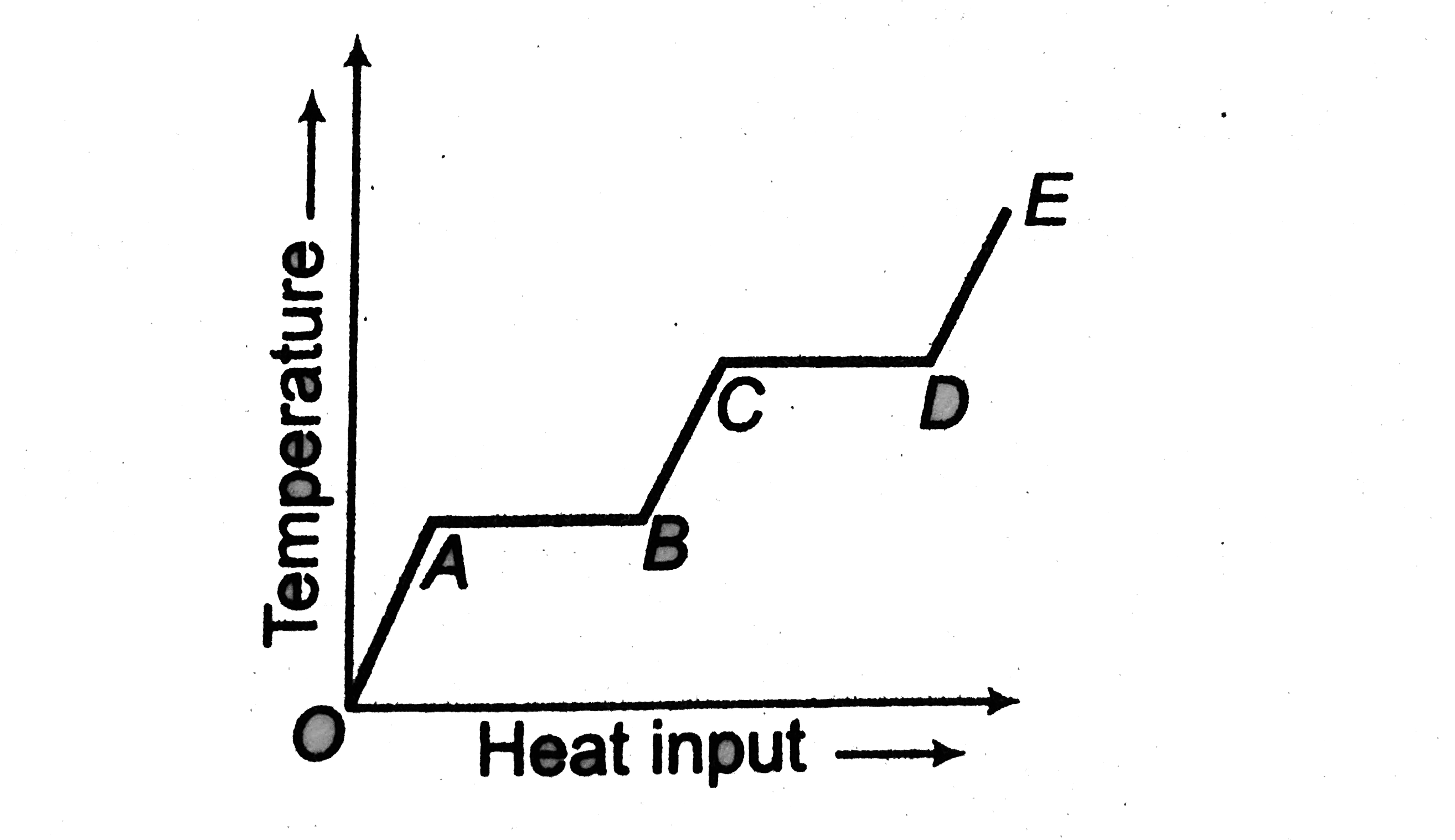
As a physicist, you put heat into a 500 g solid sample at the rate of 10.0kJ/min, while recording its temperature as a function of time. You plot your data and obtain the graph shown in figure.
 .
.
(a) What is the latent heat of fusion for this solid?
(b) What is the specific heat of solid state of the material? View SolutionQuestion 63
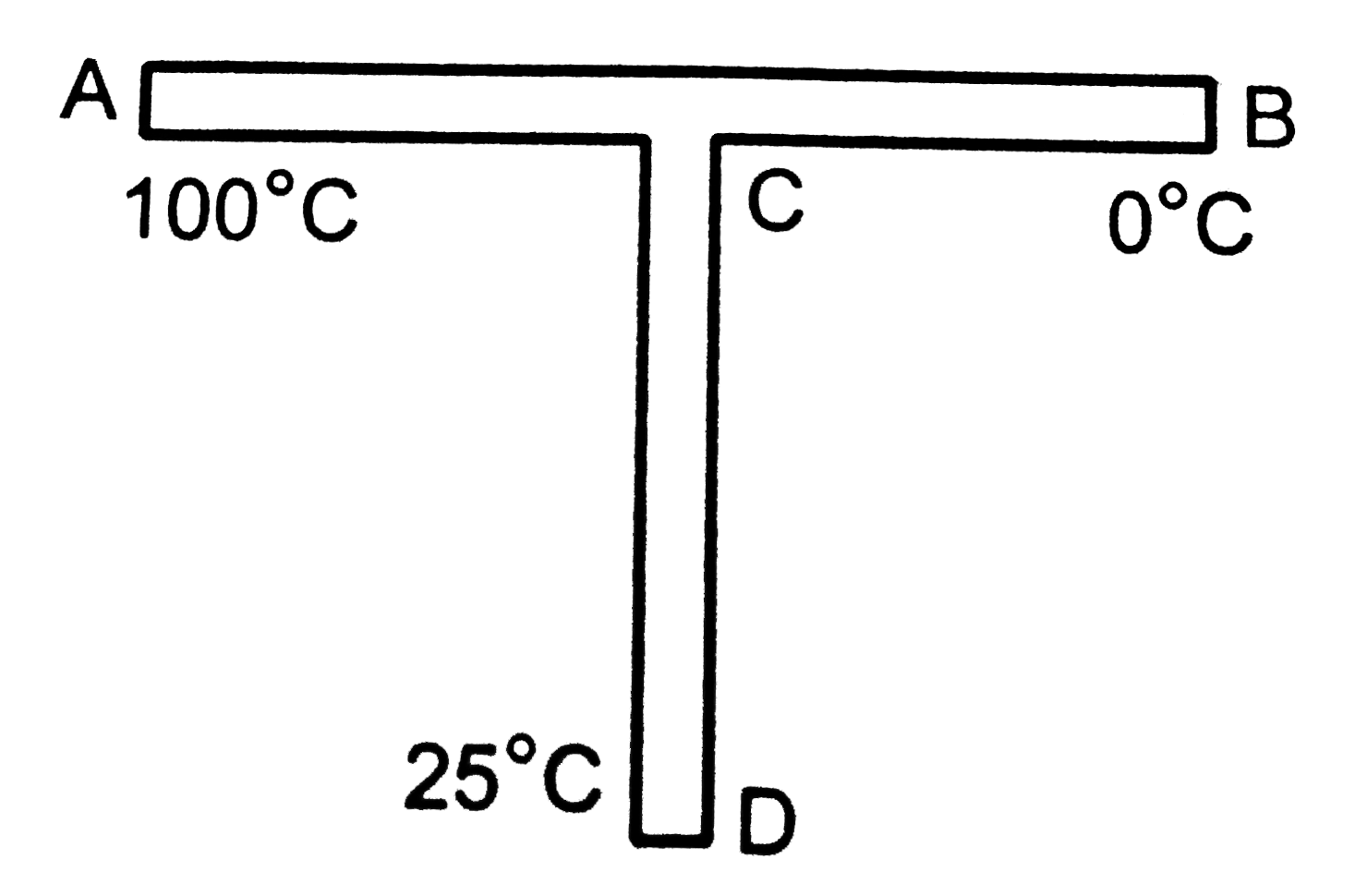
Three rods of copper, brass and steel are welded together to form a Y -shaped structure. The cross-sectional area of each rod is 4cm2. The end of copper rod is maintained at 100∘C and the ends of the brass and steel rods at 80∘C and 60∘C respectively. Assume that there is no loss of heat from the surfaces of the rods. The lengths of rods are : copper 46 cm, brass 13 cm and steel 12 cm.
(a) What is the temperature of the junction point?
(b) What is the heat current in the copper rod?
K(copper) = 0.92, K (steel) = 0.12 and K(brass) = 0.26 cal/cm−s∘C .View SolutionQuestion 64
Ice at 0∘C is added to 200 g of water initially at 70∘C in a vacuum flask. When 50 g of ice has been added and has all melted the temperature of the flask and contents is 40∘C. When a further 80 g of ice has been added and has all melted the temperature of the whole becomes 10∘C. Find the latent heat of fusion of ice. View SolutionQuestion 65
A copper cube of mass 200g slides down an a rough inclined plane of inclination 37∘ at a constant speed. Assume that any loss in mechanical energy goes into the copper block as thermal energy .Find the increase in the temperature of the block as it slides down through 60cm. Specific heat capacity of copper =420Jkg−1K−1View SolutionQuestion 66
A cylindrical block of length 0.4 m and area of cross-section 0.04m2 is placed coaxially on a thin metal disc of mass 0.4 kg and of the same cross - section. The upper face of the cylinder is maintained at a constant temperature of 400 K and the initial temperature of the disc is 300K. if the thermal conductivity of the material of the cylinder is 10watt/m−K and the specific heat of the material of the disc is 600J/kg−K, how long will it take for the temperature of the disc to increase to 350 K? Assume for purpose of calculation the thermal conductivity of the disc to be very high and the system to be thermally insulated except for the upper face of the cylinder. View SolutionQuestion 67
A metallic cylindrical vessel whose inner and outer radii are r1andr2 is filled with ice at 0∘C. The mass of the ice in the cylinder is m. Circular portions of the cylinder is sealed with completely adiabatic walls. The vessel is kept in air. Temperature of the air is 50∘C. How long will it take for the ice to melt completely. Thermal conductivity of the cylinder is K and its length is l. Latent heat of fusion of L. View SolutionQuestion 68
An electric heater is placed inside a room of total wall area 137m2 to maintain the temperature inside at 20∘C. The outside temperature is −10∘C. The walls are made of three composite materials. The inner most layer is made of wood of thickness 2.5 cm the middle layer is of cement of thickness 1 cm and the exterior layer is of brick of thickness 2.5 cm. Find the power of electric heater assuming that there is no heat losses through the floor and ceiling. The thermal conductivities of wood, cement and brick are 0.125W/m∘−C,1.5W/m∘−Cand1.0W/m∘−C respectively. View SolutionQuestion 69
A 2 m long wire of resistance 4Ω and diameter 0.64 mm is coated with plastic insulation of thickness 0.66 mm. A current of 5A flows through the wire. Find the temperature difference across the insulation in the steady state. Thermal conductivity of plastic is 0.16×(10−2)cal/scm∘−C.View SolutionQuestion 70
Two bodies of masses m1 and m2 and specific heat capacities S1 and S2 are connected by a rod of length l, cross-section area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time t=0 , the temperature of the first body is T1 and the temperature of the second body is T2(T2>T1) . Find the temperature difference between the two bodies at time t. View SolutionQuestion 71
A rod of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as k=a/T, where a is a constant. The ends of the rod are kept at temperatures T1andT2. Find the function T(x), where x is the distance from the end whose temperature is T1. View SolutionQuestion 72
One end of a uniform brass rod 20 cm long and 10cm2 cross-sectional area is kept at 100∘C. The other end is in perfect thermal contact with another rod of identical cross-section and length 10 cm. The free end of this rod is kept in melting ice and when the steady state has been reached, it is found that 360 g of ice melts per hour. Calculate the thermal conductivity of the rod, given that the thermal conductivity of brass is 0.25cal/scm∘CandL=80cal/g.View SolutionQuestion 74
A layer of ice of thickness y is on the surface of a lake. The air is at a constant temperature −θ∘C and the ice water interface is at 0∘C. Show that the rate at which the thickness increases is given by
dydt=KθLρy
where, K is the thermal conductivity of the ice, L the latent heat of fusion and ρ is the density of the ice. View Solution
 .
.