Exercise 7.1 from DC PANDEY PHYSICS (HINGLISH) PROJECTILE MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | PROJECTILE MOTION |
| DC PANDEY PHYSICS (HINGLISH) | Exercise 7.1 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 12
The coach throws a baseball to a player with an initial speed of 20m/s at an angle of 45∘ with the horizontal. At the moment the ball is thrown, the player is 50 m from the coach. At what speed and in what direction must the player run to catch the ball at the same height at which it was released? (g=10m/s2).View SolutionQuestion 13
A ball is thrown horizontally from a point 100m above the ground with a speed of 20m/s. Find (a) the time it takes to reach the ground, (b) the horizontal distance it travels before reaching the ground, (c) the velocity (direction and magnitude) with which it strikes the ground. View SolutionQuestion 20
A particle is projected upwards with velocity 20m/s. Simultaneously another particle is projected with velocity 20(√2)m/s at 45∘. (g=10m/s2)
(a) What is acceleration of first particle relative to the second?
(b) What is initial velocity of first particle relative to the other?
(c) What is distance between two particles after 2 s?View SolutionQuestion 28
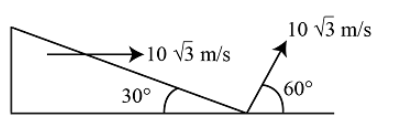
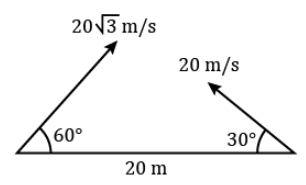
Assertion : Particle A is projected upwards. Simultaneously particle B is projected as projectile as shown. Particle A returns to ground in 4s. At the same time particle B collides with A. Maximum height H attained by B would be 20 m. (g=10ms−2) .
Reason : Speed of projectile of both the particles should be same under the given condition.
 .View Solution
.View SolutionQuestion 45
A body is projected at time t=0 from a certain point on a planet's surface with a certain velocity at a certain angle with the planet's surface (assumed horizontal). The horizontal and vertical displacement x and y (in metre) respectively vary with time t in second as, x=(10√3)tandy=10t−t2. The maximum height in meter attained by the body is View SolutionQuestion 47
A fixed mortar fires a bomb at an angle of 53∘ above the horizontal with a muzzle velocity of 80ms−1. A tank is advancing directly towards the mortar on level ground at a constant speed of 5m/s. The initial separation (at the instant mortar is fired) between the mortar and tank, so that the tank would be hit is [Takeg=10ms−2]View SolutionQuestion 52
Two particles move in a uniform gravitational field with an acceleration g. At the initial moment the particles were located over a tower at one point and moved with velocities v1=3m/sandv2=4m/s horizontally in opposite directions. Find the distance between the particles at the moment when their velocity vectors become mutually perpendicular. View SolutionQuestion 57
Two particles A and B are projected simultaneously from two towers of heights 10 m and 20m respectively. Particle A is projected with an initial speed of 10√2m/s at an angle of 45∘ with horizontal, while particle B is projected horizontally with speed 10m/s. If they collide in air, what is the distance d between the towers?
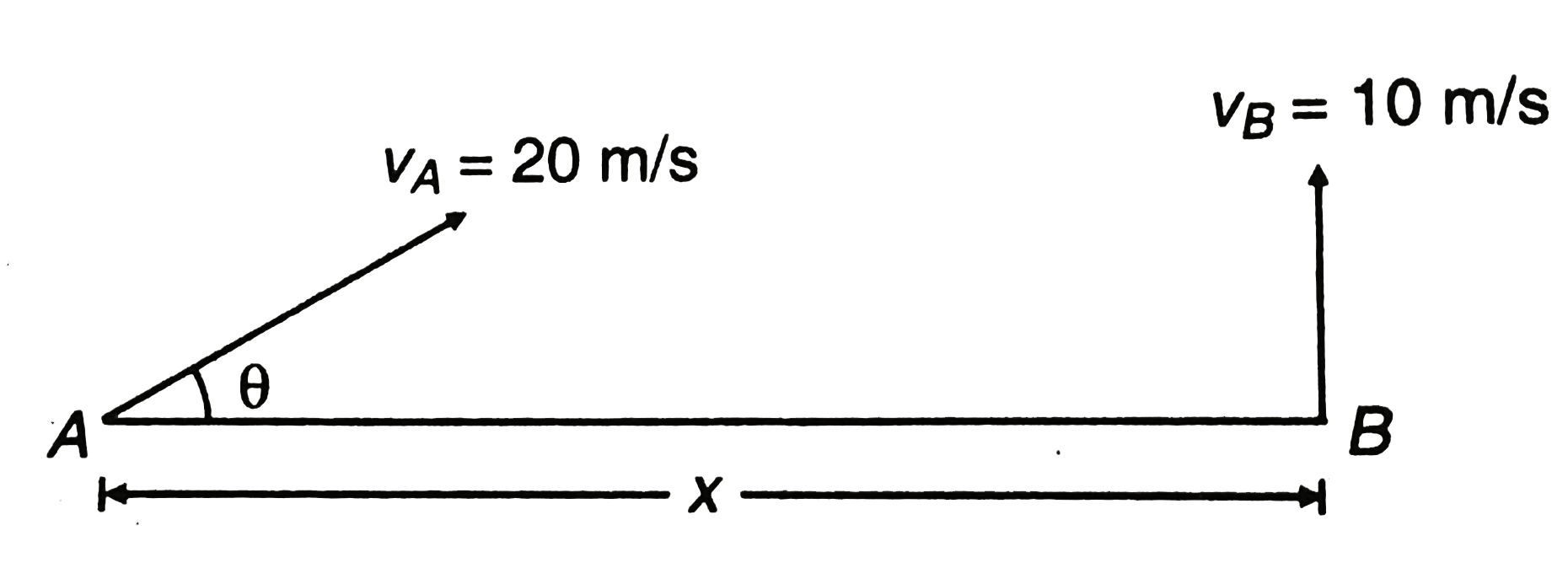 View Solution
View SolutionQuestion 60
A ball is shot from the ground into the air. At a height of 9.1 m, its velocity is observed to be v=7.6ˆi+6.1ˆj in metre per second (ˆi is horizontal, ˆj is upward). Give the approximate answers.
(a) To what maximum height does the ball rise?
(b) What total horizontal distance does the ball travel?
(c) What are the magnitude and
(d) What are the direction of the ball's velocity just before it hits the ground? View SolutionQuestion 63
A projectile aimed at a mark, which is in the horizontal plane through the point of projection, falls a cm short of it when the elevation is α and goes b cm far when the elevation is β. Show that, if the speed of projection is same in all the cases the proper elevation is
12sin−1[bsin2α+asin2βa+b] .View SolutionQuestion 64
Two particles are simultaneously thrown in horizontal direction from two points on a riverbank, which are at certain height above the water surface. The initial velocities of the particles are v1=5m/sandv2=7.5m/s respectively. Both particles fall into the water at the same time. First particles enters the water at a point s = 10 m from the bank. Determine
(a) the time of flight of the two particles,
(b) the height from which they are thrown,
(c) the point where the second particle falls in water. View SolutionQuestion 65
A ballon is ascending at the rate v=12km/h and is being carried horizontally by the wind at vw=20km/h. If a ballast bag is dropped from the balloon at the instant h = 50 m, determine the time needed for it to strike the ground. Assume that the bag was released from the ballon with the same velocity as the balloon. Also, find the speed with which the bag strikes the ground? View SolutionQuestion 67
An elecator is going up with an upward acceleration of 1m/s2. At the instant when its velocity is 2m/s, a stone is projected upward from its floor with a speed of 2m/s relative to the elevator, at an elevation of 30∘.
(a) Calculate the time taken by the stone to return to the floor.
(b) Sketch the path of the projectile as observed by an observer outside the elevator.
(c) If the elevator was moving with a downward acceleration equal to g, how would the motion be altered? View SolutionQuestion 79
Two particles projected form the same point with same speed u at angles of projection αandβ strike the horizontal ground at the same point. If h1andh2 are the maximum heights attained by the projectile, R is the range for both and t1andt2 are their times of flights, respectively, then View SolutionQuestion 85
Two inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.
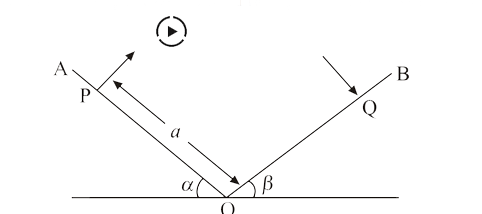
If α=30∘,β=30∘ the time of flight from P to Q is View SolutionQuestion 86
Two inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.
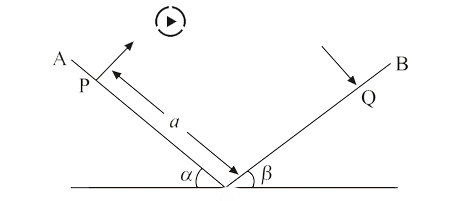
If α=30∘,β=30∘ and a = 4.9 m, the initial velocity of projection is View SolutionQuestion 87
Determine the horizontal velocity v0 with which a stone must be projected horizontally from a point P, so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is θ and point P is at a height h above the foot of the incline, as shown in the figure.
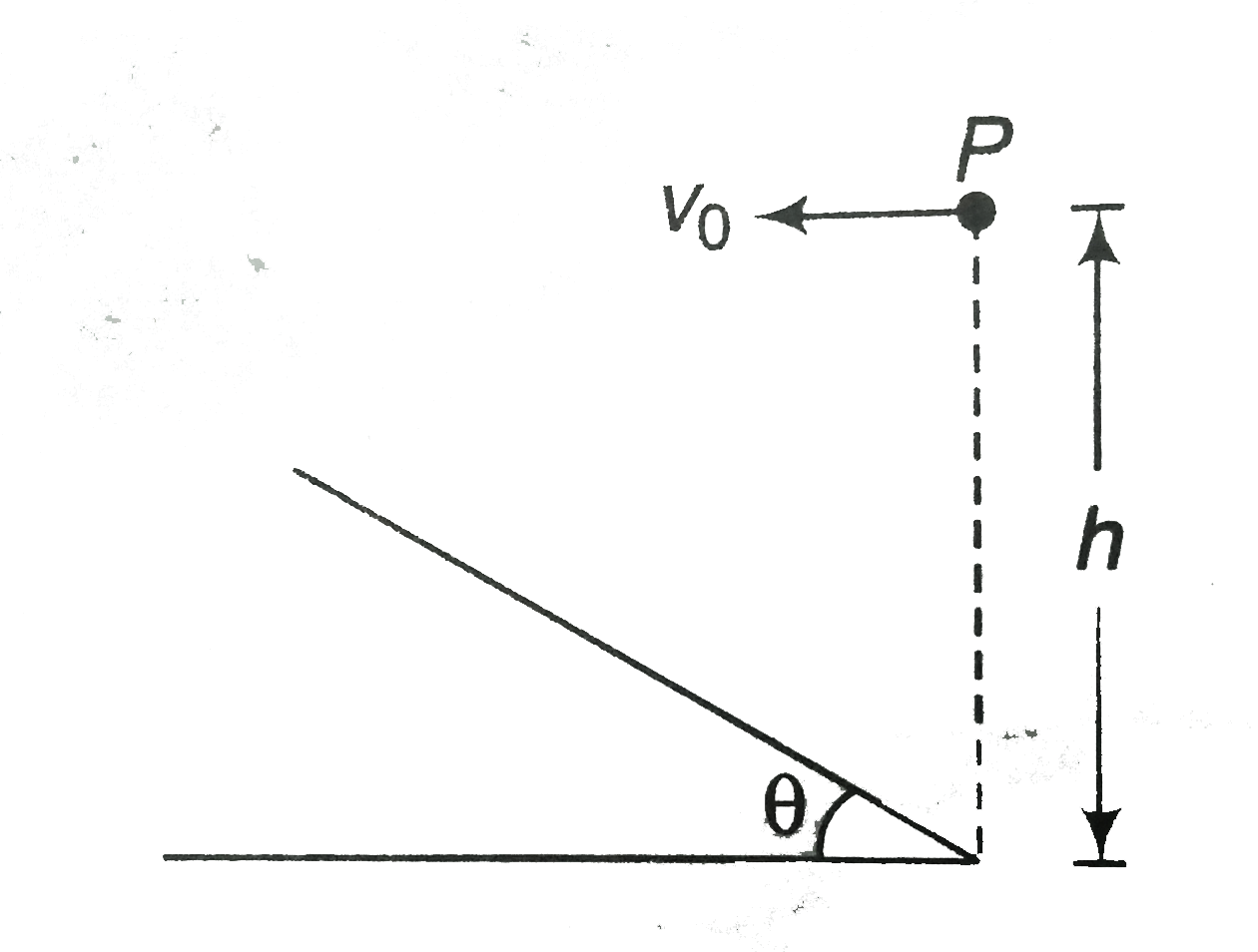 View Solution
View SolutionQuestion 88
A particle is dropped from point P at time t = 0. At the same time another particle is thrown from point O as shown in the figure and it collides with the particle P. Acceleration due to gravity is along the negative y-axis. If the two particles collide 2 s after they start, find the initial velocity v0 of the particle which was projected from O. Point O is not necessarily on ground.
 View Solution
View SolutionQuestion 90
A projectile takes off with an initial velocity of 10m/s at an angle of elevation of 45∘. It is just able to clear two hurdles of height 2 m each, separated from each other by a distance d. Calculate d. At what distance from the point of projection is the first hurdle placed? Take g=10m/s2. View SolutionQuestion 91
A stone is projected from the ground in such a direction so as to hit a bird on the top of a telegraph post of height h and attains the maximum height of 2h above the ground. If at the insatant of projection, the bird were to fly away horizontally with a uniform speed, find the ratio between the horizontal velocity of bird and the horizontal component of velocity of stone, if the stone hits the bird while descending. View SolutionQuestion 92
A particle is released from a certain height H=400m. Due to the wind, the particle gathers the horizontal velocity component vx=aywhere a =(√5)s−1 and y is the vertical displacement of the particle from the point of release, then find
(a) the horizontal drift of the particle when it strikes the ground ,
(b) the speed with which particle strikes the ground. View SolutionQuestion 93
A train is moving with a constant speed of 10m/s in a circle of radius 16πm. The plane of the circle lies in horizontal x-y plane. At time t = 0, train is at point P and moving in counter- clockwise direction. At this instant, a stone is thrown from the train with speed 10m/s relative to train towards negative x-axis at an angle of 37∘ with vertical z-axis . Find
(a) the velocity of particle relative to train at the highest point of its
trajectory.
(b) the co-ordinates of points on the ground where it finally falls and that of the hightest point of its trajectory. (Take g =10m/s2,sin37∘=35
 View Solution
View SolutionQuestion 94
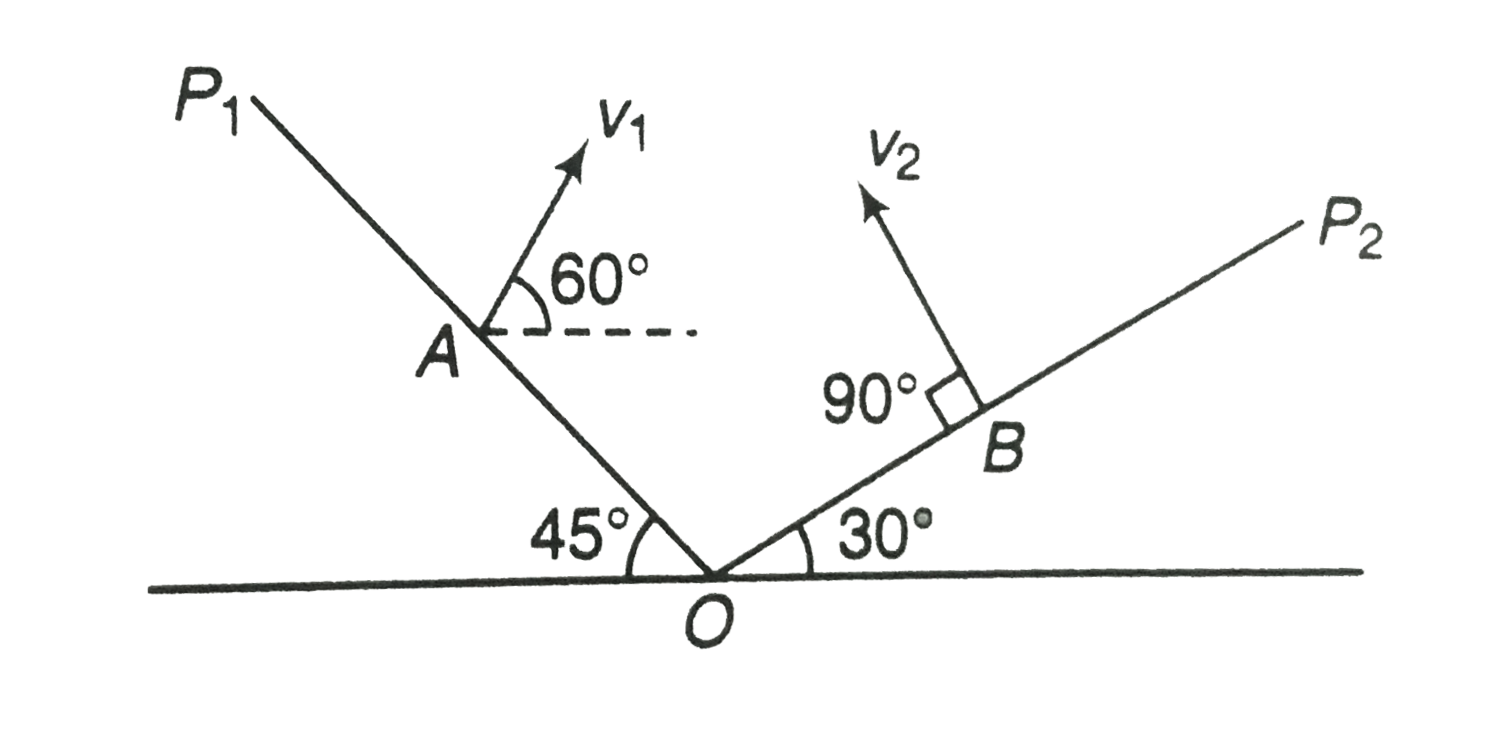
A particle is projected from an inclined plane OP1 from A with velocity v1=8ms−1 at an angle 60∘ with horizontal. An another particle is projected at the same instant from B with velocity v2=16ms−1 and perpendicular to the plane OP2 as shown in figure. After time 10(√3) s there separation was minimum and found to be 70m. Then find distance AB.
 View Solution
View SolutionQuestion 95
A particle is projected from point O on the ground with velocity u=5(√5)m/s at angle α=tan−1(0.5). It strikes at a point C on a fixed smooth plane AB having inclination of 37∘ with horizontal as shown in figure. If the particle does not rebound, calculate.
(a) coordinates of point C in reference to coordinate system as shown in the figure.
(b) maximum height from the ground to which the particles rises. (g=10m/s2)
 View Solution
View SolutionQuestion 96
A plank fitted with a gun is moving on a horizontal surface with speed of 4m/s along the positive x-axis. The z-axis is in vertically upward direction. The mass of the plank including the mass of the gun is 50 kg. When the plank reaches the origin, a shell of mass 10 kg is fired at an angle of 60∘ with the positive x-axis with a speed of v=20m/s with respect to the gun in x-z plane. Find the position vector of the shell at t=2 s after firing it. Take g=9.8m/s2.View Solution


 .
.  .
.