Type A Worked out examples from DHANPAT RAI & CO PHYSICS (HINGLISH) OSCILLATIONS for Class 11
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| DHANPAT RAI & CO PHYSICS (HINGLISH) | Type A Worked out examples |
| Medium | English |
| Academic Year | 2023-2024 |
Question 3
The motion of a particle in S.H.M. is described by the displacement function, x=Acos(ωt+ϕ), If the initial (t=0) position of the particle is 1cm and its initial velocity is ωcms−1, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs−1. If instead of the cosine function, we choose the sine function to describe the SHM:x=Bsin(ωt+α), what are the amplitude and initial phase of the particle with the above initial conditions ?View SolutionQuestion 4
The motion of a particle in S.H.M. is described by the displacement function, x=Acos(ωt+ϕ), If the initial (t=0) position of the particle is 1cm and its initial velocity is ωcms−1, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs−1. If instead of the cosine function, we choose the sine function to describe the SHM:x=Bsin(ωt+α), what are the amplitude and initial phase of the particle with the above initial conditions ?View SolutionQuestion 9
Time period of a simple pendulum is 2s and it can go to and fro from equilibrium position at a maximum distance of 6cm. If at the start of the motion the pendulum is in the position of maximum displacement towards the right of the equilibrium position, then write the displacement equation of the pendulum. View SolutionQuestion 23
A partical executes SHM on a straigh line path. The amplitude of oscillation is 2cm. When the displacement of the particle from the mean position is 1cm, the magnitude of its acceleration is equal to that of its velocity. Find the time period of SHM, also the ms. velocity and ms. acceleration of SHM. View SolutionQuestion 24
A person normally weighing 60kg stands on a platform which oscillates up and down harmonically at a frequency 2.0sec−1 and an amplitude 5.0cm . If a machine on the platform gives the person's weight against time deduce the maximum and minimum reading it will shown, Takeg=10m/sec2.View SolutionQuestion 30
A spring compressed by 0.2 m develops a restoring force of 25 N. A body of mass 5 kg is placed over it. Deduce (i) force constant of the spring (ii) the depression of the spring under the weight of the body and (iii) the period of oscillation, if the body is disturbed. Take g=10Nkg−1.View SolutionQuestion 32
A body of mass 12 kg is suspended by a coil spring of natural length 50 cm and force constant 2.0×10Nm−1. What is the stretched length of the spring ? If the body is pulled down further stretching the spring to a length of 59 cm and then released, what is the frequency of oscillation of the suspended mass ? (Neglect the mass of the spring).View SolutionQuestion 34
A spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.
View SolutionQuestion 35
In example 34, let us take the position of the mass, when the spring is unstretched, as x=0, and the direction from left to right as the positive direction of X-axis. Give x as a function of time t for the oscillating mass, if at the moment we start the stop watch (t=0), the mass is (i) at the mean position (ii) at the maximum stretched position (iii) at the maximum compressed position.
In what do these different functions of SHM differ ? Frequency, amplitude or initial phase ?View SolutionQuestion 37
A 2.5 kg collar attached to a spring of foce constant 1000 Nm−1 slides without friction on a horizontal rod. The collar is displaced from its equilibrium position by 5.0 cm and released. Calculate (i) the period of oscillation (ii) the maximum speed of the collar and (iii) the maximum acceleration of the collar.View SolutionQuestion 38
A small trolley of mass 2.0 kg resting on a horizontal turn table is connected by a light spring to the centre of the table. When the turn table is set into rotation at a speed of 300 rpm, the length of the stretched spring is 40 cm. If the original length of the spring is 35 cm, determine the force constant of the spring.View SolutionQuestion 40
four different springs arrangements. If the mass m in each arrangement is displaced from its equilibrium position and released, what is the resulting frequency of vibration in each case? Neglect the mass of the spring. Figure (a) and (b) represent an arrangement of springs in parallel and (c) and (d) represent springs in series?
View SolutionQuestion 42
Figure a) shows a spring of force constant k clamped rigidly at once end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?
View SolutionQuestion 43
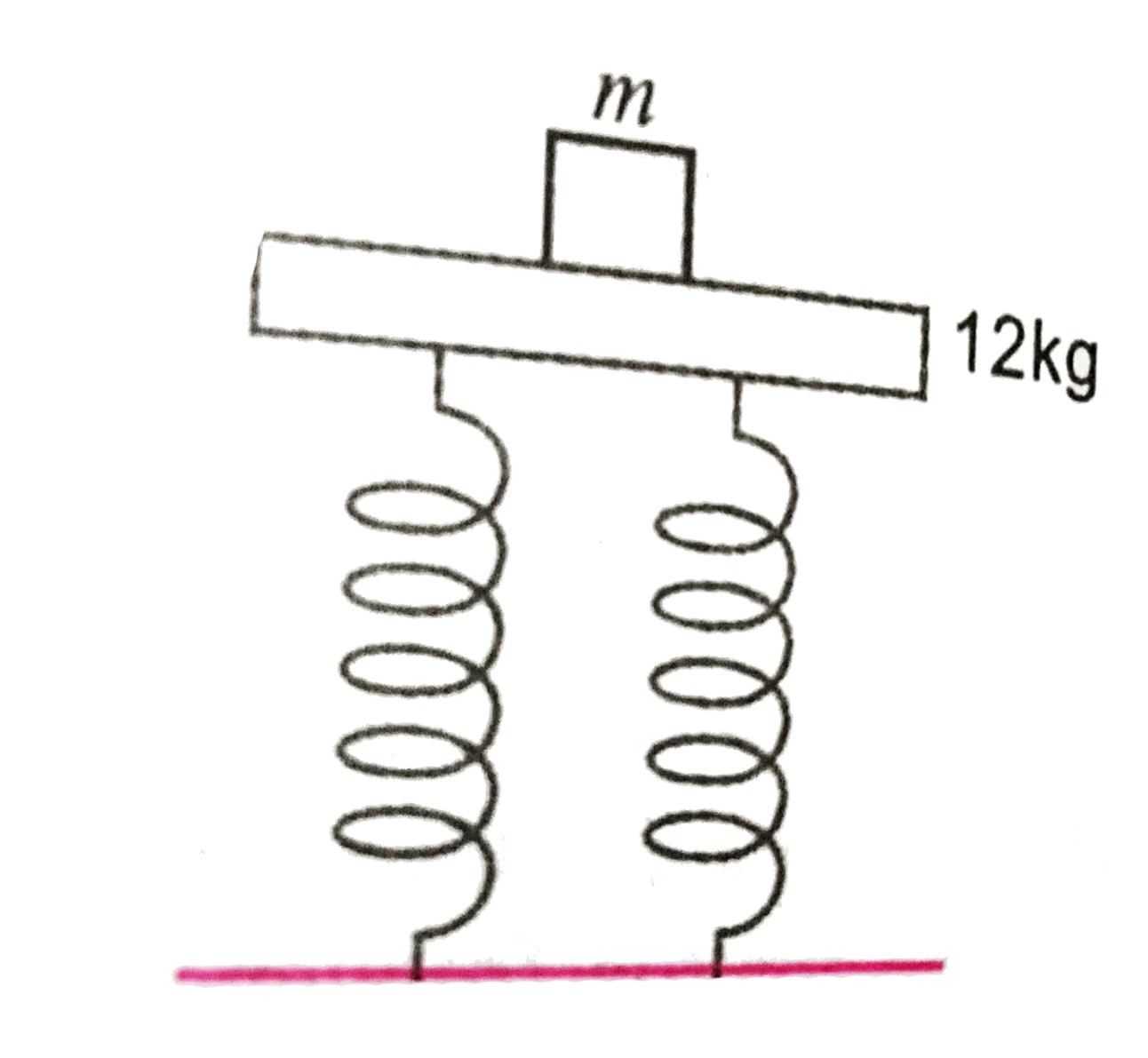
A tray of mass 12 kg is supported by two identical springs as shown in figure. When the tray is pressed down slightly and released, it executes SHM with a time period of 1.5s. What is the force constant of each spring?When a block of mass m is placed on the tray , the period of SHM changes to 3.0s. What is the mass of the block ?
View SolutionQuestion 44
A tolley of mass 3.0kg is connected to two identical spring each of force constant 600Nm−1 as shown in figure. If the trolley is displaced from its equilibrium position by 5.0 cm and released, what is
(a) the period of ensuing oscillation?
(b) the maximum speed of trolley?
(c) How much is the total energy dissipated as heat by the time the trolley comes to rest due to damping forces?
View SolutionQuestion 47
Calculate the percentage change in the time period of a simple pendulum, if (i) the length of the pendulum be increased by 4% (ii) the mass of the bob be increased by 30% (iii) the oscillation amplitude be decreased by 40% and (iv) the pendulum be taken to a place where the value where the value of g be 0.8% more.View SolutionQuestion 55
An air chamber of volume V has a neck area of cross section A into which a ball of mass m just fits and can move up and down without any friction, figure. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure volume variations of air to be isothermal. View SolutionQuestion 58
A cylinderical wooden block of cross-section 15.0 cm2 and mass 230g is floated over water with an extra weight of 50 g attached to its bottom. The cylider floats vertically. From the state of equilibrium, it is slightly depressed and released. If the specific gravity of wood is 0.30 and g=9.8ms−2 deduce the frequency of the block, A=15.0cm2=15×10−4m2View SolutionQuestion 61
A circular disc of mass 10kg is suspended by a wire attahced to its centre. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be 1.5s. The radius of the disc is 15cm. Determing the torsional spring constant of the wire. (Torsional spring constant α is definied by the relation J=−αθ, where J is the restoring coubple and θ the angle of twist.View SolutionQuestion 77
A block is kept on a horizontal table. The table is undergoing simple farmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friction between the block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface g=10ms−1View SolutionQuestion 83
A body of mass 1.0 kg is suspended from a weightless spring having force constant 600Nm−1. Another body of mass 0.5 kg moving vertically upwards hits the suspended body with a velocity of 3.0ms−1 and gets embedded in it. Find the frequency of oscillations and amplitude of motion.View SolutionQuestion 85
A certain spring stretches 25 cm when a 500 g mass is hung from its end. It is now used as shown in fig. With 2 kg mass at one end placed on a frictionless surface. Suppose the mass is pulled to the right until the spring is stretched to 10 cm and then released. find the speed with which the mass moves through the unstretched position.
View SolutionQuestion 86
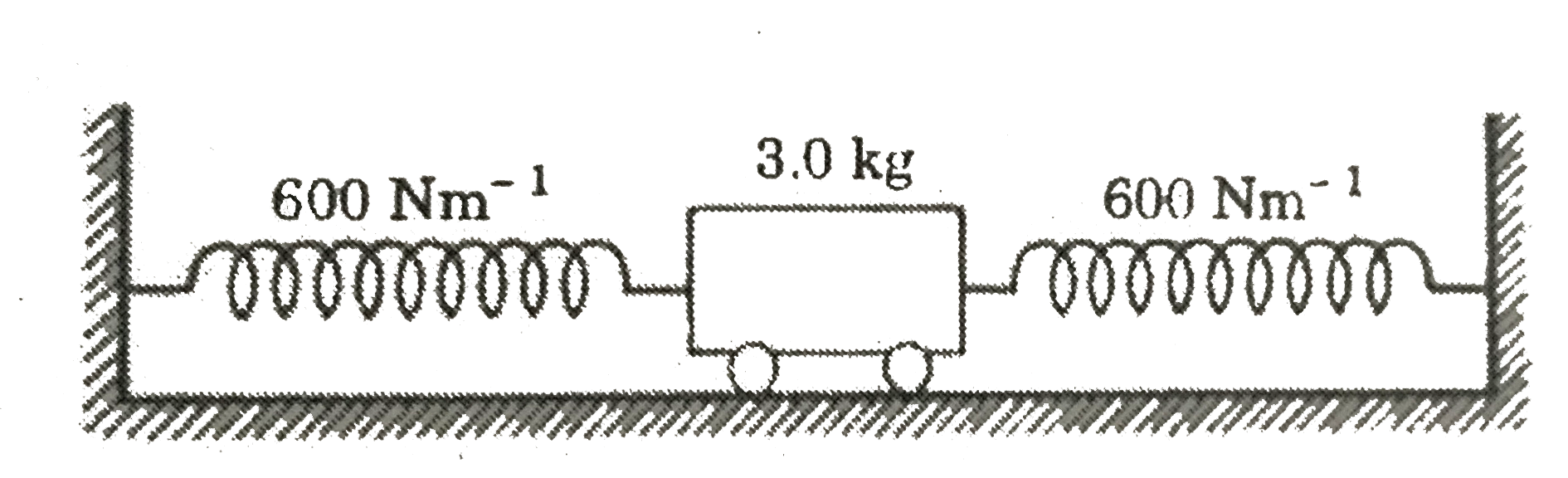
Two bodies of masses 1 kg and 3 kg respectively are connected rigidly by a vertcal spring. The body of mass 3 kg rests on a smototh horizontal surface. The force constant of the spring is 484Nm−1. From the equilibrium position, the mass of 1 kg is displaced vertically through a distance of 0.02 m and then released. calculate (i) and frequency of oscillation of the mass of 1 kg (ii) the maximum velocity of this mass (iii) its oscillation energy and (iv) the reaction of the table on the mass of 3 kg, when mass 1 kg is having harmonic oscillations.
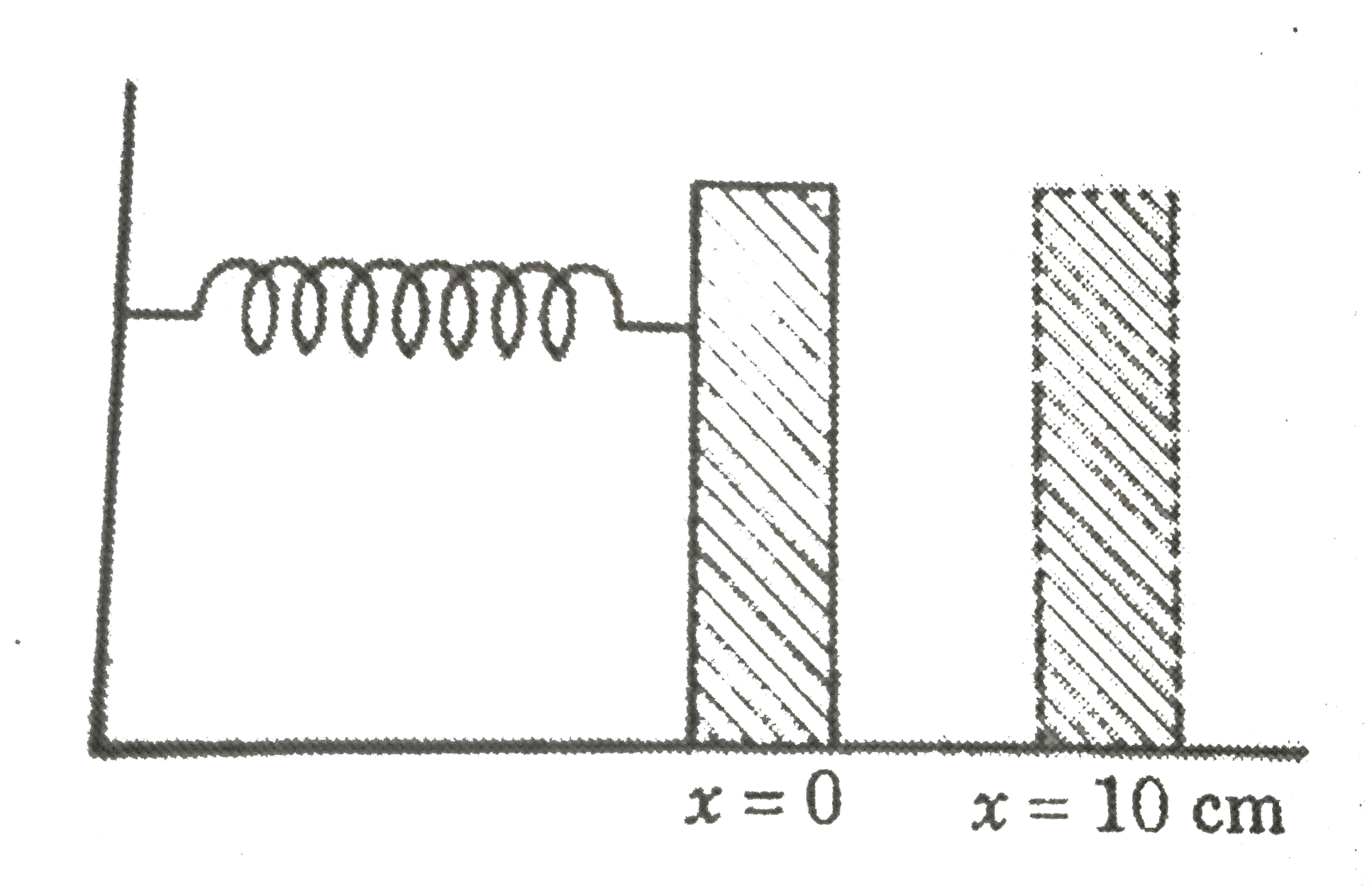View SolutionQuestion 89
A uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.View SolutionQuestion 90
One end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :View SolutionQuestion 91
Two identical balls (A) and (B) each of mass (0.1 kg), are attached to two identical massless springs. The spring - mass system is constrained to move inside a riged smooth pipe bant in the form of a circle as shown in Fig. The pipe is fixed in a horizontal plane.
The centres of the balls can move in a circle of radius (0.06 pi) meter. Each spring has a natural length zof0.06π meter and spring spring constant5 0.1N/m. Initially, both the balls are displaced by an angle θ=π/6 radian with respect to the diameter (pQ) of the circle (as shown in Fig.) and released from, rest.
.
(i) Calculate the frequency of oscillation of ball (B).
(ii) Find the speed of ball (A) when (A) and (B) are at the two ends of the diameter (PQ).
(iii) What is the total energy of the system.View SolutionQuestion 92
A thin rod of length (L) and area of cross - section (S) is pivoted at its lowest point (P) inside a stationary, homegeneous and non - viscous liquid. The rod is free to ratate in a vertical plane about a horizontal axis passing through (P). The density (d_1) of the material of the rod is smaller than the density (d_2) of the liquid. The rod is displaced by a small angle (theta) from its equilibrium position and then released. Show that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters.
.View Solution