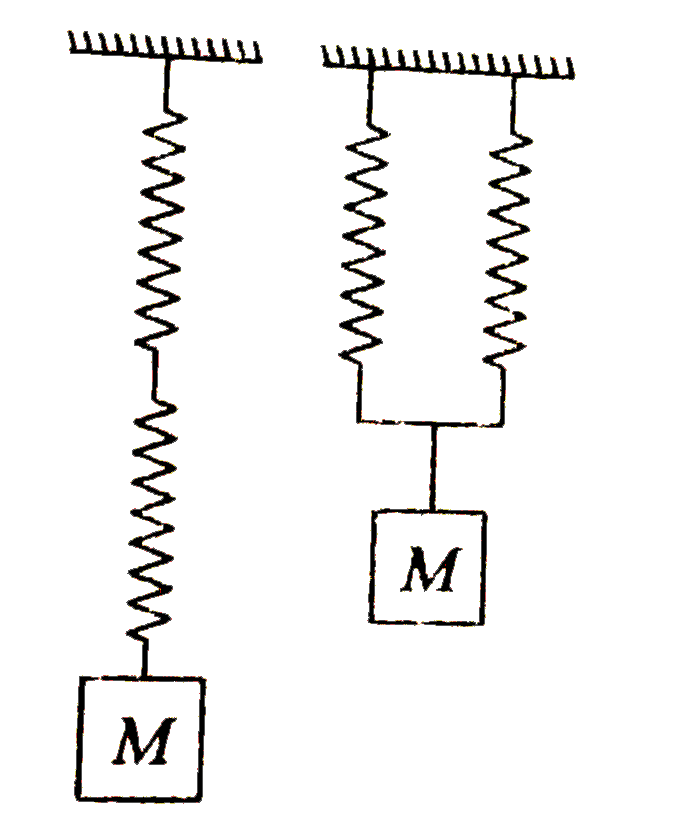Exercise from DHANPAT RAI & CO PHYSICS Chapter 15 OSCILLATIONS for Class 11
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| DHANPAT RAI & CO PHYSICS | Exercise |
| Medium | English |
| Academic Year | 2023-2024 |
Question 10
A particle executing SHM completes 1200 oscillations per minute and passes through the mean position with a velocity of 31.4ms−1. Determine the maximum displacement of the particle from the mean position also obtain the displacement equation of the aprticle if its displacemet be zero at the instant t=0.View SolutionQuestion 14
A partical executes SHM on a straigh line path. The amplitude of oscillation is 2cm. When the displacement of the particle from the mean position is 1cm, the magnitude of its acceleration is equal to that of its velocity. Find the time period of SHM, also the ms. velocity and ms. acceleration of SHM. View SolutionQuestion 23
A man stands on a weighing machine placed on a horizontal platform the machine reads 50kg. By mean of a suitable mechanism, the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibration per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of platform is 5cm. Take g=10ms−2 View SolutionQuestion 28
A particle which is attached to a spring oscillates horizontally with simple harmonic motion with a frequency of 1/π Hz and total energy of 10J. If the maximum speed of the particle is 0.4ms−1, what is the force constant of the spring? What will be the maximum potential energy of the spring during the motion? View SolutionQuestion 29
A spring compressed by 0.1m develops a restoring force 10N. A body of mass 4kg is placed on it. Deduce (i) the force constant of the spring (ii) the depression of the spring under the weight of the body ( take g=10N/kg) and (iii) the period of oscillation, if the body is left free. View SolutionQuestion 30
A spring compressed by 0.1m develops a restoring force 10N. A body of mass 4kg is placed on it. Deduce (i) the force constant of the spring (ii) the depression of the spring under the weight of the body ( take g=10N/kg) and (iii) the period of oscillation, if the body is left free. View SolutionQuestion 44
A lactometer whose mass is 0.2kg is floating vertically in a liquid of relative density 0.9. Area of cross-section of the mariked portion of lactometer in 0.5×10−4m2. If it is dipped down in the liquid slightly and released, what type of motion will it execute? what will be its time-period? View SolutionQuestion 77
Two bodies (M) and (N) of equal masses are suspended from two separate massless springs of spring constants (k_1) and (k_2) respectively. If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibration of (M) to the of (N) is.View SolutionQuestion 80
A massless spring of natural length of 0.5 m and spring constant 50 N/m has one end fixed and the other end attached to a mass of 250 g. The spring mass system is on a smooth floor. The mass is pulled until the length of the spring is 0.6 m and then released from rest. The kinetic energy of the mass when the length of the spring is 0.5 m isView SolutionQuestion 162
The relation between the acceleration a and displacement x of a particle executing SHM is a=−(p/q)y , where p and q are constant quantities. What will be the time period of oscillation of the particle ? If p is doubled and q is halved, then find the value of new time period of oscillation. View SolutionQuestion 165
Passage V) In SHM displacement, velocity and acceleration all oscillate simple harmonically with same angular frequency ω. Phase difference between any two is π2 except that between displacement and acceleration which is π.
v-t graph of a particle is SHM is as shown in figure Choose the wrong option.
 View Solution
View SolutionQuestion 189
Two bodies (M) and (N) of equal masses are suspended from two separate massless springs of spring constants (k_1) and (k_2) respectively. If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibration of (M) to the of (N) is.View SolutionQuestion 219
Two bodies (M) and (N) of equal masses are suspended from two separate massless springs of spring constants (k_1) and (k_2) respectively. If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibration of (M) to the of (N) is.View SolutionQuestion 225
The bob of a simple pendulum executm simple harmonic motion in water with a period t, while the period of oscillation of the bob is t0 in air. Negleting frictional force of water and given that the density of the bob is (4//3)xx1000 kg//m^(3).
What relationship between t and t0 is true.View SolutionQuestion 226
A cylindrical of wood (density =600kgm−3) of base area 30cm2 and height 54cm, floats in a liquid of density 900kg−3 The block is deapressed slightly and then released. The time period of the resulting oscillations of the block would be equal to that of a simple pendulum of length (nearly) :View SolutionQuestion 227
If a simple pendulum has significant amplitude (up to a factor of1//e of original) only in the period between t−0s→t=τs, then τ may be called the average life of the pendulum. When the sphetical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity with b as the constant of propotional to average life time of the pendulum is (assuming damping is small) in seconds:View SolutionQuestion 231
Two particles are in SHM in a straight line about same equilibrium position. Amplitude A and time period T of both the particles are equal. At time t=0, one particle is at displacement y1=+A and the other at y2=−A/2, and they are approaching towards each other. after what time they cross each other?View Solution