Unsolved Numerical from GK PUBLICATIONS PHYSICS Chapter 6 RIGID BODIES AND ROTATIONAL MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | RIGID BODIES AND ROTATIONAL MOTION |
| GK PUBLICATIONS PHYSICS | Unsolved Numerical |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
Two masses M and m are connect by a light string gong over a pulley of radis r. The pulley is free to rotate about its axis which is kept horizontal. The moment of inertia of the pulley about the axis is I. The system is releaed from rest. Find the angular momentum fo teh system when teh mass Mhas descended through a height h. The string does not slip over the pulley.View SolutionQuestion 2
A ball of radius R=10.0cm rolls without slipping down an inclined plane so that its centre moves with constant acceleration
w=2.50cm/s2, t=2.00s after the beginning of motion its position corresponds to that shown in figure. Find:
(a) the velocities of the points A, B, and O,
(b) the accelerations of these points.
 View Solution
View SolutionQuestion 6
A spool (consider it as a double disc system joined by a short tube at their centre) is placed on a horizontal surface as shown Fig. A light string wound several times over the short connecting tube leaves it tangentially and passes over a light pulley. A weight of mass m is attached to the end of the string. The radius of the connecting tube is r and mass of the spool is M and radius is R. Find the acceleration of the falling mass m. Neglect the mass of the connecting tube and slipping of the spool.
 View Solution
View SolutionQuestion 7
A midpoint of a thin uniform rod AB of mass m and length l is rigidly fixed to a rotation axle OO′ as shown in figure. The rod is set into rotation with a constant angular velocity ω. Find the resultant moment of the centrifugal forces of inertia relative to the point C in the reference frame fixed to the axle OO′ and to the end.
 View Solution
View SolutionQuestion 10
A solid uniform sphere, with radius R = 0.2 m and mass M=50kg,is at rest in an inertial reference frame in deep space. A bullet with mass w = 20 gm and a velocity v= 400 m/s strikes the sphere along the line shownin figufe-5.137, and rapidly comes to rest within the sphere at point P. Determine the subsequent motion of the sphere and the embedded bullet.
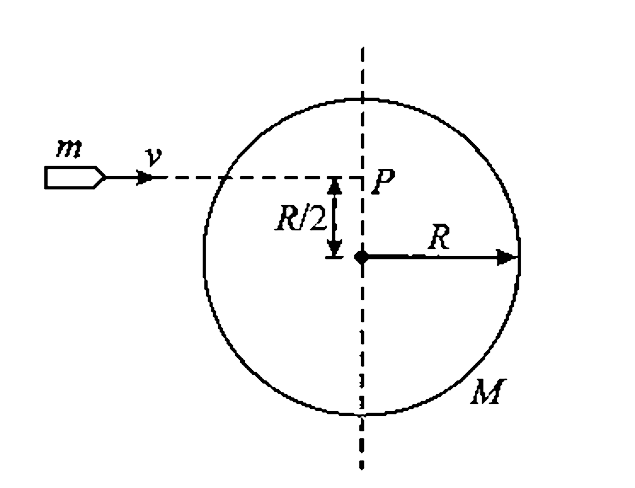 View Solution
View SolutionQuestion 11
In a spring gun, a spring of force constant 200N/mis compressed 0.15 m. When fired, 80% of the elastic potential energy stored in the spring is eventually converted into kinetic energy of a 0.1 kg uniform ball that is rolling without slipping at the base of a ramp. The ball continues to roll without slipping up the ramp with 90% of the kinetic energy at the bottom converted into an increase in gravitational potential energy at the instant it stops.
(a) What is the speed of the ball's centre ofmass at the base of the ramp
(b) At this position, what is the speed of a point at the top of the ball?
(c ) What maximum vertical height up the ramp does the ball move?View SolutionQuestion 13
(a) Compute the torque developed by an automotive engine whose output is 180 kW at an angular velocity of 4000rev/min. (b)A drum of negligible mass, 0.min diameter, is attached to the motorshaft,and the powerout put of the motor is used to raise a weight hanging from a rope wrapped around the drum. How large a weight can be liftd? Assume contant speed(c) With with what speed will the weigh rise?View SolutionQuestion 14
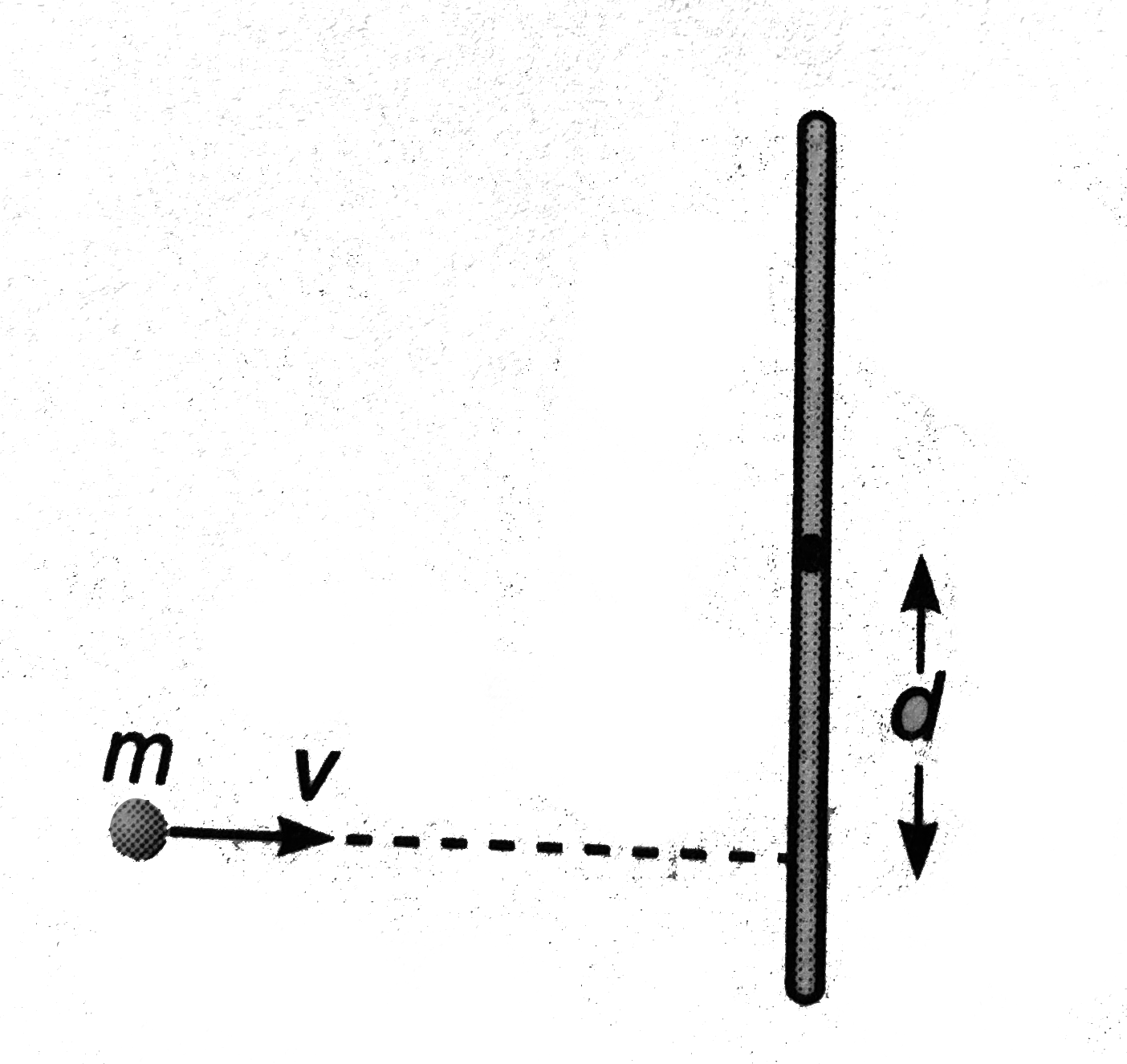
A stick of length l lies on horizontal table. It has a mass M and is free to move in any way on the table. A ball of mass m moving perpendicularly to the stick at a distance d from its centre with speed v collides elastically with it as shown in figure. What quantities are conserved in the collision ? what must be the mass of the ball, so that it remains at rest immediately after collision?View SolutionQuestion 15
A small steel sphere of mass m and radius r rolls without slipping on the fiictionless surface of a large hemisphere of radius R{R gt gt r) whose axis of symmetry is vertical. It starts at the top from the rest, (a) What is the kinetic energy at the bottom ? (b) What fraction is the rotational kinetic energy of the total kinetic energy at the bottom? (b) What fraction is the rotational kinetic energy of the total kinetic energy? (c) What fraction is the translational kinetic energy of the total kinetic energy? (d) Calculate the normal force that the small sphere will exerton.the hemisphere at its bottom. Howthe results will be affected if r is not very sjnall as compared to R.View SolutionQuestion 16
The carbide tips of the cutting teeth of a circulars aware 9.2 cm from the axis ofrotation, (a) The no-load speed of the saw,whenit is not cutting anything, is 5000 rev/min.Why is its no-load power output negligible ? (b) While cutting lumber, the angular speed of the saw slows to 2500 rev/min, and the power output is 2.1 hp. What is the tangential force that the wood exerts on the carbide tips.View SolutionQuestion 17
A uniform rod ofmassm and length / rests on a smooth horizontal surface. One of the ends ofthe rod is struck in'a horizontal direction at right angles to the rod. As a result the rod obtains velocity Vq. Findtheforcewithwhich onehalfof the rod will act on the other in the process ofmotion.View SolutionQuestion 18
A smooth uniform rod AB of mass M and length l rotates freely with an angular velocity ω0 in a horizontal plane about a stationary vertical axis passing through its end A. A small sleeve of mass m starts sliding along the rod from the point A. Find the velocity v′ of the sleeve relative to the rod at the moment it reaches its other and B. View SolutionQuestion 19
The fly wheel of a large motorin a factory has mass 30kg and moment of inertia 67.5kg−m2 about its rotation axis. The motor develops a constanttorque of 600N-m, and the fly wheel starts from rest, (a) What is the angular acceleration of the fly wheel ? (b) What is its angular velocity after making 4 revolutions ? (c) How much work is done by the motor during the first 4 revolutions ? (d) What is the average power output ofthe motor during the first 4 revolutions ?View SolutionQuestion 20
Figure-5.139 shows three identical kiting spools at rest on a rough horizontal groundinitially.In each case the string is pulled in the direction shown in figure. In each case it is given that spool rolls without slipping. In what direction will each spoolwill move and with what acceleration. Moment ofinertia ofeach spool is 7and radius of innertube is r and that ofouter disc is R.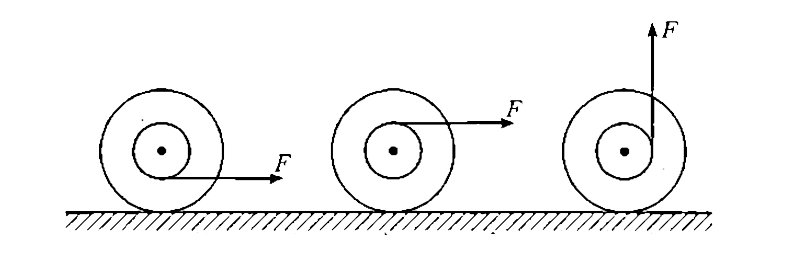 View Solution
View SolutionQuestion 21
A closed system consists of two particles of masses m1 and m2 which move at right angles to each other with velocities v1 and v2. Find:
(a) the momentum of each particle and
(b) the total kinetic energy of the two particles in the reference frame fixed to their centre of inertia.View SolutionQuestion 22
Two uniform thin rods A and B of length 0.6 m each and of masses 0.01 kg and 0.02kg respectively are rigidly joined end to end. The combination is pivoted at the lighter end, P as shown in fig. Such that it can freely rotate about point P in a vertical plane. A small object of mass 0.05kg, moving horizontally, hits the lower end of the combination and sticks to it what should be the velocity of the object so that the system could just be reised to the horizontal position.
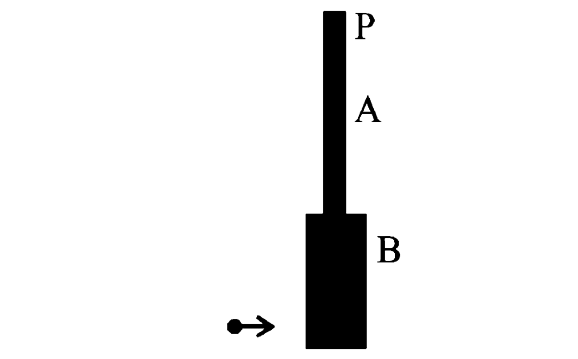 View Solution
View SolutionQuestion 25
A uniform thin rod of mass m and length L is standing vertically along the y-axis on a smooth horizontal surface, with its lower end at the origin (0,0). A slight disturbane at t = 0 causes the lower end t slip on the smooth surface along the positive x-axis, and the rod starts falling.
(i) What is the path followed by the centr of mass of the rod during its fall?
(ii) Find the equaiton to the trajectory of a point on the rod shape of the path of this point?View SolutionQuestion 26
A carpet of mass M is rolled along its length so as to from a cylinder of radius R and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to R/2.View SolutionQuestion 27
A small sphere of radius R is held against the inner surface of larger sphere of radius 6R (as shown in figure). The masses of large and small spheres are 4M and M respectivley. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the large spheres, when the smaller sphere reaches the other extreme position.
 View Solution
View SolutionQuestion 28
A vertically oriented uniform rod of mass M and length l can rotate about its upper end. A horizontally flying bullet of mass m strikes the lower end of the rod and gets stuck in it, as a result, the rod swings through an angle α. Assuming that m<<M, find:
(a) the velocity of the flying bullet,
(b) the momentum increment in the system "bullet-rod" during the impact, what causes the change of that momentum,
(c) at what distance x from the upper end of the rod the bullet must strike for the momentum of the system "bullet-rod" to remain constant during the impact. View SolutionQuestion 29
A Stick of length L and mass M lies on a fnctionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shownin figure-5.115. If after the collision ball comes to rest, then what should be the mass of the ball ?
 View Solution
View SolutionQuestion 30
A uniform solid cylinder of radius R=15cm rolls over a horizontal plane passing into an inclined plane forming an angle α=30∘ with the horizontal(figure). Find the maximum value of the velocity v0 which still permits the cylinder to roll onto the inclined plane section without a jump. The sliding is assumed to be absent.
 View Solution
View SolutionQuestion 31
A small spherical marble of mass m and radius r is rolling without slipping on a rough track with speed v.The track further is in the shape of a vertical circle of radius R as shown in figure-5.144. With what minimum linear speed the marble is rolling so that it completely goes round the circle on the circular part of track.
 View Solution
View SolutionQuestion 32
A horizontal rotating disc placed on arough surface has an angular speed of 8 rad/s when it is lowered on the surface. After 3 seconds, it is observed to have an angular speed of 2.6 rad/s. How many revolutions it made from the time of loweringon the surface until it stops ? Assume the pressure on the surface due to disc is uniform on its area.View SolutionQuestion 33
A thin horizontal uniform rod AB of mass m and length l can rotate freely about a vertical axis passing through its end A. At a certain moment, the end B starts experiencing constant force F which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. Find the angular velocity of the rod as a function of its rotation angle ϕ counted relative to the initial position.View SolutionQuestion 34
A disc of circumference S stands vertically on a horizontal surface as shown in figure-5.145, A horizontal force P acts on the centre of the disc. Half of the circumference {ABC) is rough and the friction is sufficient to prevent slipping when the disc rolls along X¥.The other half of the circumference (ADC) is smooth. The disc starts from rest when P begins to act and the point C is at the bottom. Find the distance moved by the disc along xy when it completes one rotation.
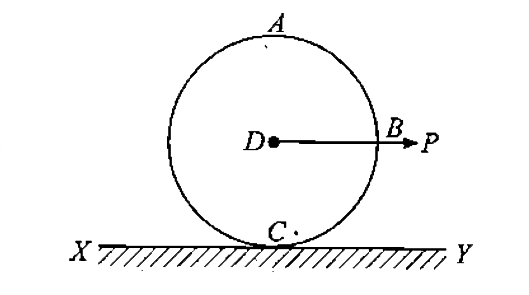 View Solution
View SolutionQuestion 35
A block of mass m1 =2 kg slides along a firictionless table with a speed of 10m/s. Directly infront of it,and moving in the same direction is a block of mass m2 5 kg moving at 3 m/s. A mass less spring with a spring constant 11.2 N/cm is attached to as shown in figure-5.146. When the block collide,what is the maximum compression of the spring ? Assume that the spring does not bend.
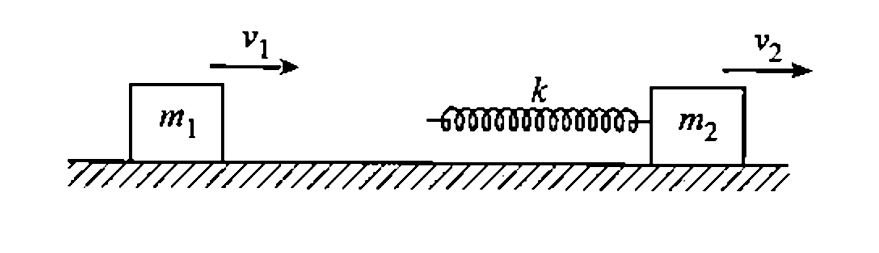 View Solution
View SolutionQuestion 38
Discs A and B are mounted on a shaft XY and may be connected or disconnected by a coupling Z as shown in figure-5.147. The moment of inertia of disc A about the shaft is half that of disc B. The moments of inertia of the shaft and the coupling are negligible. Initially A is disconnected and rotated at an angular velocity ω. It is now coupled to disc B using couplings.It is found that 5000 J of thermal energy is developed in the coupling when the connection is made. What was the original kinetic energy of the disc A.
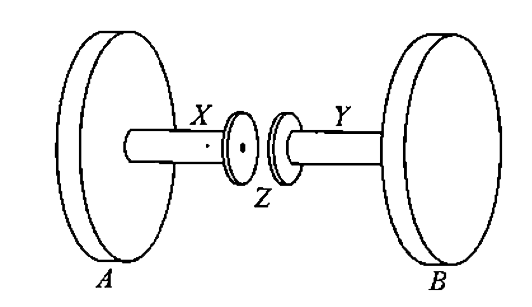 View Solution
View SolutionQuestion 39
A spool with thread wound on it, of mass m, rests on a rough horizontal surface. Its moment of inertia relative to its own axis is equal to I=γmR2, where γ is a numerical factor, and R is the outside radius of the spool. The radius of the wound thread layer is equal to r. The spool is pulled without sliding by the thread with a constant force F directed at an angle α to the horizontal (figure). Find:
(a) the projection of the acceleration vector of the spool axis on the x-axis,
(b) the work performed by the force F during the first t seconds after the beginning of motion.
 View Solution
View SolutionQuestion 40
A small body of mass m tied to a non-stretchable thread moves over a smooth horizontal plane. The other end of the thread is being drawn into a hole O(figure) with a constant velocity. Find the thread tension as a function of the distance r between the body and the hole if at r=r0 the angular velocity of the thread is equal to ω0.
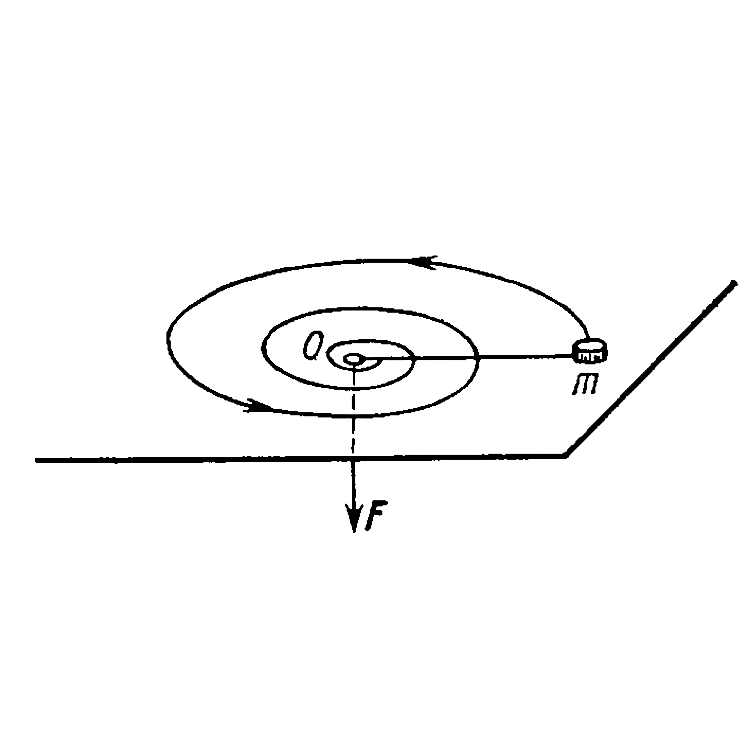 View Solution
View SolutionQuestion 41
A ball ofmass m moving with velocity experiences a head on elastic collision with one of the spheres of as tationary rigid dumbbell as shown in figure-5.149. The mass of each sphere equals m/2, and the distance between them is l.Disregarding the size of the spheres, find the angular momentum of the dumbbell in the reference frame moving translationally and fixed to the centre of mass of the dumbbell.
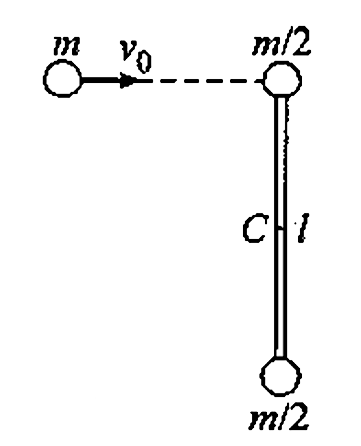 View Solution
View SolutionQuestion 42
A spool has a mass of 2 kg,an inner radius R1 =3cm,and an outer radius R2=5cm, the radius of gyration about the axis of the spool is if=4cm.A constant horizontal force of 5N is applied to the free end of a massless thread that is wrapped around the inner cylinder of the spool as shownin figure-5.150. If the spool rolls without slipping, calculate the linear acceleration along the horizontal surface. What is the minimum coefficient of static friction required to prevent slipping ?
 View Solution
View SolutionQuestion 43
A homogeneous disc of weight W and radius R rotates about the vertical axis OZ, the initial angular velocity being ω0. During the motion, the brake block A is pressed to the disc,with a radial force N for t0 seconds and the disc comes to rest because of friction. Find the coefficient of friction.View SolutionQuestion 44
A uniform disc of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts with a purely sliding motion at t= 0. After t0 seconds it acquires a purely rolling motion.
(a) Calculate the velocity of the centre of mass of the disc at t0
(b) Assuming the coefficient of friction to be μ, calculate to. Also calculate the work done by the frictional force as a function of time and the total work done by it over a time t muchlonger than t0. View SolutionQuestion 45
A uniform rod AB of mass m=2kg and length l=1.0m is placed on a sharp support P such that a=0.4m and b=0.6m. A. spring of force constant k=600N/m is attached to end B as shown in Fig. To keep the rod horizontal, its end A is tied with a thread such that the spring is B elongated by 1CM. Calculate reaction of support P when the thread is burnt.
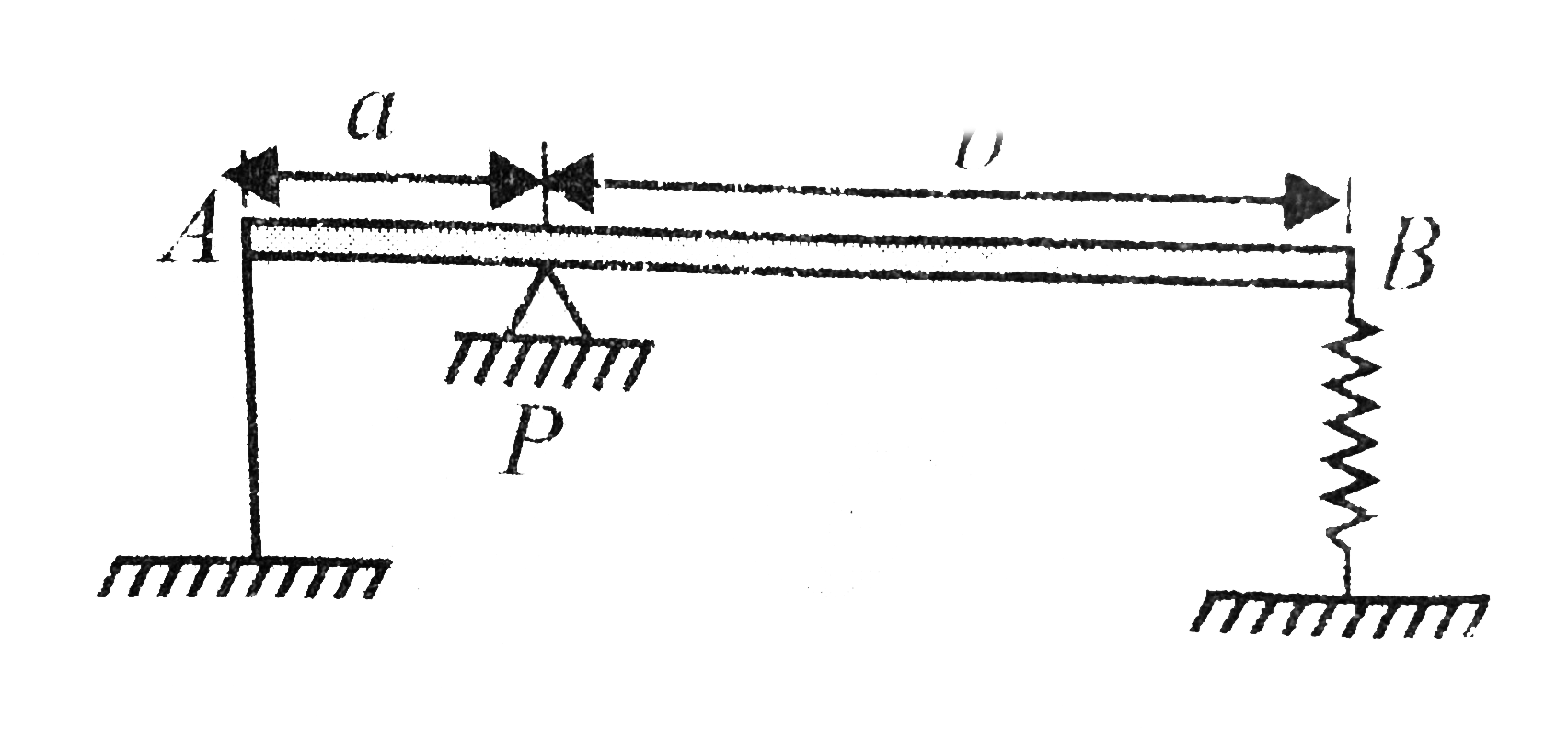 View Solution
View SolutionQuestion 46
A small ball is suspended from a point O by a light thread of length l. Then the ball is drawn aside so that thread deviates through an angle θ from the vertical and set in motion in a horizontal direction at right angles to the vertical plane in which the thread is located. What is the initial velocity that has to be imparted to the ball so that it could deviate through the maximum angle π/2 in the process of motion? View SolutionQuestion 47
An object rotates about a fixed axis, such that a reference line on the object makes an angle θ=aebt with its starting position at time t. Find for a particle on object at a distance r from the axis of rotation, the tangential, the radial and the total acceleration of the point. View SolutionQuestion 48
A rectangular rigid fixed block has a long horizontal edge. A solid homogeneous cylinder of radus R is placed horizontally at rest its length parallel to the edge such that the exis of the cylinder and the endg of the block are in the same vertical plane as shown in the figure below. Ther is sufficinet friction present at the edge s that a very small displacement causes the cylinder to roll off the edge without slipping. Determine:

(a) the angle θc through which the cylinder rotates before it leaves contact with the edge,
(b) the speed of the centre of mass of the cylinder before leaving contact with the edge, and
(c) the ratio of the translational to rotational kinetic energy of the cylinder when its centre of mass is in horizontal line with the edge.View SolutionQuestion 49
A 392 N wheel comes off a moving truck and rolls without slipping along a highway. At the bottom of a hill it is rotating at 50 rad/s. The radius ofthewheel is 0.6m, and its moment of inertia about its rotation axis is 0.8MR2. Friction does 3000 J of work on the wheel as it rolls up the hill to a stop a height h above the bottom of the hill. Calculate h.View SolutionQuestion 50
A grindstone in the form of a solid cylinder has a radius of 0.2m and a mass of 30 kg. (a)What constant torque will bring it from rest to an angular velocity of 250 rev/min in 10 s ?
(b) Through what angle has it turned during that time ?
(c) Calculate the work done by the torque.View SolutionQuestion 51
A constant net torque equal to 20 N-m is exerted on a pivoted wheel for 8 sec, during which time the angular velocity of the wheel increases from zero to 100 re/min. The external torque is then removed and the wheel is brought to rest by friction in its bearings in 70 sec. Compute (a) the moment of inertia of the wheel about the rotation axis, (b) the friction torque(c)thetotal no. of revolutions made by the wheel in the70 sec time intervalView SolutionQuestion 52
In the arrangement shown in figure a weight A possesses mass m, a pulley B possesses mass M. Also known are the moment of inertia I of the pulley relative to its axis and the radii of the pulley R and 2R. The mass of the threads is negligible. Find the acceleration of the weight A after the system is set free.
 View Solution
View SolutionQuestion 53
A solid spherical ball of radius 30 cm and mass M is connected to a point A on wall with a thread and freely rotate about its central axis with angular velocity 60 rad/sec. If the ball is resting onthe vertical face of a wall, what time will elapse before it comes to rest ? The coefficient of friction between wall and ball is 0.25 and inclination of thread to vertical is 15∘.View SolutionQuestion 54
A thin uniform rod of mass m and length l rotates with the constant angular velocity ω about the vertical axis passing through the rod's suspension point O. In doing so, the rod describes a conical surface with a half separated angle θ.Find the angle θ as well as the magnitude and direction of the reaction force at the point O.View SolutionQuestion 56

Consider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll the plank always remains horizontal. there is no slipping at any point of contact. Calculate the acceleration of the cylinder and the frictional forces at the two contact.View SolutionQuestion 58
The mechanism shown in figure-5.156 is used to raise a wooden box of mass 50kg .A string is wrapped around a cylinder that turns on an axle.The cylinder has radius 0.25 m and moment of inertia 0.92 kg−m2 about the axle. What magnitude of the force F applied tangentially to the rotating crank handle is required to raise the box with an acceleration of 0.80m/s.Here we can neglect the moment of inertia of the axle and the crank
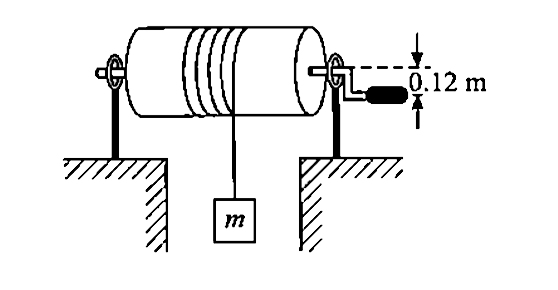 View Solution
View SolutionQuestion 59
A uniform spherical shell of mass M and radius R rotates, about a vertical axis on frictionless bearing. A massless cord passes around the equator of the shell., over a pulley of rotational inertia I and radius r and is attached to small object of mass m that is otherwise free to fall under the influence of gravity. There is no friction of pulley's axle, the cord does not slip on the pulley. What is the speed of the object after it has fallen a distance h. from rest? Use work-energy considerations.
 View Solution
View SolutionQuestion 61
Two wooden disc , one with radius 2 cm and mass 1 kg and the other with radius 4 cm and mass 2 kg , are welded together coaxially and mounted on a frictionless axis through their common centre. Alight string is wrapped around the edge of the smaller disc, and a 3 kg block is suspended from the free end of the string.What is the acceleration of the block after it is released? Repeat the above process if the stringi swrapped around the edge of the larger disc.View SolutionQuestion 62
A horizontal wooden disc of mass 8 kg and diameter 1m is pivoted on frictionless bearing about a vertical axis through its centre.We put a toy train track model in the disc.The track has a negligible mass and average diameter 0.95 ra.The mass ofmodel train is 1.2 kg which can run with a battery.When we switch on the engine the train moves anticlockwise, soon attaining a constant speed of 0.6 m/s with respect to the track. Find the magnitude and direction of the angular velocity of the disc relative to the earth.View SolutionQuestion 63
A 50 kg runner runs around the edge of a turn table mounted on frictionless bearings. With respect to earth the velocity of runner is 2m/s.The turntable is rotating in opposite direction with an angular velocity of magnitude 0.2 rad/s with respect to earth.The radius of turntable is 4m, and its moment of inertia is 1000 kg−m2. Find the final angular velocity of the system if runner comes to rest relative to turntable.View Solution