A spool with thread wound on it, of mass m, rests on a rough horizontal surface. Its moment of inertia relative to its own axis is equal to I=γmR2, where γ is a numerical factor, and R is the outside radius of the spool. The radius of the wound thread layer is equal to r. The spool is pulled without sliding by the thread with a constant force F directed at an angle α to the horizontal (figure). Find:
(a) the projection of the acceleration vector of the spool axis on the x-axis,
(b) the work performed by the force F during the first t seconds after the beginning of motion.

The correct Answer is:⎡⎢ ⎢⎣F(cosθ−rR)m(1+γ),F2t2(cosθ−rR)2m(1+γ)⎤⎥ ⎥⎦
Step by step video, text & image solution for A spool with thread wound on it, of mass m, rests on a rough horizontal surface. Its moment of inertia relative to its own axis is equal to I=gammamR^2, where gamma is a numerical factor, and R is the outside radius of the spool. The radius of the wound thread layer is equal to r. The spool is pulled without sliding by the thread with a constant force F directed at an angle alpha to the horizontal (figure). Find: (a) the projection of the acceleration vector of the spool axis on the x-axis, (b) the work performed by the force F during the first t seconds after the beginning of motion. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - MCQ
16 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Video
Similar Questions
A spool of inner radius R and outer radius 3R has a moment of inertia =MR2 about an axis passing through it's geometric centre, where M is the mass of the spool. A thread wound on the inner surface of the spool is pulled horizontally with a constant force =Mg. Find the acceleration of the point on which is being pulled assuming that the spool rolls purely on the floor.
 .
.
View SolutionA bar of mass m is pulled by means of a thread up an inclined plane forming an angle α with the horizontal (figure). The coefficient of friction is equal to k. Find the angle β which is thread must form with the inclined plane for the tension of the thread to be minimum. What is it equal to?

View Solution
Knowledge Check
A solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is ?
AMR22BMR2C32MR2D2MR2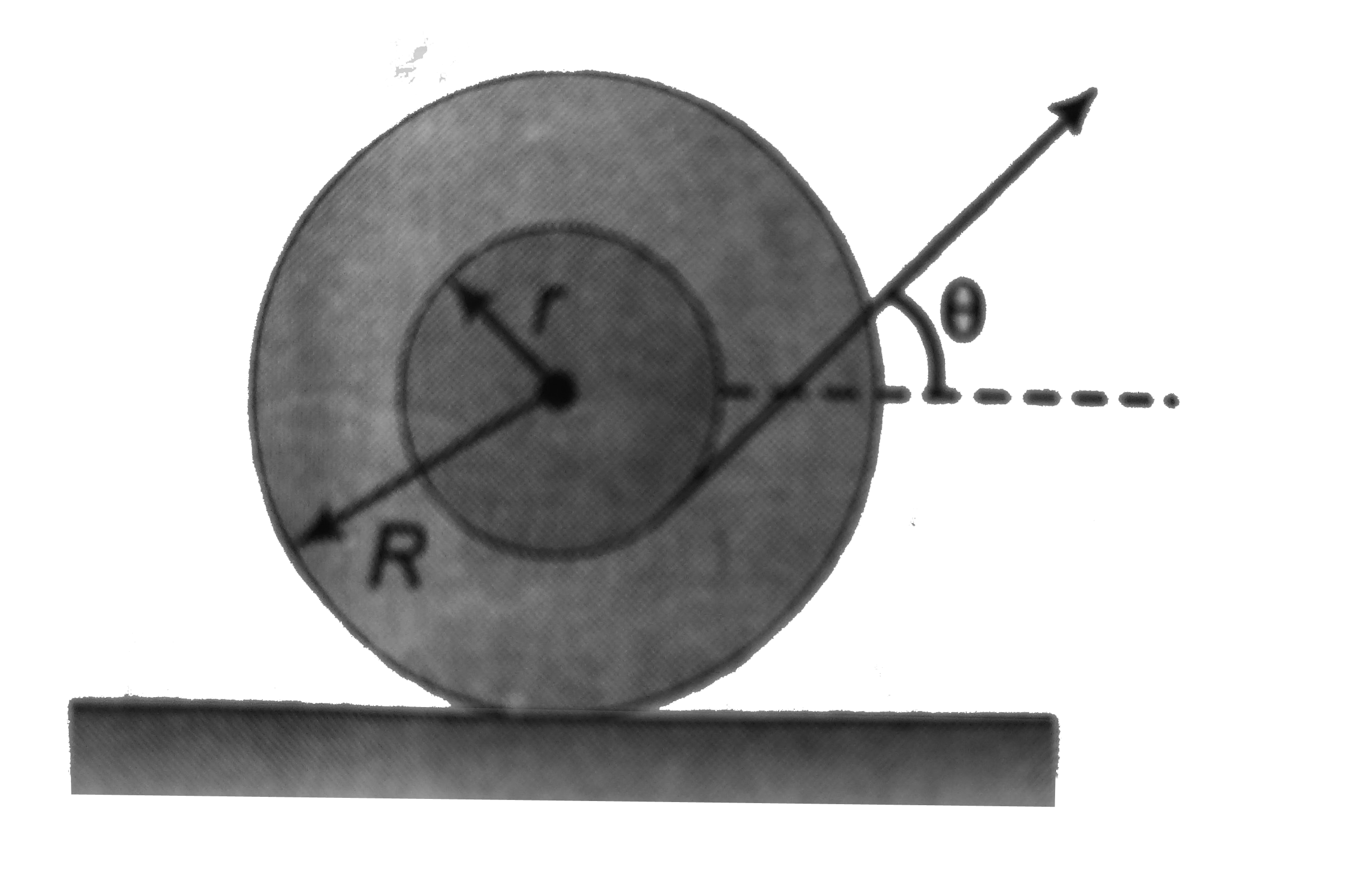
A spool is pulled at an angle θ with the horizontal on a rough horizontal surface as shown in the figure. If the spool remains at rest, the angle θ is equal toAcos−1(Rr)Bsin−1(√1−r2R2)Cπ−cos−1(rR)Dsin−1(rR)If the moment of inertia of a rigid body is numerically equal to its mass, radius of gyration is
Aequal to its radiusBequal to diameterCequal to one unitDinfinite
A spool with a thread wound on it is placed on an inclined smooth plane set an angle α=30∘ to the horizontal. The free end of the thread is attached to the wall as shown in figure. The mass of the spool is m=200g, its moment of inertia relative to its own axis I=0.45g⋅m2, the radius of the wound thread layer r=3.0cm. Find the acceleration of the spool axis.
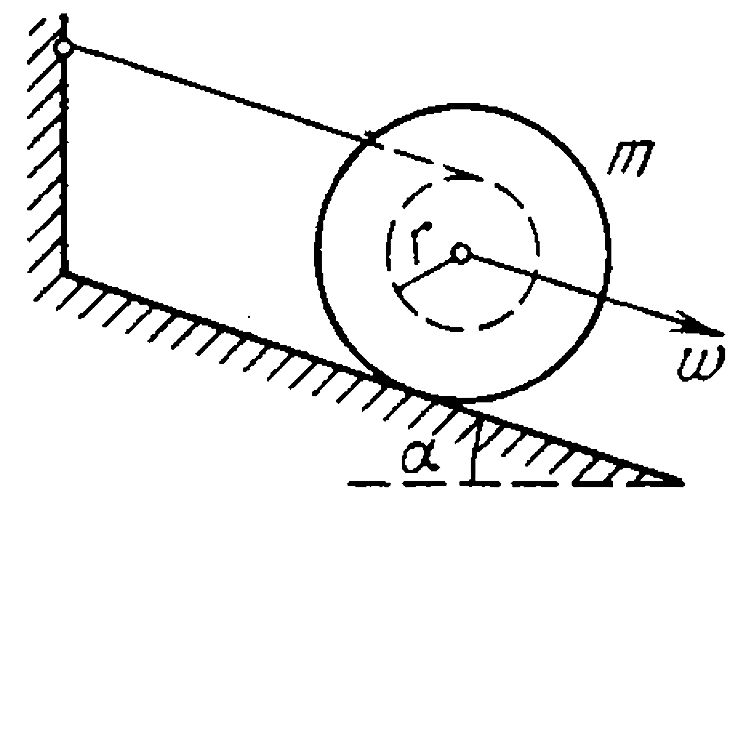
View SolutionA spool with a thread wound on it is placed on a smooth inclined plane set at an angle of 30 to the horizontal. The free end of the thread is attached to the wall as shown. The mass of the spool is m r m 200g, its moment of inertia relative to its own axis is I 0.45gm2, the radius of the wound thread layer is r 3 cm. The acceleration of the spool axis is:

View SolutionA uniform cylinder of mass m rests on two rough horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F
View SolutionThe relation between length L and radius R of the cylinder , if its moment of inertia about its axis is equal to that about the equatorial axis, will be
View SolutionA uniform disc of radius R lies in x-y plane with its centre at origin. Its moment of inertia about the axis x=2R and y=0 is equal to the moment of inertia about the axis y=d and z=0, where d is equal to
View Solution